AGC073

https://atcoder.jp/contests/agc073/tasks/agc073_a

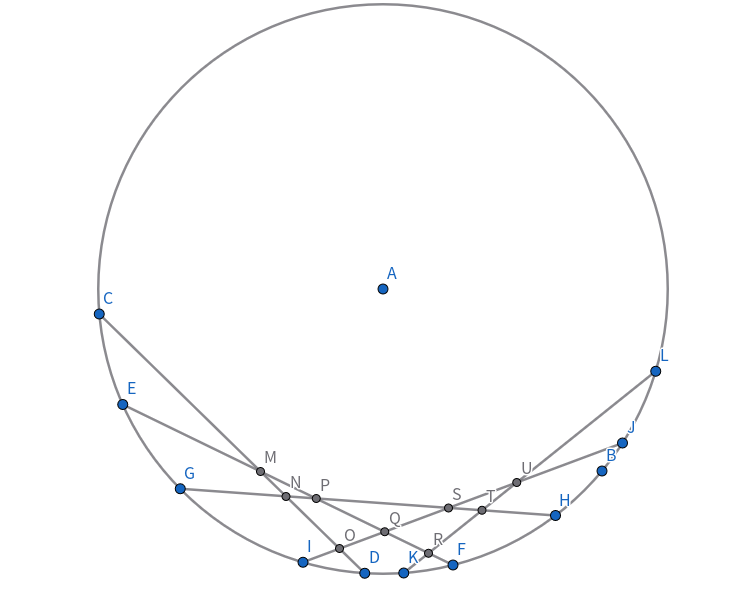
考虑这么一个图，我们考虑最外层的一层框，如图中的 \(C,M,P,S,U,L\) 边框，对于线段 \(PS\)，我们计算 \(PFH\) 这个区域黑色区域的数量，首先 \(PS\) 是弦 \(GH\) 的一部分，进而发现每一条起点介于 \(G,H\) 之间的弦都会时区域数增加 \(1\)，而与其他因素无关，直接做即可。

https://atcoder.jp/contests/agc073/tasks/agc073_b

一个简单的想法是可以选择 \(a_1,a_2\)，然后能得到一个 \(a_1+a_2\) 的解。但这没什么用，考虑先取个 \(a_1\)，先走 \(+a_1\)，把其他数全部减 \(a_1\)，这样变成了一个更小的子问题，一直做下去，相当于辗转相除。每次取最小值。

https://atcoder.jp/contests/agc073/tasks/agc073_c

枚举 \(x\)，看看计算出一个给定的 \(x\) 的概率。对于一条边，考虑断掉它后两个端点的 \(x\) 分别为 \(a,b\)，如果 \(a>0,b>0\) 则合并后两个端点的 \(x\) 都变为 \(a+b\)，然后分析一下，如果 \(x\) 全相等，设其为 \(k\)，考虑微元法，转为在 \([-(n-1)\Delta,\Delta]\) 之间随机整数，然后相当于是说每个子树的权值和都在 \([0,\Delta k]\) 之间，进而可以唯一确定每个点的权值，方案数为 $\sum\limits_{0\le k\le \Delta k^{2n-1}} $，概率为 \(\frac {1}{n^n \Delta^{2n}}\)，在 \(\Delta \to \infty\) 时为 \(\frac{1}{2n}\)，进而对于 \(x\) 不全相等的情况，把 \(x\) 相同的部分缩成连通块，\(x\) 不相同的部分看起来可以构造双射，大力猜测互不影响，简单树形 dp 即可。