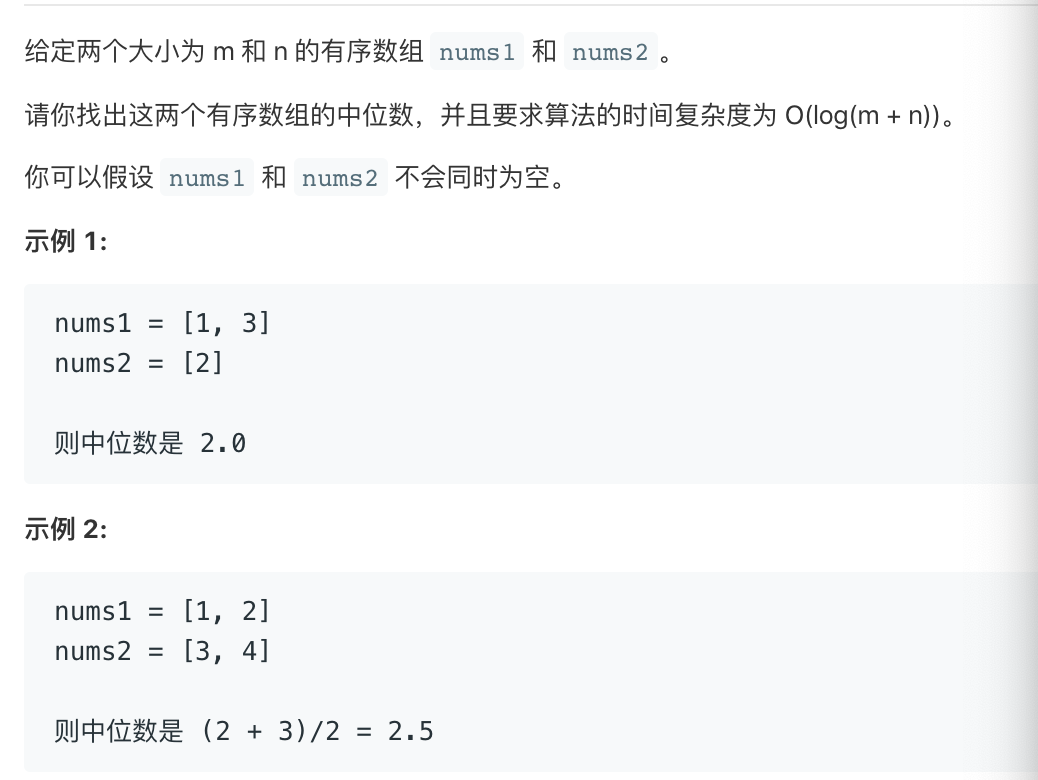
leetcode 每日一题 4.寻找两个有序数组的中位数

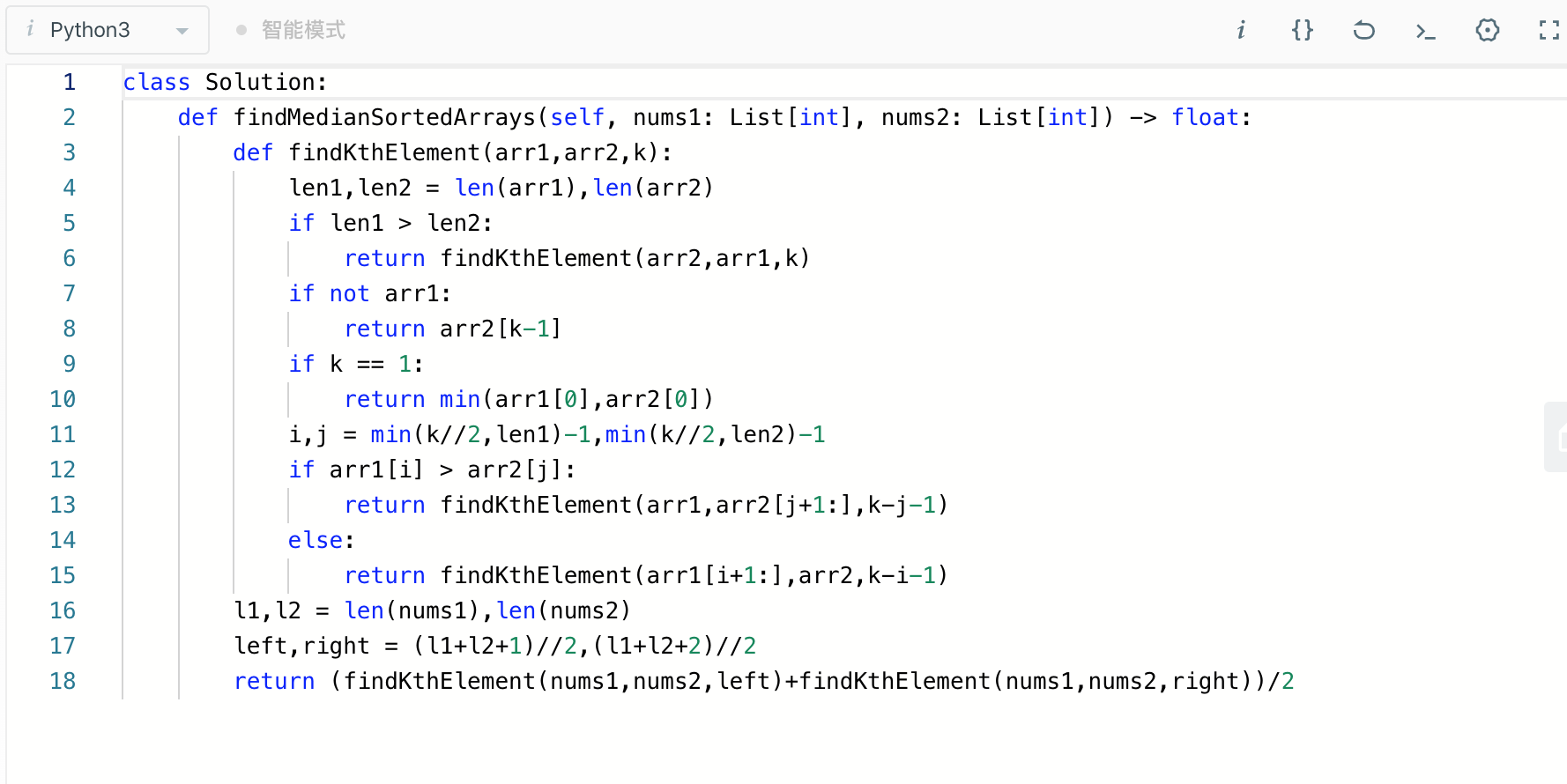
代码:

思路:

中位数首先要考虑数组长度奇偶性问题，如果数组长度n是奇数，则中位数为数组第(n//2+1)个数。如果长度n为偶数，则中位数为数组第n//2个数和（n//2+1）个数的平均数。

 

例如：

[1,3,5]  中位数为第（3//2+1）=2个数，即3

[1,3,4,5] 中位数为第（4//2）=2个数即3 和第（4//2+1）=3个数即4 的平均数即  （3+4）/2 = 3.5

 

寻找长度为m的数组nums1和长度为n的数组nums2的中位数，可以先将两个数组排序后成为一个（m+n）大小新的有序数组，再取新数组的中位数k即可。但采用此种方法时间复杂度为O（m+n），无法满足题目要求O（log（m+n）），因此不能采用将两个数组合并排序的方法。

 

假设两个数组的中位数在（m+n）大小合并有序数组中的位置为k，则题目等价于寻找两个有序数组中第k小的数。由于长度奇偶性的原因，这里k的位置需要分情况讨论：

如果 （m+n）是奇数，则k=（m+n）//2+1，只需要寻找第k小的数即可 ；

如果（m+n）是偶数，则k1=(m+n)//2，k2=(m+n)//2+1，需要寻找第k1小的数和第k2小的数，再将两者取平均数；

两种情况统一处理，k1 = (m+n+1)//2，k2 = (m+n+2)//2，寻找第k1小和第k2小的数，取平均值；

例如：

偶数:   [3,5,6]  , [4,7,8]  k1 = 7//2 = 3 , k2 = 8//2 = 4, 第三小的数为5,第四小的数为6,平均数为 (5+6)/2=5.5;

奇数:   [3,5,6] ，[4,7] k1 = 6//2 = 3, k2 = 7//2 = 3, 第三小的数为5,第三小的数为5, 平均数为(5+5)/2= 5;

 

则代码为:

def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:
    l1,l2 = len(nums1),len(nums2)
    left,right = (l1+l2+1)//2,(l1+l2+2)//2
    return (findKthElement(nums1,nums2,left)+findKthElement(nums1,nums2,right))/2    //(findKthElement函数为查找第k个小的数)

 

 

        

接下来讨论如何从两个有序数组arr1和arr2中获得第k小的数

 

首先，为了方便，我们将长度较短的一个数组置为arr1，长度较长的数组置为arr2；

 

接下来分情况讨论：(因为数组下标从0开始,涉及到数组第k个数时,在数组中的位置为arr[k-1])

 

1. 如果arr1为空，则直接返回arr2中第k个数即可

例如:  arr1 = []  arr2 = [4,5,6]   k = 2   则返回arr2第2个数 即 arr2[2-1]= 5 

               

2.如果arr1不为空且k=1，因为两个数组为有序数组，故只需要比较两个数组第一位数值大小，返回最小的数即可；

例如: arr1= [1,4,5] arr2 = [2,3,6] k = 1  则返回arr1[1-1] = 1 ,arr2 [1-1] = 2 两者的较小值 1 

 

3.如果上面1，2条件都不满足,则对两个数组进行递归切分剪枝处理,直到满足1，2条件为止

 

下面讨论如何对数组进行切分剪枝处理:

       

思路:

用二分法思想，对arr1和arr2各取第k//2个数进行讨论  a = arr1[k//2-1]   b = arr2[k//2-1]

(这里可能会出现数组长度少于k//2个的情况，出现少于的情况时直接取数组最后一个数即可)    

如果a > b，则将arr2中b位置后面的子数组切出来同arr1进行取最小数操作，同时k的数值需要减去arr2中切掉的子数组中的元素个数

如果a < b，则将arr1中a位置后面的子数组切出来同arr2进行取最小数操作，同时k的数值需要减去arr1中切掉的子数组中的元素个数

     例如：

以  arr1 = [4,6,7,9]  arr2 = [1,2,3,5,8,10,11]   k = 6   为例

 

① k//2=3,取 a = arr1[3-1] = 7 , b = arr2[3-1] = 3 ,

a>b ,所以此时 arr1 = [4,6,7,9] arr2 = [5,8,10,11]  k = 6-3 = 3

          ②k//2=1,取 a = arr1[1-1] = 4 , b = arr2[1-1] = 5 ,

a<b ,所以此时 arr1 = [6,7,9] arr2 = [5,8,10,11]  k = 3-1 = 2

③k//2=1,取 a = arr1[1-1] = 6 , b = arr2[1-1] =  5,

a>b ,所以此时 arr1 = [6,7,9] arr2 = [8,10,11]  k = 2-1=1

④此时k=1,故只需要比较arr1和arr2第一个元素大小返回较小值,即arr1[0] = 6 ,arr2[0] = 8,返回6

 

则查找第k个最小数函数代码为:

def findKthElement(arr1,arr2,k):
    len1,len2 = len(arr1),len(arr2)
    if len1 > len2:
        return findKthElement(arr2,arr1,k)
    if not arr1:
        return arr2[k-1]
    if k == 1:
        return min(arr1[0],arr2[0])
    i,j = min(k//2,len1)-1,min(k//2,len2)-1
    if arr1[i] > arr2[j]:
        return findKthElement(arr1,arr2[j+1:],k-j-1)
    else:
        return findKthElement(arr1[i+1:],arr2,k-i-1)

完整代码：

class Solution:
    def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:
        def findKthElement(arr1,arr2,k):
            len1,len2 = len(arr1),len(arr2)
            if len1 > len2:
                return findKthElement(arr2,arr1,k)
            if not arr1:
                return arr2[k-1]
            if k == 1:
                return min(arr1[0],arr2[0])
            i,j = min(k//2,len1)-1,min(k//2,len2)-1
            if arr1[i] > arr2[j]:
                return findKthElement(arr1,arr2[j+1:],k-j-1)
            else:
                return findKthElement(arr1[i+1:],arr2,k-i-1)
        l1,l2 = len(nums1),len(nums2)
        left,right = (l1+l2+1)//2,(l1+l2+2)//2
        return (findKthElement(nums1,nums2,left)+findKthElement(nums1,nums2,right))/2