简单数论与简单博弈论

数论博弈论

目录

• 数论博弈论
  • 上下取整问题
  • 关于ax+by的结论以及证明
  • 九余数定理
  • 秦九韶算法
  • 质数
    • 一、试除法判定质数
    • 二、分解质因数
    • 三、筛质数(筛法)
  • 约数
    • ①.试除法求约数
    • ②.约数个数
    • ③.约数之和
    • ④.最大公约数(欧几里得算法(辗转相除法))
  • 欧拉函数
  • 快速幂
  • 拓展欧几里得算法
  • 中国剩余定理
  • 高斯消元
  • 组合数
  • 容斥原理
  • 博弈论

上下取整问题

\[\begin{align} &\lceil \frac{a}{b} \rceil =\lfloor \frac{a+b-1}{b}\rfloor \\ &(a>0, b>0) \end{align} \]

证明：

a<b时证明较为容易不在此处提供。

关于ax+by的结论以及证明

\[\begin{align} &1.求ax+by的最大不能表示的数c，且满足x>0，y>0，则c=a*b\\ &2.求ax+by的最大不能表示的数c，且满足x>=0，y>=0，则c=a*b-a-b，且个数为(a-1)(b-1)/2\\ &上述结论的前提a,b互质（a,b为正整数） \end{align} \]

这里给出2的证明，1的证明与之类似，后期补充完整。

反证法：假设c=ab-a-b能够被ax+by表示，则ax+by=ab-a-b，则移项合并得a(x+1)+b(y+1)=ab，因为x,y>=0，所以x+1，y+1>=1.

设m=x+1，n=y+1，得m，n>=1，则am+bn=ab，因为ab是a得倍数，am也是a的倍数，即a|am，a|ab，所以想要算式成立，

则需要a|bn，因为a，b互质，所以需要a|n，即n是a的倍数，那么n>a，那么nb>ab，那么am+bn>ab，则假设不成立。

证明了不可以被表示之外还需要证明>ab-a-b的数字一定可以被表示

即需要证明ax+by=ab-a-b+i（i>=1）

因为a，b互质，所以gcd(a，b)=1，则根据裴属定理可得ma+nb=1，假设m>0，n<0，ab-a-b+i(ma+nb) ----> ab-a-b+ima+inb

-----> (im-1)a+(a-1+in)b，根据i>=1，m>0可得im-1>0，只需要再证明出a-1+in>=0即可. ima+inb=i ---> ima=i-inb, 因为i>=1，b>0

n<0，所以inb<0，那么ima=i+|inb|，

必要性证明请参照数论：px+py 不能表示的最大数为pq-p-q的证明 - PIPIBoss - 博客园 (cnblogs.com)

暂时上方的必要性证明没有证明出来,简单查了一下也没看懂

九余数定理

一个数对9取余后的结果成为九余数

一个数每一位上的数字之和相加后的结果<10的数字称为这个数的九余数(如果每一位相加后>10，则继续拆分每一位继续相加)

和的模 等于 模的和再取模 (15+7)%9 = (15%9+7%9)%9

积的模 等于 模的积再取模 (157)%9 = (15%97%9)%9

所以由此可以得到一个数字每一位上的数相加后的结果(<10)等于该数字对9趋于的结果

\[\begin{align} &证明如下：\\ &\quad\quad\quad\quad 假设有一个数字A，共有n位，每一位上的数字为a_i，则数字A=\sum_{i=0}^{n-1}{a_i*10^i}\\ &\quad\quad\quad\quad \because 10^n \equiv 1^n \equiv 1\ mod\ 9\\ &\quad\quad\quad\quad \therefore A \equiv \sum_{i=0}^{n-1}{a_i} \ mod \ 9\\ &\quad\quad\quad\quad 由此得证 \end{align} \]

秦九韶算法

针对于一元n次多项式的计算的优化

\[\begin{align} &f(x)=a_nx^n+a_{n-1}x^{n-1}+…………+a_2x^2+a_1x+a_0\\ &\quad\quad =(a_nx^{n-1}+a_{n-1}x^{n-2}+…………+a_2x+a1)x+a_0\\ &\quad\quad =((a_nx^{n-2}+a_{n-1}x^{n-3}+…………+a_2)x+a_1)x+a_0\\ &\quad\quad\quad...\\ &\quad\quad =(……((a_n+a_{n-1})x+a_{n-2})x+……+a_1)x+a_0\\ \end{align} \]

质数

质数定义:因子只包含1和其本身的数,称为质数.

一、试除法判定质数

\[\begin{align} &例:判断a是否是质数\\ &\because d|a\quad \therefore \frac{a}{d}|a\\ &并且这两个约数一定位于\sqrt{a}两边，所以仅需要遍历区间[2,\sqrt{a}]，判断是否有约数.\\ &若存在约数，则该数字为合数，若不存在则该数字为质数. \end{align} \]

/*
给定 n 个正整数 ai，判定每个数是否是质数。
输入格式
第一行包含整数 n。
接下来 n 行，每行包含一个正整数 ai。
输出格式
共 n 行，其中第 i 行输出第 i 个正整数 ai 是否为质数，是则输出 Yes，否则输出 No。
数据范围
1≤n≤100,
1≤ai≤2^31−1
输入样例：
2
2
6
输出样例：
Yes
No
*/
#include <iostream>
using namespace std;
int n;
bool isprime(int x);

int main()
{
    cin>>n;
    while(n--)
    {
        int a;
        cin>>a;
        if(isprime(a))
            puts("Yes");
        else
            puts("No");
    }
    
    return 0;
}
bool isprime(int x)
{
    if(x<2)
        return false;
    for(int i=2;i<=x/i;++i)//遍历[2,sqrt(x)]区间判断是否有多的约数
    {
        if(x%i==0)
        {
            return false;
        }
    }
    return true;
}

二、分解质因数

\[\begin{align} &定理:任意一个正整数n，至多只存在一个大于\sqrt{n}的质因子.\\ &证明:反正法\\ &假设有两个大于\sqrt{n}的质因数p_1,p_2.\\ &n>p_1*p_2>(\sqrt{n})^2=n\\ &\because n>n矛盾，所以假设不成立.\\ &\therefore 遍历区间[2,\sqrt{n}]，寻找质因子，最后在判断是否存在大于\sqrt{n}的质因子.\\ &此处有两种选择，一是体现构造好素数表去找在区间[2,\sqrt{n}]，并且能被整数的素数.\\ &二是直接循环遍历区间[2,\sqrt{n}]，由于1刚进入循环第一轮为质数2，第二轮为质数3，\\ &并且在找到约数的时候就将其进行n/(约数)的操作,那么前面的两轮可以保证将一些是合数的约数删去.\\ &在内循环中不能被整除.\\ \end{align} \]

/*
给定 n 个正整数 ai，将每个数分解质因数，并按照质因数从小到大的顺序输出每个质因数的底数和指数。
输入格式
第一行包含整数 n。
接下来 n 行，每行包含一个正整数 ai。
输出格式
对于每个正整数 ai，按照从小到大的顺序输出其分解质因数后，每个质因数的底数和指数，每个底数和指数占一行。
每个正整数的质因数全部输出完毕后，输出一个空行。
数据范围
1≤n≤100,
1≤ai≤2×109
输入样例：
2
6
8
输出样例：
2 1
3 1

2 3

*/
#include <iostream>
using namespace std;
void divide(int n);

int main()
{
    int n;
    cin>>n;
    while(n--)
    {
        int a;
        cin>>a;
        divide(a);
    }
    return 0;
}

void divide(int n)
{
    for(int i=2;i<=n/i;++i)
    {
        if(n%i==0)
        {
            int s=0;
            while(n%i==0)//此处保证较小的质数全部除去,不会存在多余质因子构成合数
            {
                n/=i;
                ++s;
            }
            printf("%d %d\n",i,s);
        }
    }
    if(n>1)//判断是否有大于sqrt(n)的质因子存在
        printf("%d %d\n",n,1);
    puts("");
}

三、筛质数(筛法)

/*
给定一个正整数 n，请你求出 1∼n 中质数的个数。
输入格式
共一行，包含整数 n。
输出格式
共一行，包含一个整数，表示 1∼n 中质数的个数。
数据范围
1≤n≤1e6
输入样例：
8
输出样例：
4
*/

①.朴素筛法(O(nlog n))

朴素筛法的主要思想:在遍历的过程中，将其倍数全部筛去，那么剩下的全是质数.

//朴素筛法
#include <iostream>
using namespace std;
const int N=1e6+10;
bool st[N];
int cnt,prime[N];
void get_prime(int n);

int main()
{
    int n;
    scanf("%d",&n);
    get_prime(n);
    printf("%d\n",cnt);
    return 0;
}
void get_prime(int n)
{
    for(int i=2;i<=n;++i)
    {
        if(!st[i])
        {
            prime[cnt++]=i;
        }
        for(int j=i+i;j<=n;j+=i)//将所有数得倍数删去
        {
            st[j]=true;
        }
    }
}

②.埃式筛法(优化版朴素筛法)(O(nloglog n))

埃式筛法的主要思想:将所有质数的倍数删去.

//埃式筛法
#include <iostream>
using namespace std;
const int N=1e6+10;
bool st[N];
int cnt,prime[N];
void get_prime(int n);

int main()
{
    int n;
    scanf("%d",&n);
    get_prime(n);
    printf("%d\n",cnt);
    return 0;
}
void get_prime(int n)
{
    for(int i=2;i<=n;++i)
    {
        if(!st[i])//若是质数则加入prime数组
        {
            prime[cnt++]=i;
            for(int j=i+i;j<=n;j+=i)//将所有质数的倍数筛去
            {
                st[j]=true;
            }
        }
    }
}

③.线性筛(欧拉筛法)(O(n))

线性筛的主要思想:让每个合数仅被最小质因子筛去.

//线性筛法(欧拉筛法)
#include <iostream>
using namespace std;
const int N=1e6+10;
int prime[N],cnt;
bool st[N];
void get_prime(int n);

int main()
{
    int n;
    scanf("%d",&n);
    get_prime(n);
    printf("%d\n",cnt);
    return 0;
}
void get_prime(int n)
{
    for(int i=2;i<=n;++i)
    {
        if(!st[i])
            prime[cnt++]=i;
        for(int j=0;i*prime[j]<=n;++j)
        {
            st[i*prime[j]]=true;//使得合数被最小质因子筛去
            if(i%prime[j]==0)//如果该数字已经被筛则退出循环
                break;
        }
    }
}

约数

①.试除法求约数

\[\begin{align} &求一个数(d)的约数 \\ &\because a|d, \therefore \frac{d}{a}|d.又\because 大于\sqrt{d}的约数不可能成对出现。 \\ &\therefore 仅需要枚举到\sqrt{d}，在[1,\sqrt{d}]中找约数,再判断另一个约数是否相等即可. \\ &若不相等则将两个都存入一个容器中,若相等存入一个即可. \end{align} \]

/*
给定 n 个正整数 ai，对于每个整数 ai，请你按照从小到大的顺序输出它的所有约数。
输入格式
第一行包含整数 n。
接下来 n 行，每行包含一个整数 ai。
输出格式
输出共 n 行，其中第 i 行输出第 i 个整数 ai 的所有约数。
数据范围
1≤n≤100,
2≤ai≤2×109
输入样例：
2
6
8
输出样例：
1 2 3 6 
1 2 4 8 
*/
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
vector<int> getdivisors(int n);

int main()
{
    int n;
    cin>>n;
    while(n--)
    {
        int x;
        cin>>x;
        auto res=getdivisors(x);
        for(auto t:res)
        {
            cout<<t<<' ';
        }
        puts("");
    }
    return 0;
}
vector<int> getdivisors(int n)
{
    vector<int> res;
    for(int i=1;i<=n/i;++i)
    {
        if(n%i==0)
        {
            res.push_back(i);
            if(i!=n/i)//若另一半约数相同,则只需存放一个
                res.push_back(n/i);
        }
    }
    sort(res.begin(),res.end());//将所有约数排序
    return res;
}

②.约数个数

对于一个大于1正整数n可以分解质因数：（分解质因数方法参考前文）

则n的正约数的个数就是

\[\begin{align} &上述公式基于算术基本定理以及乘法定理. \\ &算术基本定理:每一个大于1的自然数，若其本身不是质数，则可被写为两个质数以上的乘积. \\ &并且在不考虑排列顺序的情况下，正整数分解质因子的乘积是唯一的. \\ &显然p_1^{a_1}它的因子有a_1+1个. \\ &以此类推总的个数公式即可得出. \end{align} \]

/*
给定 n 个正整数 ai，请你输出这些数的乘积的约数个数，答案对 109+7 取模。
输入格式
第一行包含整数 n。
接下来 n 行，每行包含一个整数 ai。
输出格式
输出一个整数，表示所给正整数的乘积的约数个数，答案需对 109+7 取模。
数据范围
1≤n≤100,
1≤ai≤2×109
输入样例：
3
2
6
8
输出样例：
12
*/
#include <iostream>
#include <algorithm>
#include <unordered_map>
using namespace std;
typedef long long LL;
const LL mod=1e9+7;

int main()
{
    int n;
    cin>>n;
    unordered_map<int,int> primes;
    while(n--)
    {
        int x;
        cin>>x;
        for(int i=2;i<=x/i;++i)
        {
            while(x%i==0)
            {
                primes[i]++;
                x/=i;
            }
        }
        if(x>1)//所有质因子分解完判断是否存在剩余的最后一个>sqrt(x)的因子
        {
            primes[x]++;
        }
    }
    LL res=1;
    for(auto t:primes)
    {
        res=res*(t.second+1)%mod;//根据公式在计算过程中取模以防溢出
    }
    cout<<res<<endl;
    return 0;
}

③.约数之和

\[f(n)=(p_1^0+p_1^1+p_1^2+…p_1^{a_1})(p_2^0+p_2^1+p_2^2+…p_2^{a_2})…(p_k^0+p_k^1+p_k^2+…pk^{a_k}) \]

\[\begin{align} &将上述公式展开即可发现展开式中包含所有约数.\\ &在计算过程中可使用秦九韶算法简化.\\ &秦九韶算法请参考前文 \end{align} \]

/*
给定 n 个正整数 ai，请你输出这些数的乘积的约数之和，答案对 109+7 取模。
输入格式
第一行包含整数 n。
接下来 n 行，每行包含一个整数 ai。
输出格式
输出一个整数，表示所给正整数的乘积的约数之和，答案需对 109+7 取模。
数据范围
1≤n≤100,
1≤ai≤2×109
输入样例：
3
2
6
8
输出样例：
252
*/
#include <iostream>
#include <algorithm>
#include <unordered_map>
using namespace std;
typedef long long LL;
const LL mod=1e9+7;

int main()
{
    int n;
    cin>>n;
    unordered_map<int,int> primes;
    while(n--)//质因子分解并存储
    {
        int x;
        cin>>x;
        for(int i=2;i<=x/i;++i)
        {
            while(x%i==0)
            {
                primes[i]++;
                x/=i;
            }
        }
        if(x>1)
            primes[x]++;
    }
    LL res=1;
    for(auto t:primes)
    {
        LL p=t.first;
        LL q=t.second;
        LL tmp=1;
        while(q--)
        {
            tmp=(tmp*p+1)%mod;//秦九韶算法
        }
        res=res*tmp%mod;
    }
    cout<<res<<endl;
    return 0;
}

④.最大公约数(欧几里得算法(辗转相除法))

\[\begin{align} &gcd(a,b)=gcd(b,a\%b)\\ &证明:假设 d|a,d|b;且d=gcd(a,b).\\ &\because d|a,d|b \quad\therefore d|(a+b).\\ &又\because a\%b=a-(a/b)*b 注:此处a/b为整除.\\ &显然d|(a-(a/b)*b)，由此可得上式成立. \end{align} \]

/*
给定 n 对正整数 ai,bi，请你求出每对数的最大公约数。
输入格式
第一行包含整数 n。
接下来 n 行，每行包含一个整数对 ai,bi。
输出格式
输出共 n 行，每行输出一个整数对的最大公约数。
数据范围
1≤n≤105,
1≤ai,bi≤2×109
输入样例：
2
3 6
4 6
输出样例：
3
2
*/
#include <iostream>
#include <algorithm>
using namespace std;
int gcd(int a,int b);

int main()
{
    int n;
    cin>>n;
    while(n--)
    {
        int a,b;
        cin>>a>>b;
        cout<<gcd(a,b)<<endl;
        //cout<<__gcd(a,b)<<endl;//这里是两个下划线
    }
    return 0;
}
int gcd(int a,int b)
{
    return b?gcd(b,a%b):a;
    /*
    if(a<b)
        swap(a,b);
    int t;
    while(a%b)
    {
        t=a%b;
        a=b;
        b=t;
    }
    return b;
    */
}

欧拉函数

对于一个大于1正整数n可以分解质因数：（分解质因数方法参考前文）

\[\begin{align} &欧拉函数是积性函数，对于正整数n的一个算术函数 f(n)，若f(1)=1，且当a,b互质时f(ab)=f(a)f(b)，\\ &在数论上就称它为积性函数。若对于某积性函数 f(n) ，就算a, b不互质，也有f(ab)=f(a)f(b)，则称它为完全积性的\\ &两元素互斥，意为gcd(a,b)=1.\\ &欧拉函数用于计算1\thicksim N中与N互质的元素个数\\ &欧拉函数公式为:\quad \varphi(n)=n(1-\frac{1}{p_1})(1-\frac{1}{p_2})\cdots \cdots(1-\frac{1}{p_k})\\ &欧拉函数证明:基于容斥原理，我们需要寻找区间[1,N]中与N互斥的元素.当N=1时,互斥元素个数也为1.\\ &当N为质数时，显然与N互斥元素个数为N-1。当N不为质数时，我们需要删去质因子的倍数，p_1在区间\\ &中的倍数个数为\frac{N}{p_1}个，p_2的倍数在区间中个数为\frac{N}{p_2}个，后续的以此类推，之后我们需要从N个元素中减去\\ &这些质因子的倍数，但是在减去这些质因子倍数的同时可能会发生两个质因子的倍数是同一个数，因此多\\ &减去一次，所以我们需要将多减去的次数加上,但同时也会发生多加的情况，将所有情况考虑在内后，可得\\ &到一个公式为:N-\frac{N}{p_1}-\frac{N}{p_2}-\cdots \cdots+\frac{N}{p_1p_2}+\frac{N}{p_1p_3}+\cdots \cdots- \frac{N}{p_1p_2p_3}-\frac{N}{p_1p_2p_4}-\cdots \cdots,后续以此\\ &类推，将该式化简可发现与欧拉函数相等.由此得证. \end{align} \]

/*
给定 n 个正整数 ai，请你求出每个数的欧拉函数。
欧拉函数的定义参照上文.
输入格式
第一行包含整数 n。
接下来 n 行，每行包含一个正整数 ai。
输出格式
输出共 n 行，每行输出一个正整数 ai 的欧拉函数。
数据范围
1≤n≤100,
1≤ai≤2×109
输入样例：
3
3
6
8
输出样例：
2
2
4
*/
#include <iostream>
#include <algorithm>
using namespace std;
int euler(int x);

int main()
{
    int n;
    cin>>n;
    while(n--)
    {
        int x;
        cin>>x;
        cout<<euler(x)<<endl;
    }
    return 0;
}
int euler(int x)
{
    int res=x;//保证答案初始乘上x
    for(int i=2;i<=x/i;++i)//质因子分解的同时计算欧拉函数
    {
        if(x%i==0)
        {
            res=res/i*(i-1);//防止(1-1/i)发生整除
            while(x%i==0)
            {
                x/=i;
            }
        }
    }
    if(x>1)
    {
        res=res/x*(x-1);
    }
    return res;
}

\[\begin{align} &欧拉函数除了可以通过公式得到之外仍然可以通过线性筛(欧拉筛法)得到.假设欧拉函数值存放在数组phi[N]中.\\ &证明:在上文欧拉函数的基础上，证明该结论，当一个数字p为质数，显然其欧拉函数的值为\varphi(p)=p-1.\\ &若数字p不为质数，当p==1，显然\varphi(1)=1，当p!=1，且不为质数时，if(p\%primes[j]==0)，此时phi[primes[j]*p]\\ &=phi[p]*primes[j],\quad\because 此时primes[j]是p的质因子，所以primes[j]恰好是p质因子分解中的一个因，仅对该因子的\\ &次数做改变，不影响欧拉函数的值,但在最前面需要乘上primes[j]，便可以得到phi[peimes[j]*p]的值，if(p\%primes[j])\\ &即primes[j]不是p的质因子时，primes[j]是primes[j]*p的最小质因子,\varphi(prmies[j])=primes[j]*(1-\frac{1}{primes[j]})=\\ &primes[j]-1，\varphi(primes[j]*p)=phi[p]*(primes[j]-1).由此便得出如何在线性筛中求出欧拉函数的值. \end{align} \]

/*
给定一个正整数 n，求 1∼n 中每个数的欧拉函数之和。
输入格式
共一行，包含一个整数 n。
输出格式
共一行，包含一个整数，表示 1∼n 中每个数的欧拉函数之和。
数据范围
1≤n≤106
输入样例：
6
输出样例：
12
*/
#include <iostream>
#include <algorithm>
using namespace std;
const int N=1e6+10;
typedef long long LL;
int primes[N],idx,phi[N];
bool st[N];
void get_euler(int n);

int main()
{
    int n;
    cin>>n;
    get_euler(n);
    LL res=0;
    for(int i=1;i<=n;++i)
    {
        res+=phi[i];
    }
    cout<<res<<endl;
    return 0;
}

void get_euler(int n)
{
    phi[1]=1;
    for(int i=2;i<=n;++i)
    {
        if(!st[i])
        {
            primes[idx++]=i;
            phi[i]=i-1;
        }
        for(int j=0;primes[j]<=n/i;++j)
        {
            st[primes[j]*i]=true;
            if(i%primes[j]==0)
            {
                phi[primes[j]*i]=primes[j]*phi[i];
                break;
            }
            phi[primes[j]*i]=phi[i]*(primes[j]-1);
        }
    }
}

快速幂

\[\begin{align} &快速幂的作用是在O(log k)的时间复杂度下，求出\quad a^k\ mod\ p.\quad a^k我们可以看成是由a^{2^{x_1}}*a^{2^{x_2}}*\cdots\cdots *a^{2^{x_i}}.\\ &注意观察此时a的次方都是由2的x次方构成，那么我们可以将k转换成二进制数，位数为1的位置我们将对应的a\\ &x次方累乘在答案上.那么我们就需要事现处理出a^{2^{0}}，a^{2^{1}}，a^{2^{2}}\cdots\cdots，a^{2^{log k}}这些值，此处我们可以观察前后项\\ &不难发现后一项是前一项的平方，由此我们仅需要在执行的同时每步判断k的二进制位是否为1，并且对a的x次\\ &进行平方，若k的二进制位为1，则累成至答案上即可. \end{align} \]

/*
给定 n 组 ai,bi,pi，对于每组数据，求出 ai^bi mod pi 的值。
输入格式
第一行包含整数 n。
接下来 n 行，每行包含三个整数 ai,bi,pi。
输出格式
对于每组数据，输出一个结果，表示 ai^bi mod pi 的值。
每个结果占一行。
数据范围
1≤n≤100000,
1≤ai,bi,pi≤2×109
输入样例：
2
3 2 5
4 3 9
输出样例：
4
1
*/
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
LL qmi(int a,int b,int p);

int main()
{
    int n;
    scanf("%d",&n);
    while(n--)
    {
        int a,b,p;
        scanf("%d%d%d",&a,&b,&p);
        printf("%d\n",qmi(a,b,p));
    }
    return 0;
}
LL qmi(int a,int b,int p)
{
    LL res=1;
    while(b)
    {
        if(b&1)
        {
            res=res*a%p;
        }
        a=a*(LL)a%p;
        b>>=1;
    }
    return res;
}

\[\begin{align} &同时快速幂可用于求解逆元，逆元的定义如下:\\ &若整数 b，m 互质，并且对于任意的整数 a，如果满足 b|a，则存在一个整数 x，使得 a/b≡a×x(mod\ m)，\\ &则称 x 为 b 的模 m 乘法逆元，记为 b^{-1}(mod\ m).b 存在乘法逆元的充要条件是 b 与模数 m 互质.\\ &当模数 m 为质数时，b^{m-2}即为 b 的乘法逆元.\\ &若对于正整数a和m，存在a*x≡1(mod\ m)，则把这个同余方程中x最小正整数的解称作a模m的逆元.\\ &若m为质数，更具费马小定理可以得到逆元为a^{m-2}mod\ m.\\ &注:当a是p的倍数时，逆元不存在. \end{align} \]

/*
给定 n 组 ai,pi，其中 pi 是质数，求 ai 模 pi 的乘法逆元，若逆元不存在则输出 impossible。
注意：请返回在 0∼p−1 之间的逆元。
输入格式
第一行包含整数 n。
接下来 n 行，每行包含一个数组 ai,pi，数据保证 pi 是质数。
输出格式
输出共 n 行，每组数据输出一个结果，每个结果占一行。
若 ai 模 pi 的乘法逆元存在，则输出一个整数，表示逆元，否则输出 impossible。
数据范围
1≤n≤105,
1≤ai,pi≤2∗109
输入样例：
3
4 3
8 5
6 3
输出样例：
1
2
impossible
*/
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
LL qmi(int a,int b,int p);

int main()
{
    int n;
    cin>>n;
    while(n--)
    {
        int a,p;
        cin>>a>>p;
        if(a%p==0)
            puts("impossible");
        else
            cout<<qmi(a,p-2,p)<<endl;
    }
    return 0;
}
LL qmi(int a,int b,int p)
{
    LL res=1;
    while(b)
    {
        if(b&1)
            res=res*a%p;
        a=a*(LL)a%p;
        b>>=1;
    }
    return res;
}

拓展欧几里得算法

\[\begin{align} &裴属定理:对于任何正整数a，b以及他们的最大公约数d，关于未知数x，y的线性不定方程称为裴属等式.\\ &即:a，b为整数，且gcd(a,b)=d,那么对于任意的整数x，y，ax+by=kgcd(a,b)，k表示整数倍.特别的\\ &一定存在x，y使得ax+by=gcd(a,b)，若a，b互质，则ax+by=1.\\ &而拓展欧几里得算法就是在求解出gcd(a,b)的同时可以满足裴属定理的ax+by=gcd(a,b)的等式，求解出\\ &满足条件的x，y. \end{align} \]

/*
给定 n 对正整数 ai,bi，对于每对数，求出一组 xi,yi，使其满足 ai*xi+bi*yi=gcd(ai,bi)。
输入格式
第一行包含整数 n。
接下来 n 行，每行包含两个整数 ai,bi。
输出格式
输出共 n 行，对于每组 ai,bi，求出一组满足条件的 xi,yi，每组结果占一行。
本题答案不唯一，输出任意满足条件的 xi,yi 均可。
数据范围
1≤n≤105,
1≤ai,bi≤2×109
输入样例：
2
4 6
8 18
输出样例：
-1 1
-2 1
*/
#include <iostream>
using namespace std;
int exgcd(int a,int b,int &x,int &y);

int main()
{
    int n;
    scanf("%d",&n);
    while(n--)
    {
        int a,b,x,y;
        scanf("%d%d",&a,&b);
        exgcd(a,b,x,y);
        printf("%d %d\n",x,y);
    }
    return 0;
}
int exgcd(int a,int b,int &x,int &y)
{
    if(b==0)
    {
        x=1,y=0;//b的系数为0,a的系数为1.
        return a;
    }
    else
    {
        int d=exgcd(b,a%b,y,x);//传入(b,a%b,y,x)方便推到计算
        y-=a/b*x;
        return d;
    }
}

\[\begin{align} &同时我们可以利用拓展欧几里得去求解线性同余方程\\ &例:线性同余方程 \quad a*x\equiv\ b(mod\ m).\\ &将方程转换一个形式得: \ a*x-\frac{a*x}{m}*m=b，之后可写成\ a*x=y'*m+b，\\ &移项得 a*x-y'*m=b，另y=-y'，得\ a*x+m*y=b，至此我们可以发现\\ &我们可以利用拓展欧几里得求解.但是拓展欧几里得需要满足条件才会有解，即条\\ &件为:\ gcd(a,m)|b，即b为gcd(a,m)的倍数，若不满足该条件则无解. \end{align} \]

/*
给定 n 组数据 ai,bi,mi，对于每组数求出一个 xi，使其满足 ai*xi≡bi(mod mi)，如果无解则输出 impossible。
输入格式
第一行包含整数 n。
接下来 n 行，每行包含一组数据 ai,bi,mi。
输出格式
输出共 n 行，每组数据输出一个整数表示一个满足条件的 xi，如果无解则输出 impossible。
每组数据结果占一行，结果可能不唯一，输出任意一个满足条件的结果均可。
输出答案必须在 int 范围之内。
数据范围
1≤n≤105,
1≤ai,bi,mi≤2×109
输入样例：
2
2 3 6
4 3 5
输出样例：
impossible
-3
*/
#include <iostream>
using namespace std;
typedef long long LL;
int exgcd(int a,int b,int &x,int &y);

int main()
{
    int n;
    scanf("%d",&n);
    while(n--)
    {
        int a,b,m;
        int x,y;
        scanf("%d%d%d",&a,&b,&m);
        int d=exgcd(a,m,x,y);
        if(b%d)
            puts("impossible");
        else
            printf("%d\n",(LL)x*b/d %m);//扩大b/d倍并且模到0-m的范围内
    }
    return 0;
}
int exgcd(int a,int b,int &x,int &y)
{
    if(b==0)
    {
        x=1,y=0;
        return a;
    }
    else
    {
        int d=exgcd(b,a%b,y,x);
        y-=a/b*x;
        return d;
    }
}

中国剩余定理

\[\begin{align} &中国剩余定理:另m_1,m_2,m_3,\cdots\cdots,m_n为大于1的两两互质的正整数，而a_1,a_2,a_3,\cdots\cdots,a_n为任意正整数.\\ &则同余方程组为:\\ \end{align} \]

\[\begin{align} \begin{cases} x\equiv\ a_1(mod\ m_1),\\ x\equiv\ a_2(mod\ m_2),\\ x\equiv\ a_3(mod\ m_3),\\ \quad \quad .\\ \quad \quad .\\ \quad \quad .\\ x\equiv\ a_n(mod\ m_n)\\ \end{cases} \end{align} \]

\[\begin{align} &另M=m_1*m_2*m_3*\cdots\cdots*m_n\ .\quad 另M_i=\frac{M}{m_i}(0\leq i \leq n)，\\ &由此可以看出M_i与m_i互质，即gcd(M_i,m_i)=1，而此时便存在\\ &整数y_i为M_i模m_i的逆，使得M_i*y_i\ \equiv\ 1(mod\ m_i).\\ &此时可以得到同余方程组的解为: x=a_1*M_1*y_1+a_2*M_2*y_2+\cdots\cdots+a_n*M_n*y_n. \end{align} \]

\[\begin{align} &而将中国剩余定理利用到下题求解时，需做推导，因为下题中并没有保证m_1,m_2,\cdots\cdots,m_n两两互质.\\ & \end{align} \]

/*
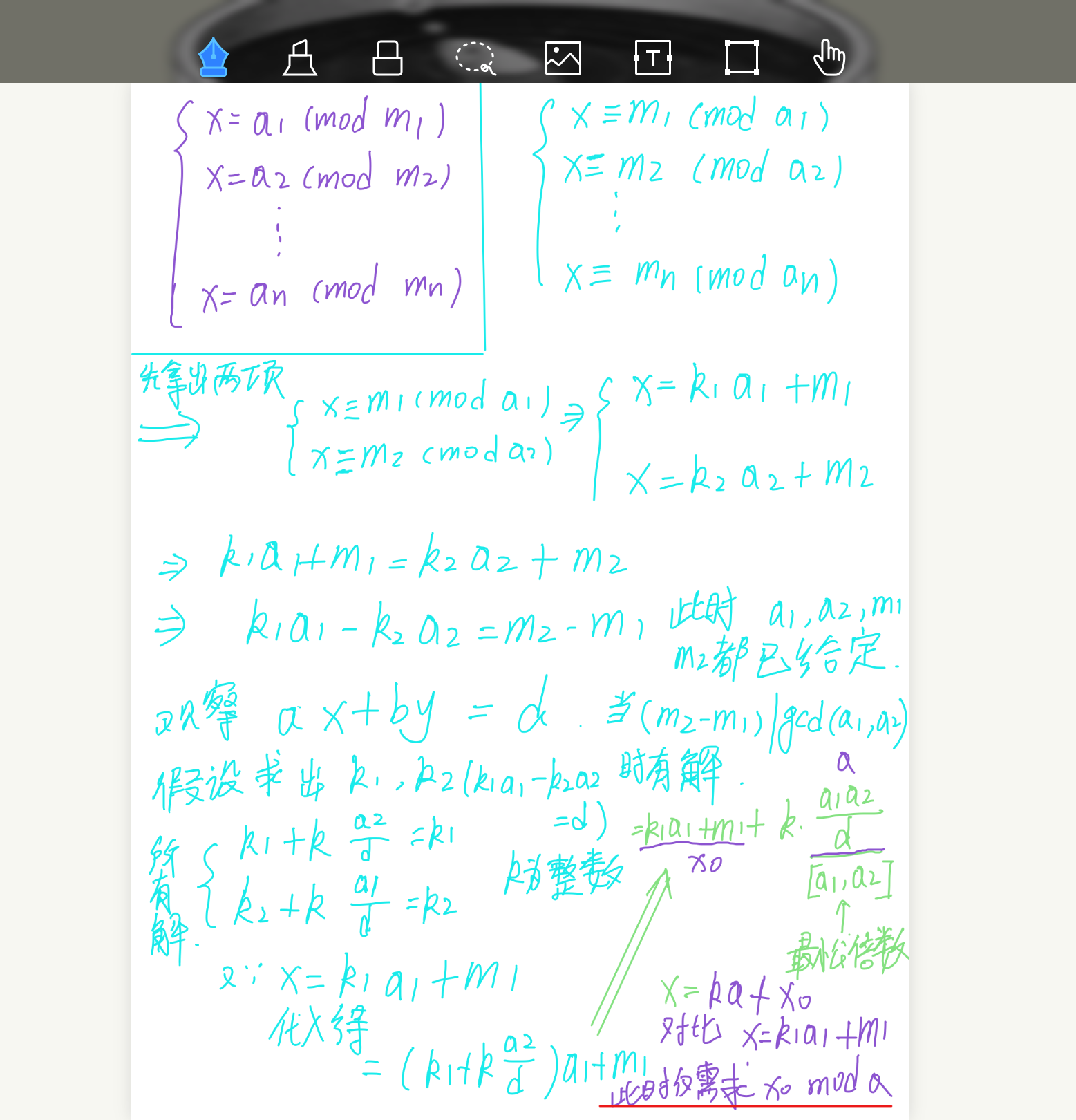
给定 2n 个整数 a1,a2,…,an 和 m1,m2,…,mn，求一个最小的非负整数 x，满足 ∀i∈[1,n],x≡mi(mod ai)。
输入格式
第 1 行包含整数 n。
第 2…n+1 行：每 i+1 行包含两个整数 ai 和 mi，数之间用空格隔开。
输出格式
输出最小非负整数 x，如果 x 不存在，则输出 −1。
如果存在 x，则数据保证 x 一定在 64 位整数范围内。
数据范围
1≤ai≤231−1,
0≤mi<ai
1≤n≤25
输入样例：
2
8 7
11 9
输出样例：
31
*/
#include <iostream>
#include <cmath>
using namespace std;
typedef long long LL;
LL exgcd(LL a,LL b,LL &x,LL &y);

int main()
{
    int n;
    cin>>n;
    LL a1,m1;
    cin>>a1>>m1;
    bool flag=true;
    for(int i=0;i<n-1;++i)
    {
        LL a2,m2;
        cin>>a2>>m2;
        LL k1,k2;
        LL d=exgcd(a1,a2,k1,k2);
        if((m2-m1)%d)
        {
            flag=false;
            break;
        }
        k1*=((m2-m1)/d);
        LL t=a2/d;
        k1=(k1%t+t)%t;
        m1=a1*k1+m1;
        a1=abs(a1/d*a2);
        //a1=abs(a1*a2/d);
        
    }
    if(flag)
        cout<<(m1%a1+a1)%a1<<endl;
    else
        puts("-1");
    return 0;
}

LL exgcd(LL a,LL b,LL &x,LL &y)
{
    if(b==0)
    {
        x=1,y=0;
        return a;
    }
    else
    {
        LL d=exgcd(b,a%b,y,x);
        y-=a/b*x;
        return d;
    }
}

高斯消元

\[\begin{align} &高斯消元是用于求解线性方程组的一种方法，现有如下线性方程组: \end{align} \]

\[\begin{align} \begin{cases} a_{11}x_1+a_{12}x_2+\cdots\cdots+a_{1n}x_n=b_1,\\ a_{21}x_1+a_{22}x_2+\cdots\cdots+a_{2n}x_n=b_2,\\ a_{31}x_1+a_{32}x_2+\cdots\cdots+a_{3n}x_n=b_3,\\ \quad\quad\quad\quad\quad.\\ \quad\quad\quad\quad\quad.\\ \quad\quad\quad\quad\quad.\\ a_{n1}x_1+a_{n2}x2+\cdots\cdots+a_{nn}x_n=b_n \end{cases} \end{align} \]

\[\begin{align} &初等变化包含如下:\\ &①.方程组中任意两行方程交换位置\\ &②.用非零的任意数字乘任意一行方程\\ &③.将某一方程的倍数加至另一方程\\ &通过一系列操作后(即经过一系列初等变化)，我们将方程形式转换成阶梯型(上三角)线性方程组.\\ &若该方程组中出现某一方程左边=0，而右边非0，则该方程组无解.\\ &若该方程组出现方程总数量减少，那么该方程有无数组解.\\ &若方程组恰好最后成阶梯型方程组且方程数量未变，则有唯一的解.\\ &对方程组进行如下操作可得到阶梯型方程，再判断是否有解.\\ &依次枚举每一列行，当处理第一列的时候，找出第一列的绝对值最大的系数，将此方程与当前第一行方程交换位置.\\ &交换完位置后，将该方程整体除以第一个系数，使得该方程第一个变量的系数为1.之后通过初等变化中③的操作\\ &将除第一行外的所有方程的第一个系数去除，至此遍历第一列结束，然后从第二行第二列开始进行相同的操作，\\ &直至处理完所有方程，那么最后也会将方程组转换成阶梯型方程组，之后再进一步判断.如需进一步得到方程的解，\\ &那么我们需要从最后一行往上递推(由于处理到最后一行结束时，最后一行必定已经将方程最后的一变量求出，所以\\ &我们仅需倒着递推一遍就可以得到所有变量的结果). \end{align} \]

/*
输入一个包含 n 个方程 n 个未知数的线性方程组。
方程组中的系数为实数。
求解这个方程组。(参考上方方程组)
输入格式
第一行包含整数 n。
接下来 n 行，每行包含 n+1 个实数，表示一个方程的 n 个系数以及等号右侧的常数。
输出格式
如果给定线性方程组存在唯一解，则输出共 n 行，其中第 i 行输出第 i 个未知数的解，结果保留两位小数。
如果给定线性方程组存在无数解，则输出 Infinite group solutions。
如果给定线性方程组无解，则输出 No solution。
数据范围
1≤n≤100,
所有输入系数以及常数均保留两位小数，绝对值均不超过 100。
输入样例：
3
1.00 2.00 -1.00 -6.00
2.00 1.00 -3.00 -9.00
-1.00 -1.00 2.00 7.00
输出样例：
1.00
-2.00
3.00
*/
#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;
const double eps=1e-6;
const int N=110;
double a[N][N];
int n;
int gauss();

int main()
{
    cin>>n;
    for(int i=0;i<n;++i)
        for(int j=0;j<n+1;++j)
            cin>>a[i][j];
    int t=gauss();
    if(t==0)//返回0代表有唯一的解
    {
        for(int i=0;i<n;++i)
        {
            printf("%.2lf\n",a[i][n]);
        }
    }
    else if(t==1)
        puts("Infinite group solutions");
    else
        puts("No solution");
    return 0;
}

int gauss()
{
    int c,r;
    for(c=0,r=0;c<n;++c)
    {
        int t=r;
        for(int i=r;i<n;++i)
        {
            if(fabs(a[i][c])>fabs(a[r][c]))
                t=i;
        }
        if(fabs(a[t][c])<eps) 
            continue;
        
        for(int i=0;i<n+1;++i)
            swap(a[r][i],a[t][i]);
        
        for(int i=n;i>=0;--i)
            a[r][i]/=a[r][c];
        
        for(int i=r+1;i<n;++i)
        {
            if(fabs(a[i][c])>eps)
            {
                for(int j=n;j>=c;--j)
                {
                    a[i][j]-=(a[r][j]*a[i][c]);
                }
            }
        }
        ++r;
    }
    if(r<n)
    {
        for(int i=r;i<n;++i)
        {
            if(fabs(a[i][n])>eps)
                return 2;
        }
        return 1;
    }
    
    for(int i=n-1;i>=0;--i)
    {
        for(int j=i+1;j<n;++j)
        {
            a[i][n]-=(a[j][n]*a[i][j]);
        }
    }
    
    return 0;
}

/*
输入一个包含 n 个方程 n 个未知数的异或线性方程组。
方程组中的系数和常数为 0 或 1，每个未知数的取值也为 0 或 1。
求解这个方程组。
异或线性方程组示例如下：
M[1][1]x[1] ^ M[1][2]x[2] ^ … ^ M[1][n]x[n] = B[1]
M[2][1]x[1] ^ M[2][2]x[2] ^ … ^ M[2][n]x[n] = B[2]
…
M[n][1]x[1] ^ M[n][2]x[2] ^ … ^ M[n][n]x[n] = B[n]
其中 ^ 表示异或(XOR)，M[i][j] 表示第 i 个式子中 x[j] 的系数，B[i] 是第 i 个方程右端的常数，取值均为 0 或 1。
输入格式
第一行包含整数 n。
接下来 n 行，每行包含 n+1 个整数 0 或 1，表示一个方程的 n 个系数以及等号右侧的常数。
输出格式
如果给定线性方程组存在唯一解，则输出共 n 行，其中第 i 行输出第 i 个未知数的解。
如果给定线性方程组存在多组解，则输出 Multiple sets of solutions。
如果给定线性方程组无解，则输出 No solution。
数据范围
1≤n≤100
输入样例：
3
1 1 0 1
0 1 1 0
1 0 0 1
输出样例：
1
0
0
*/
#include <iostream>
#include <algorithm>
using namespace std;
const int N=110;
int a[N][N];
int n;
int gauss();

int main()
{
    cin>>n;
    for(int i=0;i<n;++i)
    {
        for(int j=0;j<n+1;++j)
        {
            cin>>a[i][j];
        }
    }
    
    int t=gauss();
    if(!t)
    {
        for(int i=0;i<n;++i)
            cout<<a[i][n]<<endl;
    }
    else if(t==1)
        puts("Multiple sets of solutions");
    else
        puts("No solution");
    
    return 0;
}

int gauss()
{
    int r,c;
    for(c=0,r=0;c<n;++c)
    {
        int t=r;
        for(int i=r;i<n;++i)
        {
            if(a[i][c])
            {
                t=i;
                break;
            }
        }
        if(!a[t][c])
            continue;
        for(int i=c;i<n+1;++i)
        {
            swap(a[t][i],a[r][i]);
        }
        for(int i=r+1;i<n;++i)
        {
            if(a[i][c])
            {
                for(int j=c;j<n+1;++j)
                {
                    a[i][j]^=a[r][j];
                }
            }
        }
        ++r;
    }
    if(r<n)
    {
        for(int i=r;i<n;++i)
        {
            if(a[i][n])
                return 2;
        }
        return 1;
    }
    
    for(int i=n-1;i>=0;--i)
    {
        for(int j=i+1;j<n;++j)
        {
            a[i][n]^=(a[i][j]&a[j][n]);
        }
    }
    return 0;
}

组合数

\[\begin{align} &帕斯卡恒等式：C_{a}^b=C_{a-1}^b+C_{a-1}^{b-1}\\ &C_{a}^b=\frac{a!}{b!(a-b)!}\\ &卢卡斯定理(lucas)：\quad C_{a}^b=C_{a\ mod\ p}^{b\ mod\ p}*C_{a/p}^{b/p}(mod\ p)\ 时间复杂度(O(Nlog_pN))\\ &针对于不同的数据范围我们选择不同的方法去计算组合数.\\ &卢卡斯定理证明如下: \end{align} \]

\[\begin{align} &当我们需要将组合数最后的结果求出并且该结果非常大的时候我们就需要利用高精度.\\ &C_{a}^b=\frac{a!}{b!(a-b)!}\\ &此时利用该公式可计算，但是倘若直接对阶乘进行高精度乘法将会十分繁琐，所以我们对\\ &其直接质因子分解，在分解时可以通过分子的某质因子直接将分母的质因子抵消，到最后\\ &仅需要实现高精度乘法即可.但与此同时我们需要解决阶乘的质因子分解这一问题，当考\\ &虑质因子p时，N！中p的个数应该为\frac{N}{p}+\frac{N}{p^2}+\frac{N}{p^3}+\cdots\cdots，直到p^x>N(此处全为下取整)\\ &\frac{N}{p}表示的是[1,N]中p的倍数的个数，之后的算式含义也是如此.因为当计算完所有p的倍数个数，\\ &p^2中将会有一个没有加入，p^3中将会有两个没有加入，因此需要将所有的加入，如此才得到等式.\\ &至此便可得到N!中质因子p的次数.此时通过公式便可化简成一个仅有乘法的式子. \end{align} \]

/*
给定 n 组询问，每组询问给定两个整数 a，b，请你输出 C(a,b)mod(109+7) 的值。
输入格式
第一行包含整数 n。
接下来 n 行，每行包含一组 a 和 b。
输出格式
共 n 行，每行输出一个询问的解。
数据范围
1≤n≤10000,
1≤b≤a≤2000
输入样例：
3
3 1
5 3
2 2
输出样例：
3
10
1
*/
#include <iostream>
#include <algorithm>
using namespace std;
const int N=2e3+10,mod=1e9+7;
int c[N][N];
void init();

int main()
{
    init();
    int n;
    scanf("%d",&n);
    while(n--)
    {
        int a,b;
        scanf("%d%d",&a,&b);
        printf("%d\n",c[a][b]);
    }
    return 0;
}

void init()
{
    for(int i=0;i<N;++i)
    {
        for(int j=0;j<=i;++j)
        {
            if(!j)
                c[i][j]=1;
            else
                c[i][j]=(c[i-1][j]+c[i-1][j-1])%mod;
        }
    }
}

/*
给定 n 组询问，每组询问给定两个整数 a，b，请你输出 C(a,b)mod(109+7) 的值。
输入格式
第一行包含整数 n。
接下来 n 行，每行包含一组 a 和 b。
输出格式
共 n 行，每行输出一个询问的解。
数据范围
1≤n≤10000,
1≤b≤a≤105
输入样例：
3
3 1
5 3
2 2
输出样例：
3
10
1
*/
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N=1e5+10,mod=1e9+7;
int fact[N],infact[N];
int qmi(int a,int k,int p);
void init();

int main()
{
    init();
    int n;
    scanf("%d",&n);
    while(n--)
    {
        int a,b;
        scanf("%d%d",&a,&b);
        printf("%d\n",(LL)fact[a]*infact[b]%mod*infact[a-b]%mod);
    }
    return 0;
}

int qmi(int a,int k,int p)
{
    LL res=1;
    while(k)
    {
        if(k&1)
            res=(LL)res*a%p;
        a=(LL)a*a%p;
        k>>=1;
    }
    return res;
}

void init()
{
    fact[0]=infact[0]=1;
    for(int i=1;i<N;++i)
    {
        fact[i]=(LL)fact[i-1]*i%mod;
        infact[i]=(LL)infact[i-1]*qmi(i,mod-2,mod)%mod;
    }
}

/*
给定 n 组询问，每组询问给定三个整数 a,b,p，其中 p 是质数，请你输出 C(a,b)modp 的值。
输入格式
第一行包含整数 n。
接下来 n 行，每行包含一组 a,b,p。
输出格式
共 n 行，每行输出一个询问的解。
数据范围
1≤n≤20,
1≤b≤a≤1018,
1≤p≤105,
输入样例：
3
5 3 7
3 1 5
6 4 13
输出样例：
3
3
2
*/
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
int p;
int qmi(int a,int k);
LL C(int a,int b);
LL lucas(LL a,LL b);

int main()
{
    int n;
    cin>>n;
    while(n--)
    {
        LL a,b;
        cin>>a>>b>>p;
        cout<<lucas(a,b)<<endl;
    }
    return 0;
}

int qmi(int a,int k)
{
    LL res=1;
    while(k)
    {
        if(k&1)
            res=(LL)res*a%p;
        a=(LL)a*a%p;
        k>>=1;
    }
    return res;
}

LL C(int a,int b)
{
    if(b>a)
        return 0;
    LL res=1;
    for(int i=1,j=a;i<=b;++i,--j)
    {
        res=(LL)res*j%p;
        res=res*qmi(i,p-2)%p;
    }
    return res;
}

LL lucas(LL a,LL b)
{
    if(a<p&&b<p)
        return C(a,b);
    return (LL)C(a%p,b%p)*lucas(a/p,b/p)%p;
}

/*
输入 a,b，求 C(a,b) 的值。
注意结果可能很大，需要使用高精度计算。
输入格式
共一行，包含两个整数 a 和 b。
输出格式
共一行，输出 C(a,b) 的值。
数据范围
1≤b≤a≤5000
输入样例：
5 3
输出样例：
10
*/
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
const int N=5010;
int primes[N],idx,sum[N];
bool st[N];
void get_primes(int n);
int get(int n,int p);
vector<int> mul(vector<int> a,int b);

int main()
{
    int a,b;
    cin>>a>>b;
    get_primes(a);
    
    for(int i=0;i<idx;++i)
    {
        int p=primes[i];
        sum[i]=get(a,p)-get(b,p)-get(a-b,p);
    }
    
    vector<int> res;
    res.push_back(1);
    
    for(int i=0;i<idx;++i)
    {
        for(int j=0;j<sum[i];++j)
        {
            res=mul(res,primes[i]);
        }
    }
    
    for(int i=res.size()-1;i>=0;--i)
    {
        cout<<res[i];
    }
    puts("");
    
    return 0;
}

void get_primes(int n)
{
    for(int i=2;i<=n;++i)
    {
        if(!st[i])
        {
            primes[idx++]=i;
        }
        for(int j=0;primes[j]<=n/i;++j)
        {
            st[primes[j]*i]=true;
            if(i%primes[j]==0)
                break;
        }
    }
}

int get(int n,int p)
{
    int res=0;
    while(n)
    {
        res+=n/p;
        n/=p;
    }
    return res;
}

vector<int> mul(vector<int> a,int b)
{
    vector<int> c;
    int t=0;
    for(int i=0;i<a.size();++i)
    {
        t+=a[i]*b;
        c.push_back(t%10);
        t/=10;
    }
    while(t)
    {
        c.push_back(t%10);
        t/=10;
    }
    return c;
 }

\[\begin{align} &卡特兰数\\ &通项为:\ C_n=\frac{1}{n+1}C_{2n}^{n}\\ &满足递推式:\ C_1=1，C_n=C_{n-1}\frac{4n-2}{n+1}，C_{n+1}=C_{0}C_{n}+C_{1}c_{n-1}+\cdots\cdots+C_{n}C_{0}\\ \end{align} \]

/*
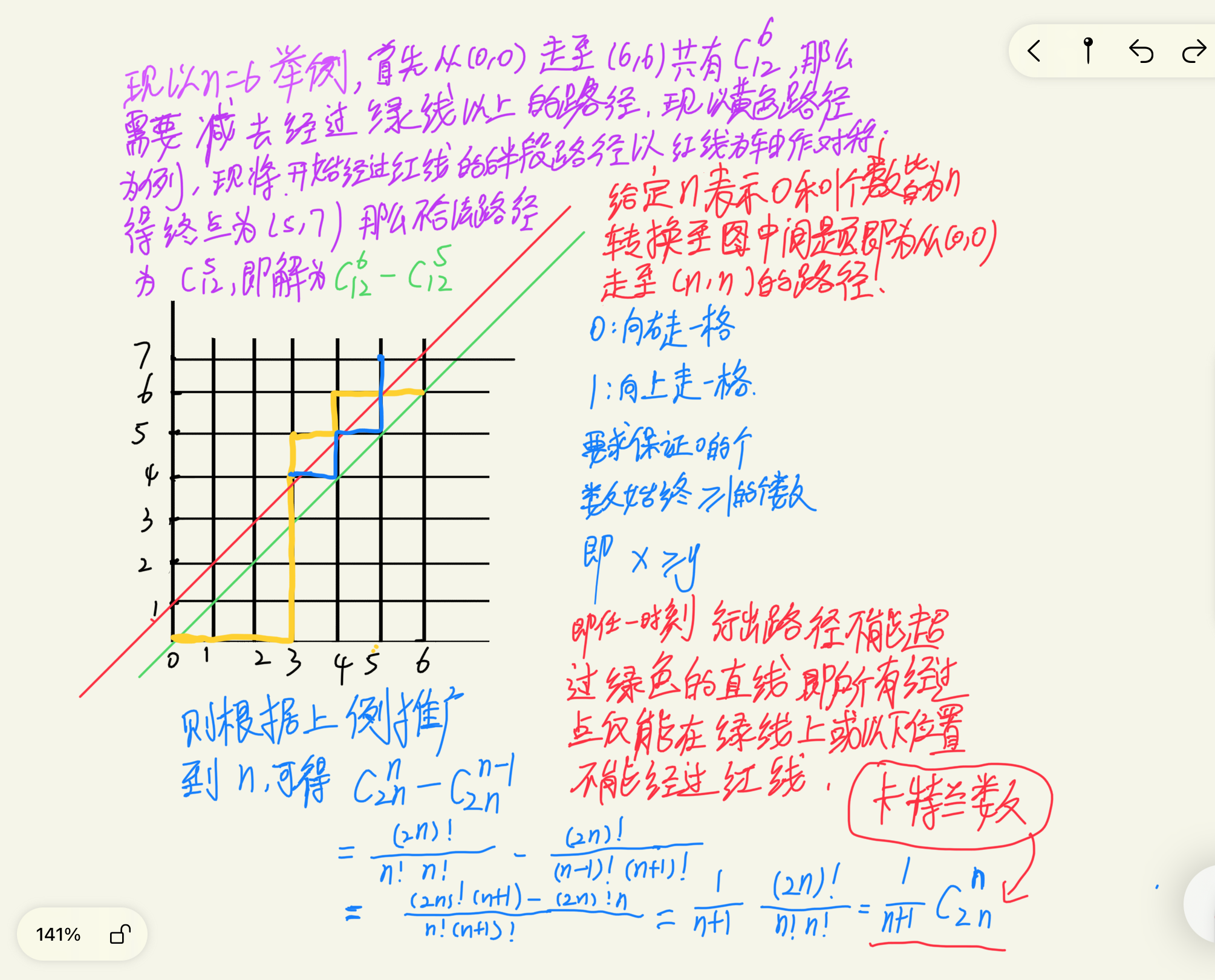
给定 n 个 0 和 n 个 1，它们将按照某种顺序排成长度为 2n 的序列，求它们能排列成的所有序列中，能够满足任意前缀序列中 0 的个数都不少于 1 的个数的序列有多少个。
输出的答案对 109+7 取模。
输入格式
共一行，包含整数 n。
输出格式
共一行，包含一个整数，表示答案。
数据范围
1≤n≤105
输入样例：
3
输出样例：
5
/*
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
const int mod=1e9+7;
int qmi(int a,int k,int p);

int main()
{
    int n;
    cin>>n;
    int a=2*n,b=n;
    LL res=1;
    for(int i=a;i>=a-b+1;--i)
    {
        res=(LL)res*i%mod;
    }
    for(int i=b;i>0;--i)
    {
        res=(LL)res*qmi(i,mod-2,mod)%mod;
    }
    res=(LL)res*qmi(n+1,mod-2,mod)%mod;
    cout<<res<<endl;
    return 0;
}

int qmi(int a,int k,int p)
{
    LL res=1;
    while(k)
    {
        if(k&1)
        {
            res=(LL)res*a%p;
        }
        a=(LL)a*a%p;
        k>>=1;
    }
    return res;
}

容斥原理

\[\begin{align} &当我们存在两个相交集合A和B时，我们需要求两个集合的元素的总和.以及当我们有三个相交集合A和B和C时，\\ &我们需要求三个集合元素的总和，见下图. \end{align} \]

\[\begin{align} &根据上述我们将其推广至n个相交集合，求集合元素总和，我们可得:\\ &|S_1∪S_2∪S_3∪\cdots\cdots∪S_n|=\sum_{0\leq i\leq n}({S_i})\ -\sum_{0\leq i< j\leq n}({S_i∩S_j})\ +\sum_{0\leq i<j<k\leq n}({S_i∩S_j∩S_k})-\cdots+(-1)^{n-1}(S_i∩S_j\cdots∩S_n)\\ &由(1+x)^n 二项式定理展开后另x=1,可得C_{n}^{0}+C_{n}^{1}+C_{n}^{2}+\cdots\cdots+C_{n}^{n}=2^n\\ &对于容斥原理的公式不妨假设x出现在k个集合中(1\leq k\leq n)，那么在左右等式中值应都为1.\\ &对于右边=C_{k}^{1}-C_{k}^{2}+C_{k}^{3}-\cdots\cdots+(-1)^{n-1}C_{k}^{k}，此时通过二项式定理(1+x)^n展开另x=-1可推出右边=1.\\ &则容斥原理得证，(另:容斥原理可用数学归纳法证明) \end{align} \]

\[\begin{align} &例题中寻找1-n中1能被m个质数整除的数的个数，1-n中p的倍数有\frac{n}{p}个，若是两个质数共同的倍数则有\frac{n}{p_1p_2}个\\ &以此类推m个质数共同倍数有\frac{n}{p_1p_2\cdots p_m}个.需要计算(能被质数)至少有一个数整除的数的个数.此处利用容斥原理\\ &求解，一个质数倍数的-两个质数倍数的+三个质数倍数的-\cdots\cdots.但针对本题，可以使用二进制压位操作k个\\ &质数，可以将k看为m位的二进制数，位数上为1的代表选择这个质数，又因为总共有2^m-1种所以最外层需要循环\\ &2^m-1次，这样可以将所有选取方式表示出来. \end{align} \]

/*
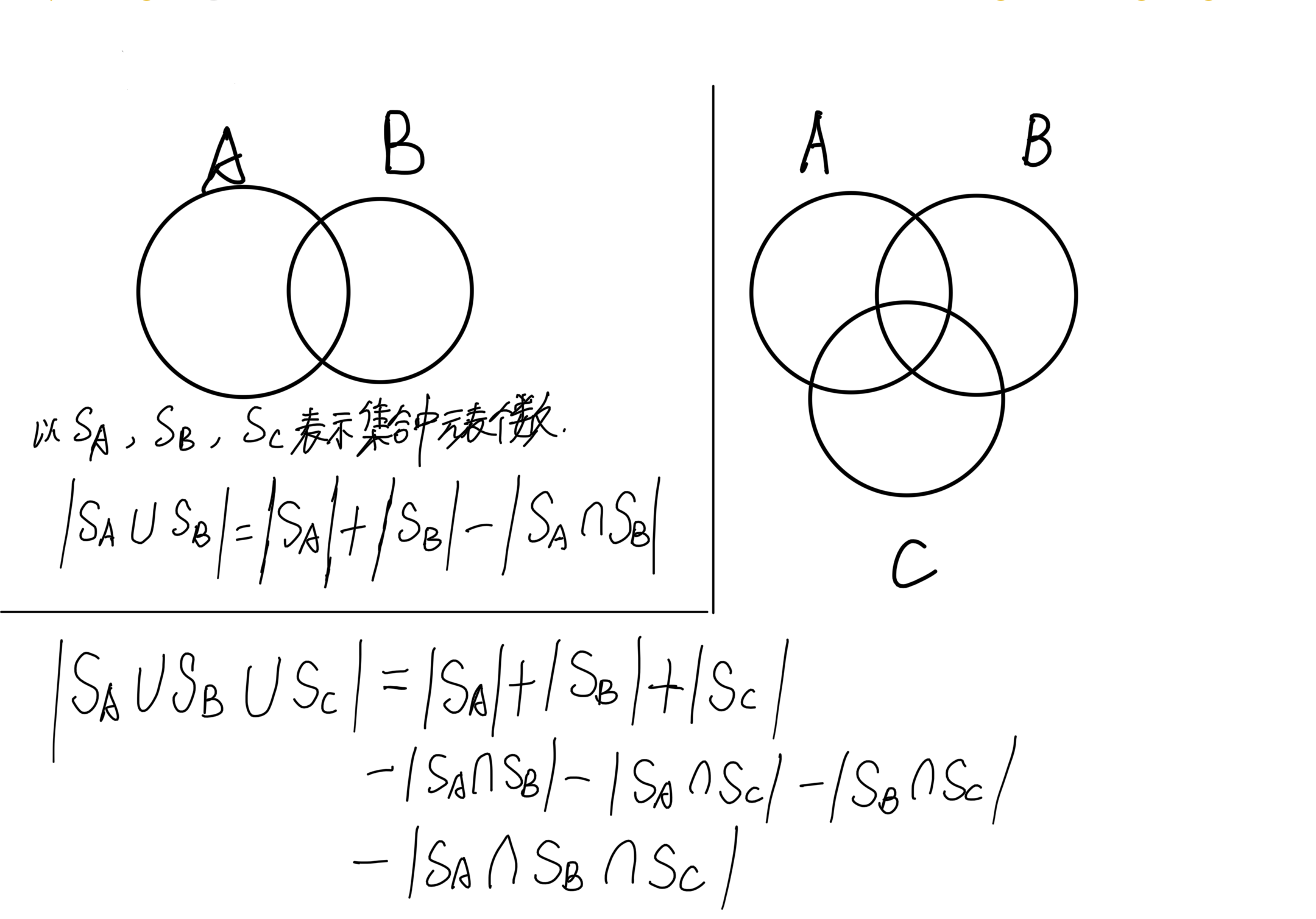
给定一个整数 n 和 m 个不同的质数 p1,p2,…,pm。
请你求出 1∼n 中能被 p1,p2,…,pm 中的至少一个数整除的整数有多少个。
输入格式h
第一行包含整数 n 和 m。
第二行包含 m 个质数。
输出格式
输出一个整数，表示满足条件的整数的个数。
数据范围
1≤m≤16,
1≤n,pi≤109
输入样例：
10 2
2 3
输出样例：
7
*/
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N=20;
int p[N],n,m;

int main()
{
    cin>>n>>m;
    for(int i=0;i<m;++i)
    {
        cin>>p[i];
    }
    int res=0;
    for(int i=1;i<1<<m;++i)
    {
        int t=1,cnt=0;
        for(int j=0;j<m;++j)
        {
            if(i>>j&1)
            {
                ++cnt;
                if((LL)t*p[j]>n)
                {
                    t=-1;
                    break;
                }
                t*=p[j];
            }
        }
        if(t==-1)
            continue;
        if(cnt%2)
            res+=n/t;
        else
            res-=n/t;
    }
    cout<<res<<endl;
    return 0;
}

博弈论

\[\begin{align} &对于公平组合组合游戏(ICG)\\ &若一个游戏满足:\\ &①.有两名玩家交替行动；\\ &②.在游戏进行任意时刻，可以执行的合法行动与轮到哪名玩家无关；\\ &③.不能行动的玩家判负.\\ &则称该游戏为公平组合游戏.\\ &NIM属于公平组合游戏. \end{align} \]

\[\begin{align} &在NIM游戏中两名玩家轮流选取任意数量的石子(不可以不选)，最终谁无法进行操作判负.\\ &那么就有两种情况:\ 先手必胜以及先手必败.(另每堆石子个数为a_i，假设有n堆石子，1\leq i\leq n)\\ &当下一步可以走到一个先手必败的状态时，那么此人先手必胜，当走不到任何一个先手必败的状态时，此人先手必败\\ &当满足\ a_1\bigoplus a_2\bigoplus \cdots\cdots\bigoplus a_n=0时先手必败.(\bigoplus为异或)\\ &当满足\ a_1\bigoplus a_2\bigoplus \cdots\cdots\bigoplus a_n \ !=0时先手必胜.\\ &先手必胜证明:假设a_1\bigoplus a_2\bigoplus \cdots\cdots\bigoplus a_n=x;x的二进制最高位的1为第k位，那么一定存在a_i的第k位为1\\ &那么a_i^x<a_i，将a_i这堆石子拿走a_i-(a_i\bigoplus x)个石子，拿走之后第a_i堆石子数会变成a_i\bigoplus x个石子，那么此时\\ &可以发现剩下的石子个数异或值为0，变成了先手必败的状态则得证.\\ &当开始一个石子都没有时:0\bigoplus 0\cdots\bigoplus 0=0，此时必败.\\ &当a_1\bigoplus a_2\bigoplus \cdots\cdots\bigoplus a_n=0时，利用反证法，假设从a_i堆中拿取完石子后剩余石子数位a_i'\\ &并且可以转换到先手必败的状态，那么a_1\bigoplus a_2\bigoplus \cdots \bigoplus a_i'\bigoplus\cdots\bigoplus a_n=0\\ &此时必须满足a_i=a_i'，但这与之相矛盾所以假设不成立.得证. \end{align} \]

/*
给定 n 堆石子，两位玩家轮流操作，每次操作可以从任意一堆石子中拿走任意数量的石子（可以拿完，但不能不拿），最后无法进行操作的人视为失败。
问如果两人都采用最优策略，先手是否必胜。
输入格式
第一行包含整数 n。
第二行包含 n 个数字，其中第 i 个数字表示第 i 堆石子的数量。
输出格式
如果先手方必胜，则输出 Yes。
否则，输出 No。
数据范围
1≤n≤105,
1≤每堆石子数≤109
输入样例：
2
2 3
输出样例：
Yes
*/
#include <iostream>
using namespace std;

int main()
{
    int n;
    scanf("%d",&n);
    int res=0;
    
    while(n--)
    {
        int x;
        scanf("%d",&x);
        res^=x;
    }
    if(res)
        puts("Yes");
    else
        puts("No");
    return 0;
}

\[\begin{align} &在博弈论中还有两个比较重要的东西Mex运算和SG函数.\\ &Mex运算用于求出集合中不存在的最小自然数，而假设一个状态后可转换到k个转台，\\ &则SG(y)=Mex(SG(y_1),SG(y_2),SG(y_3)\cdots\cdots SG(y_k)).\\ &当SG(x)=0时先手必败，SG(x)!=0时先手必胜.\\ &当有多个状态时,SG(1)\bigoplus SG(2)\bigoplus\cdots\cdots\bigoplus SG(n)=0时先手必败.\\ &SG(1)\bigoplus SG(2)\bigoplus\cdots\cdots\bigoplus SG(n)!=0时先手必胜.\\ &证明与NIM游戏的证明方法一致.\\ &后续例题使用到记忆化搜索请参考动态规划(DP). \end{align} \]

/*
给定 n 堆石子以及一个由 k 个不同正整数构成的数字集合 S。
现在有两位玩家轮流操作，每次操作可以从任意一堆石子中拿取石子，每次拿取的石子数量必须包含于集合 S，最后无法进行操作的人视为失败。
问如果两人都采用最优策略，先手是否必胜。
输入格式
第一行包含整数 k，表示数字集合 S 中数字的个数。
第二行包含 k 个整数，其中第 i 个整数表示数字集合 S 中的第 i 个数 si。
第三行包含整数 n。
第四行包含 n 个整数，其中第 i 个整数表示第 i 堆石子的数量 hi。
输出格式
如果先手方必胜，则输出 Yes。
否则，输出 No。
数据范围
1≤n,k≤100,
1≤si,hi≤10000
输入样例：
2
2 5
3
2 4 7
输出样例：
Yes
*/
#include <iostream>
#include <algorithm>
#include <cstring>
#include <unordered_set>
using namespace std;
const int N=110,M=10010;
int s[N],f[M];
int k,n;
int sg(int x);

int main()
{
    scanf("%d",&k);
    for(int i=0;i<k;++i)
    {
        scanf("%d",&s[i]);
    }
    
    memset(f,-1,sizeof f);
    
    scanf("%d",&n);
    int res=0;
    for(int i=0;i<n;++i)
    {
        int x;
        scanf("%d",&x);
        res^=sg(x);
    }
    if(res)
        puts("Yes");
    else
        puts("No");
    return 0;
}

int sg(int x)
{
    if(f[x]!=-1)
        return f[x];
    unordered_set<int> S;
    for(int i=0;i<k;++i)
    {
        int sum=s[i];
        if(x>=sum)
            S.insert(sg(x-sum));
    }
    for(int i=0;;++i)
    {
        if(!S.count(i))
        return f[x]=i;
    }
}