``# 二进制的数与位
在计算机的代码世界中,是以二进制的位的基础来组成数,至此我还是混淆,二级制的1000(十进制的8)中的1是第4个数字还是第3位数字
学过二进制的都知道,二级制只有0和1,通过2为底数,乘上幂计算得到的,其中幂的大小取决于在第几位,比如1000的1的幂的大小为3,则这个二级制位置的数值就为 \(2^3=8\)[1]
由2进制的计算方法,可以推理出n进制的计数方法,也就是位值计算法[2],这中计数法区别于我们的日常计数法。
日常的思维和计数法
为什么我们会把“514¥”念作“五百一十四 块钱”,而不是“五一四 块钱”呢?其实,念出“五百一十四”的时候,我们就已经进行了一遍以数值乘 10为底数幂为1-十、2-百的计算 然后加起来的过程
在这里个位数是第 1个数字,计算的过程是 四*1, 依次类推,整个计算的过程就是
五*100+一*十+四*1
所以我们从小开始思维一直就是以十进制来记忆,第 1个数字是个,第 2个数字是十,第 3个数字是百。
其实在学n进制之前,我们小学数学的十进制计数方法是按顺序记忆的[3],并没有指数和位值的说法。

n进制的位权
学了n进制之后,我们知道了, 底数的幂其实是 位权(weight),即“每位的权重”。
按照日常的思维,对于十进制来说,第\(i\)位的位权其实就是 \(10^{i-1}\),对于二进制来说,第\(i\)位的位权其实就是\(2^{i-1}\),一般的,对于n进制来说,第\(i\)位的位权其实就是\(n^{i-1}\)
还是五百一十四,四是第1位数字,位权其实就是\(10^0\)
但是按照计算机的思维和n进制的位权来定义,并不是这样的
打开微软自带的计算器软件,可以看到二进制的位置的标号
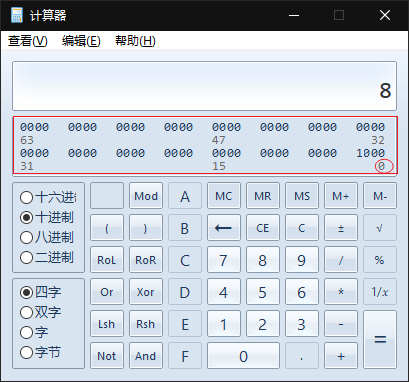
按照计算机的思维,第1个数字的标号是0,位权的公式正确的来说应该是\(10^{i}\),对于二进制来说,第\(i\)位的位权其实就是\(2^{i}\),一般的,对于n进制来说,第\(i\)位的位权其实就是\(n^{i}\)
总结
所以当五百一十四用计算机的思维,也就是十进制的说法的时候,其实四是第0位数字,而如果按照日常的思维来看四是第1个数字
按计算机思维,就是位值计数法,二级制的1000(十进制的8)中的1就是第3位数字,二级制而没有日常思维的计数方法,只需要把思维转变过来,就不会混淆了。
ps:我用了 个 来对应日常的思维,位来对应计算机思维。
数的产生和日常的十进制的历史发展
日常的十进制的历史发展和数的产生的历史发展更适合放在一块说
对于数字来说,主要的发展的历史就是[3:1]
原始人用石头一一对应数目
古代的古埃及象形数字,巴比伦楔形数字,古罗马数字,中国横纵式算筹代表特定的数目
现代的阿拉伯数字,也就是我们说的自然数
这些数的产生和十进制相关,人类在算数时普遍采用“十进制”这一体系,其背后的原因可能与人类拥有十根手指这一解剖学特征紧密相关。亚里士多德曾指出,人类对十进制的普遍使用,正是基于这样一个简单的解剖学事实:我们每个人都有十根手指。只不过,这些十进制记数体系并不是按位的,没有位值这个概念。[4]:
所以无论在那个时期的数字的进位和十都是联系紧密的,逢十进一的概念是日常习惯观念了,但是我们用位值(指数/幂)表示更多是在学了二进制之后,起码小学学数学的时候是没有提到的。
换个说法区分日常的十进制和n进制的十进制就是看是不是用位值(指数/幂)来计算
二进制的起源和计算机的历史发展
前面提到二进制是在计算机世界里面的,至于为什么会联系起来,就可以看看这个计算机宇宙的八卦
ps: 我在此之前对这些名人是一点不感冒的,但是成为圈里人(程序员)之后,再去看这些名人和发展历史就像八卦一样津津有味。或许历史就是当代人追八卦狂热了,用专业的笔墨记下事实,是不是学习历史的一个好方法就是成为圈里人。pps:记得我高一分文理科前,记忆力不好,但是历史分数好像还是不错的。
莱布尼茨:二进制的美妙的发源
在17世纪中叶,二进制由德国数学家戈特弗里德·威廉·莱布尼茨(德语:Gottfried Wilhelm Leibniz;1646年7月1日—1716年11月14日)在1703年发表的论文《论只使用符号0和1的二进制算术,兼论其用途及它赋予伏羲所使用的古老图形的意义》(Explication de l'arithmétique binaire, qui se sert des seuls caractères 0 et 1 avec des remarques sur son utilité et sur ce qu'elle donne le sens des anciennes figures chinoises de Fohy)
中系统地介绍了二进制数系统。[5]:
二进制的美妙不同于前面的用 数来描述生活的数目,而是用数学的符号和计算,描述人类全部思想领域的符号系统
这种思想是超前的,按照现在来看,不就是我们现在使用的计算机,用计算机语言表达出人类的思想领域的内容
当然莱布尼茨的二级制的启发也是有根据的,但是具体根据没有确认,不过这些依据的大体的思想表达都是相似的:
- 亚里士多德把概念分成固定的“范畴”[6]:
- 中国的八卦和《易经》中的二元思想
关于莱布尼茨的二级制的启发是不是受中国《易经》的启发,就像是网络热点惹人研究,网上可以看到很多人讨论[7],也有专业的去研究过,我也八卦了下。从参考文章来看确实有两个观点:
郭书春在《古代世界数学泰斗刘徽》一书461页中称:“中国有所谓《周易》创造了二进制的说法,至于莱布尼兹受《周易》八卦的影响创造二进制并用于计算机的神话,更是广为流传。事实是,莱布尼兹先发明了二进制,后来才看到传教士带回的宋代学者重新编排的《周易》八卦,并发现八卦可以用他的二进制来解释。”以此为由,认为并不是莱布尼茨看到阴阳八卦才发明二进制。梁宗巨著《数学历史典故》(1995年出版)一书14~18页对这一历史公案亦有此说。
胡阳、李长铎在《莱布尼茨发明二进制前没有见过先天图吗——对欧洲现存17世纪中西交流文献的考证》通过对欧洲现存17世纪中西交流文献的研究考证,否定了莱布尼茨在发明二进制以后才见到先天图的说法。先天图在莱布尼茨发明二进制之前,已被斯比塞尔称之为二进制。
其实按照参考文章的作者的观点更加好:
除了莱布尼茨个人的独创性的伟大贡献外,近代意义上的二进制实际上是“中西合璧”的产物[8]。
虽然莱布尼兹的论文提出了二进制可以作为新的计数方法,并可以完成基本的运算,但是却没有完成二进制的核心运算方法,也就是还没有找到用数学的符号描述人类思想的具体实现路径,直到布尔的研究发表。
布尔:从逻辑到代数
1854年,英国数学家乔治·布尔(英语:George Boole,1815年11月2日—1864年12月8日)发表了一篇里程碑式的论文,其中详细介绍了一种代数化的逻辑系统,后人称之为布尔代数。并在其代数中系统地应用了“真与假”的思想(即0与1)。
这里提到的代数就是也就是我们熟知的布尔运算(如与、或、非等),而逻辑就是人类概念的真假。
单从布尔运算来说,布尔的逻辑代数似乎是用一种特例的方式,描述人类思想领域的一角的真假逻辑而已。但二进制至此有了代数方法,数理逻辑从此就开始不断发展。
香农:数电之父
1937年,克劳德·香农(英语:Claude Elwood Shannon,1916年4月30日—2001年2月24日)在麻省理工大学完成了其电气工程硕士学位论文,用继电器和开关实现了布尔代数和二进制算术运算。论文题为《继电器与开关电路的符号分析》(A Symbolic Analysis of Relay and Switching Circuits),其中香农的理论奠定了数字电路的理论基础,香农凭这篇论文于1940年被授予美国阿尔弗雷德·诺贝尔协会美国工程师奖。哈佛大学的哈沃德·加德纳称,香农的硕士论文“可能是本世纪最重要、最著名的硕士学位论文”。[5:1]。
学电的都知道有三大本书是基础:电路,模电,数电,现在来看最后一个数电其实就是源于香农的研究,所以我自愿称其为数电之父
ps 为啥我学的数电那么厚一本,都不愿意搞个小节介绍下香农等前人的历史,不然我也不会提不起兴趣学习
我认为,香农的研究重要性是将电子器件完成了bool运算,意味着可以通过用电来控制计算,也就是自动化计算,也是计算机的实现的第一步。之后的就是各个计算机之父的诞生了。
对于计算机的发展,各个计算机之父,还有第一台计算机之争等又是巨大的瓜,准备再起一篇文章记录下,下面介绍的是和二进制相关的科学家。
乔治·斯蒂比兹: 数字计算机之父
1937年11月,任职于贝尔实验室的乔治·斯蒂比兹发明了用继电器表示二进制的设备。它是第一台二进制电子计算机[5:2]。这个主要贡献是硬件计算机的研发。
冯·诺依曼:现代计算机之父
为了改进使用十进制的第一台通用计算机ENIAC,冯·诺依曼再1945年6月发表了一份关于EDVAC长达101页的报告,报告提出的冯·诺伊曼结构一直延续至今[9]。报告提出以二进制替代十进制,因电子元件的“双稳态”(开/关)天然匹配二进制逻辑。其“存储程序”设计(指令与数据共存于存储器)奠定现代计算机五大结构基础[10]。
一些思考
其实这个二进制的思考也是源于存储器的大小和二进制数字的大小,每次看到1024,4k,1g这样的数字,还是感到陌生并在cmd输入calc,看看不同进制下的数字大小。后续有空完善下计算机历史,和存储大小的探索笔记。





 浙公网安备 33010602011771号
浙公网安备 33010602011771号