逻辑回归

 

 序

作为一个程序员， 在最初看到“逻辑回归”, 英文Logistic Regression, 内心有很多疑惑和问题。

它跟 Logistic分布或Logistic函数有关吗？“逻辑”是一个普通的音译，还是特指逻辑（是，否）问题？毕竟这个话题实在讨论分类问题，逻辑是“是否” ， 那么Logistic 的意思是什么了？ 

它是一个回归方程吗？那回归什么呢？Logistic函数的参数？那不成了一个参数估计的问题了吗？ 回归,怎么回归？为什么很多文章都在讨论最大似然？ 那不是概率分布模型的参数估计的方法吗？但难道不是回归吗 ？

特下此文还解释这些迷惑，也同时梳理一下最近收集的知识，作为开博第一篇。

此文写的比较早，公式中的关于样本x的上标与下表不怎么符合惯例，但由于特殊原因无法修正， 特此说明下：

X_： 代表样本X 的第i个分量。

X^{(i)  :} 

1.　　逻辑和Logistic

逻辑

逻辑是个外来语，它是Logic的音译， Logistic 来自Logistic函数， 最初是一个英国牧师为了研究人口增长率建立的数学模型。他为这个模型取名为 “Logistic”， 那么他的这么名字是要跟“逻辑”和对数都相关或是那个更相关，不从得知。但把Logistic翻译成逻辑，无论从音译（Logistic和logic 是同根的），还是意译都还是合适的。 Logistic regression毕竟是一个解决逻辑的模型：将随机事件归类成两类：1类和0类 。

1.1.　　Logistic 函数

 

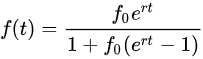
 分别取区间上一些不同的值的情况下随时间的变化情况

 

  

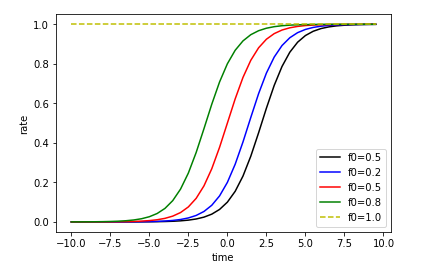
1.2.　　Logistic 分布

累计分布函数（CDF）=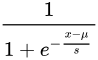 

分布图形 （u=0， s=1）：

  

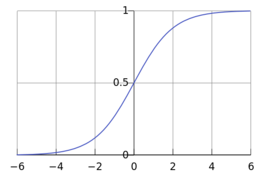
2.　　Logistic 回归模型

2.1.　　线性回归模型

逻辑（Logistic） 回归模型是一种通过样本点的属性和标签，建立的二分类模型。模型的输入样本点的所有基本属性（多个），和标签属性（一个）。如果我们把用于模型训练的每一个样本作为一个随机事件，基本属性是随机事件的条件，标签属性是随机事件的结果。

比如投硬币事件如果跟天气，地点，和时间有关系的话，天气，地点，和时间是基本属性，投硬币的结果是标签属性（正面：1，反面：0） 。

再比如年底升职事件如果跟平时的业绩绩效的级别，公司的年度利润率，老板的喜欢指数，在群众中的受欢迎指数的有关系的话，绩效的级别，年度利润率这些是基本属性，升职事件的结果是标签属性（升：1，不升：0） 。

那么看起来这是一个从若干条件属性到结果属性的回归方程(假设有2个条件属性)：

线型(Linear)函数回归：

z=h(x)=θ₀ + θ₁x₁ + θ₂x₂ 

或多项式（Polynomial）函数的回归模型(假设有2次多项式是合适的)

z=h(x)=θ₀ + θ₁x₁ + θ₂x₂  + θ₃x₁x_{2 +}  θ₄x_1² + θ₅x_2² 

线型函数和多项式函数在几何表示上是平面或n维空间中的直线，曲线，平面或曲面。那么这些线，面（在拟合之后）能最大程度的将空间中的点，分割成两部分：

在线、面一侧的点归为一类，另一侧为为第二类。形象如下面的样子：直角坐标系的两轴为基本属性，颜色代表标签属性，分割线为目标的n次多项式曲线。

逻辑回归的本质是求得分割线（z=0），分割线上方（z值>0)的点属于第一类，曲线下方（z值<0)的点属于第二类， 从而我们可以使用这个模型去预测新样本的分类。

分割线形如

θ₀ + θ₁x₁ + θ₂x_{2 =0}

θ₀ + θ₁x₁ + θ₂x₂  + θ₃x₁x_{2 +}  θ₄x_1² + θ₅x_2² =0

 

 

 

 

这就是逻辑回归吧：用回归的方法来解决逻辑的问题，把这个回归方程用样本拟合了不就done了吗？跟Logistic没什么关系了吗？

 

事实上，上述的线型回归或多项式回归的函数是很难拟合的，或者说直接拟合难以达到目标分割线的拟合度（fitness）。 只要是因为他们的值域都是无限发散的 （-∞，+∞ ），而真实（样本标签的）值域是非常有限收敛的：就离散的两个值：1和0 。而拟合的原理是同过某些过程（如最小二乘）求得拟合参数（θ₀,θ₁,..,θ_n)使代价函数达到它的最小值。 代价函数通常是被拟合的函数的值与样本真实值的差平方的平均值：如下。

 请注意代价函数J（θ）是一个关于θ的2次函数，x,y 是有限个离散的样本和样本标签的输入，x,y是常数 。y ⁽ⁱ⁾  是第i个样本的真值（标签）， x⁽ⁱ⁾为第i个样本。

使代价函数达到它的最小值，就是当1阶导数为零 是，函数到达最小值。

 2次函数是一个杯口向上（当样本值（x）都大于零）底部收敛的曲线或曲面，求得最底部的θ，就能使代价函数最小化。感觉有道理啊，至少对于当样本值（x）都大于零的情况，实际上是不然的。

看下面最简单的例子：样本属性只有一个（x1). 一部分样本的标签为0， 一部分样本的标签为1。 如果我们用上述的线型回归方法会求得蓝色的回归线，显然它不是我们期待的分割线 （分割线是z值为0）。

橘色的线是分割线，上述的回归方法是无法求得橘色线的。

 

 

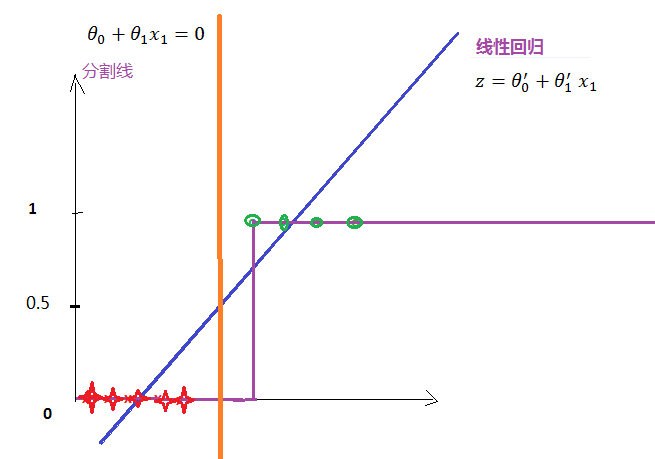
上述方法试图用简单的利用线性回归来解决分类的问题， 想法是对的， 但模型是错误的。 如果一定要是要使用线性回归模型，请参考感知机模型。 下面开始介绍逻辑回归模型。

2.2.　　逻辑回归模型

2.2.1. 模型

Sigmoid 函数：

 

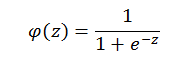
  Sigmoid函数是Logistic 函数的一个特例：当f0=0.5, r=0.0时。

同时也是Logistic 累计分布函数：但u=0, s=1

所以 Sigmoid函数拥有跟很大多数Logistic函数一样形态的曲线。重新贴一下Logistic函数的迷人曲线。 这个迷人曲线不仅能将一个无限发散的定义域（-∞，+∞ ）转化成收敛的值域，而且收敛的值域恰好是（0，1）：累计概率函数（CDF）的值域。

 

将线型函数h(x)sigmoid 化，得到：

 

 

或者将多线式函数h(x)sigmoid 化，得到：

 

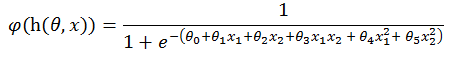
  将z函数（也就是h(θ，x)）sigmoid 化，得到的曲线（φ(z)）是形如下图绿色曲线，即逻辑回归曲线。 

  

 

 

当 z=0， φ(z)=0.5, 所有 φ(z)值小于0.5点属于一类， 所有 φ(z)值大于0.5点属于另一类。

下面的问题仿佛就是如何利用φ(z)的cost函数，通过最小化求得θ,则分割线即得。

 

2.2.2. 策略

策略是选择合适的代价函数，从而最优化代价函数构成的经验风险或结构化风险函数。

2.2.2.1.　　最小二乘风险函数

φ(z)的最小二乘cost 函数  为：

 

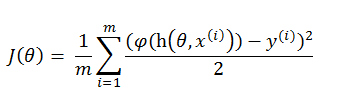
 这个函数的形如下曲线：他具有非突问题， 也就是有多个局部最低点，没有好办法求得全局最低点。

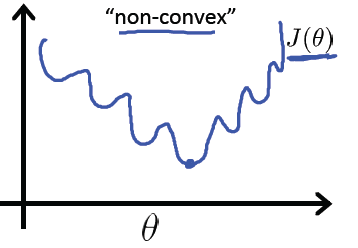
 我们期望形如下面的函数，只有一个全局最低点没，这样我们就就可以是使用梯度下降或牛顿方法求得全局最低点。

 

为了求得这样的凸性函数，需要一番数学推导了。

2.2.2.1.　　对数似然风险函数

 φ(z)函数在概率分布的角度来看上是，z值属于一类的条件概率， 可以记作：

可以写成一般形式： 

 从而我们可以用最大似然估计的方法求得θ， 是概率最大化， 以下为是求解过程。

将p(y|x;θ)代入最大似然公式：

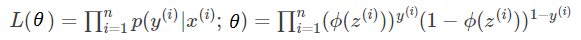
为了方便计算（乘法变加法），等式两边求log .

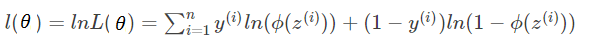
最大似然函数有大值不一定有最小值，而cost函数需要求最小值，为此只要将等式左右都加负号，使凸性反转。

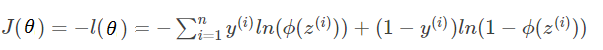
J(θ)的是型如下图的图形，符合我们期望的凸性函数。

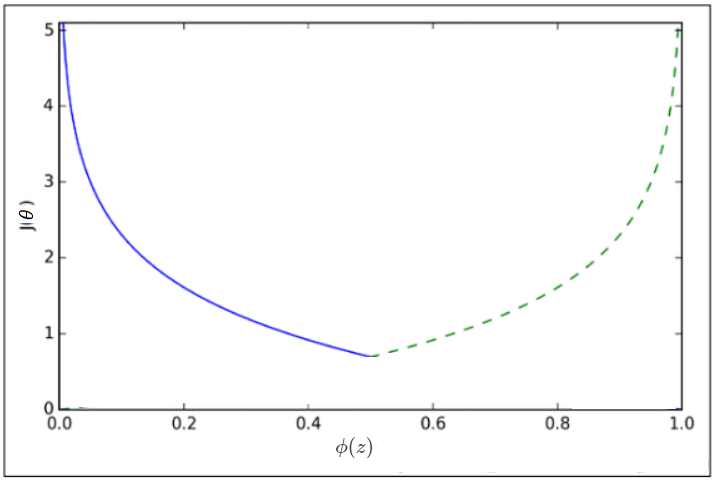
下面的问题就是要通过梯度下降的方法求得J(θ)下降到最低点的θ向量 。

 

2.2.3.　　梯度下降算法

我们使用梯度下降的算法来解决上述的优化问题。

 梯度指的是J函数对于θ各个分量（θ_0，θ₁x_1，θ_2， ...）偏导数所组成的向量，下降指的是沿梯度的负方向下降。借用泰勒公式来说明这个过程。

，δ为在θ各个分量上的增量。θ和δ都是向量，

， 二者之间的内积为 ： a 两个向量的夹角，当a=π 时，即θ沿梯度负方向下降最快。

 即： 

梯度下降就是反复的使θ沿梯度负方向下降，直到cost 函数 （J(θ)）小于预订的某个最小值（如0.0000001）或迭代次数到达某个限定值 （如1000）。

 

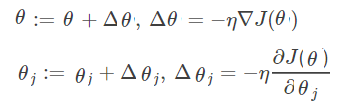
求一阶导数

Simoid函数有一个特性， 从而求导相对简单起来。

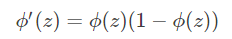
则：

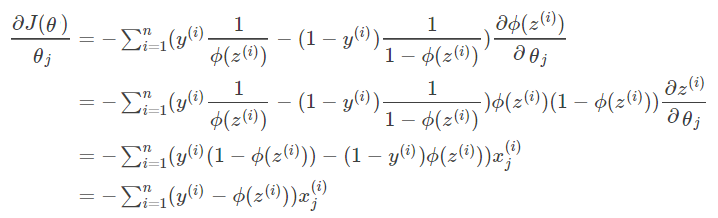
2.2.4.　　预测：

将x值代入φ(h(θ,x)中， 此h(θ,x)的参数θ通过梯度下降确定为常数。如果φ(h(θ,x)>0.5则为1类，否则为0类。

 

3.　　多项式的逻辑回归

3.1.　　正则化的风险函数

多项式模型比较复杂，比如2阶多项式需要6个θ分量，6阶多项式则需要48个θ分量 。它可以拟合非常复杂的分割线， 但同时也会有出现过拟合的问题 ：模型会尝试去兼顾各个测试数据点， 及时有些测试点明显是异常点。 这样曲线在某些小区间里的振动非常大， 也就是导数值（绝对值）非常大。 由于自变量值可大可小，只有系数足够大，才能产生大导数值， 这就是所谓的岭回归问题，如下图 。 如果发生过拟合时， 参数θ一般是比较大的值， 加入惩罚项后， 只要控制λ的大小，当λ很大时，θ1到θn就会很小，即达到了约束数量庞大的特征的目的。

 

 

 

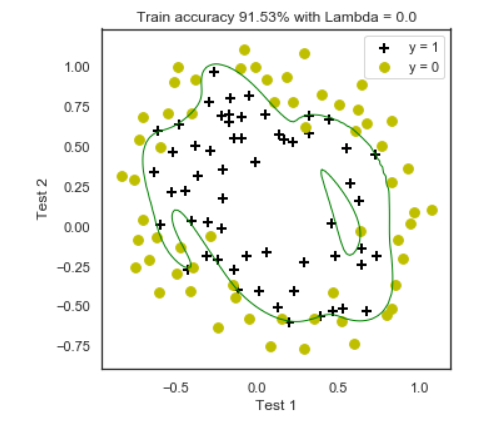
另外从贝叶斯的角度来分析， 正则化是为模型参数估计增加一个先验知识，先验知识会引导损失函数最小值过程朝着约束方向迭代。 L1正则是Laplace先验，L2是高斯先验。整个最优化问题可以看做是一个最大后验估计，其中正则化项对应后验估计中的先验信息，损失函数对应后验估计中的似然函数，两者的乘积即对应贝叶斯最大后验估计。

 

本例使用L2是高斯先验正则项 ： 假设θ符合（0,1/λ²）的正态分布 。

 

3.2.　　正则化梯度函数：

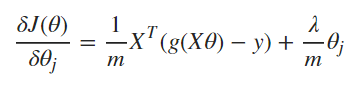
高斯先验正则项 推导

根据最大后验(MAP)估计 （来自于贝叶斯理论：P（θ|X）=P(X|θ）P(θ)/P(X) , 最大化L（θ） 省略了P（X）).

 

 ， m为样本个数， d是θ的维度 （多项式参数的个数）

 假设θ符合（0,τ²）的正态分布, 则

两边取对数：

变换成求最小值去掉常数项c：

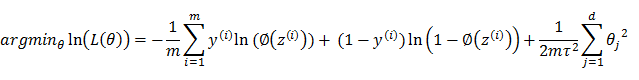
另 λ=1/(2τ² ) ^：

 

 

 

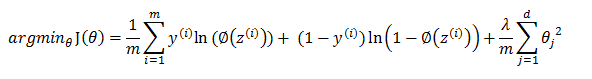
 参考

https://blog.csdn.net/han_xiaoyang/article/details/49123419，写的很牛的博客，本文的一些图例来自于此，该博文还有完整的python代码， 作者 寒小阳

https://blog.csdn.net/zjuPeco/article/details/77165974，也是一篇的很牛的博客 ，本文的一些数学推导来自于此，  作者 zjuPeco

《斯坦福大学公开课：机器学习》作者Andrew Ng， 老师的网易公开客，电脑看不了，只能通过手机， 非常牛。 

https://www.jianshu.com/p/a47c46153326， 写的很牛的博客，本文关于正则项的推理来自于此。 作者wujustin