概述:
一般使用的八大排序算法是:插入排序、选择排序、冒泡排序、希尔排序、归并排序、快速排序、堆排序、基数排序,每个方法有其适合的使用场景,可以根据具体数据进行选择.
几个概念:
内部排序:排序期间元素全部存放在内存中的排序;
外部排序:排序期间元素无法全部存放在内存中,必须在排序过程中根据要求不断地进行内外存之间移动地排序;
(这八种排序算法中除了多路归并排序是外部排序,其他都是内部排序)
稳定性:指的是经过排序后,值相同的元素保持原来顺序中的相对位置不变.
各算法时间复杂度、空间复杂度、所需辅助空间与稳定性如下:
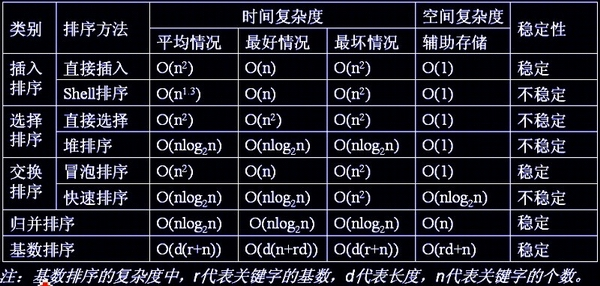
实现方法(这里都是进行从小到大的排序):
1.冒泡排序:
冒泡排序思想很简单,就是对每个下标i,取j从0到n-1-i(n是数组长度)进行遍历,如果两个相邻的元素s[j]>s[j+1],就交换,这样每次最大的元素已经移动到了后面正确的位置.
void bubbleSort(vector<int> &s){ for (int i = 0; i < s.size(); i++){ for (int j = 0; j < s.size() - 1 - i; j++){ if (s[j] > s[j + 1]) swap(s[j], s[j + 1]); } } }
冒泡排序的特点:稳定,每次排序后,后面的元素肯定是已经排好序的,所以每次排序后可以确定一个元素在其最终的位置上,冒泡排序比较次数:n(n-1)/2,移动次数:3n(n-1)/2.
2.插入排序:
插入排序又分为简单插入排序和折半插入排序;简单插入排序思想是每趟排序把元素插入到已排好序的数组中,折半插入排序是改进的插入排序,由于前半部分为已排好序的数列,这样我们不用按顺序依次寻找插入点,可以采用折半查找的方法来加快寻找插入点的速度.
简单插入排序:
void insertSort(vector<int> &s){ if (s.size() > 1){ for (int i = 1; i < s.size(); i++){ for (int j = i; j > 0 && s[j] < s[j - 1]; j--){ swap(s[j], s[j - 1]); } } } }
折半插入排序:
void binaryInsertSort(vector<int> &s){ int low, high, m, temp, i, j; for (i = 1; i < s.size(); i++){ //采用折半查找方法,寻找应该插入的位置 low = 0; high = i - 1; while (low <= high){ m = (low + high) / 2; if (s[m] > s[i]) high = m - 1; else low = m + 1; } //统一移动元素,将该元素插入到正确的位置 temp = s[i]; for (j = i; j > high + 1; j--){ s[j] = s[j - 1]; } s[high + 1] = temp; } }
插入排序的特点:
1.稳定;
2.最坏情况下比较n*(n-1)/2次,最好情况下比较n-1次;
3.第k次排序后,前k个元素已经是从小到大排好序的
3.简单选择排序:
选择排序思想是对每个下标i,从i后面的元素中选择最小的那个和s[i]交换.
void selectSort(vector<int> &s){ if(s.size()>1){ for(int i=0;i<s.size();i++){ int min=i; for(int j=i+1;j<s.size();j++){ if(s[j]<s[min]) min=j; } swap(s[i], s[min]); } } }
选择排序的特点:不稳定,每趟排序后前面的元素肯定是已经排好序的了,每次排序后可以确定一个元素会在其最终位置上.
4.快速排序:
快速排序是内排序中平均性能较好的排序,思想是每趟排序时选取一个数据(通常用数组的第一个数)作为关键数据,然后将所有比它小的数都放到它的左边,所有比它大的数都放到它的右边.
void quickSort(vector<int> &s, int low, int high){ if (low >= high) return; int l = low, r = high, val = s[low]; while (l < r){ while (l < r&&s[r] >= val) r--; if (l < r) s[l++] = s[r]; while (l < r&&s[l] <= val) l++; if (l < r) s[r--] = s[l]; } s[l] = val; quickSort(s, low, l - 1); quickSort(s, r + 1, high); }
快速排序的特点:
1.不稳定;
2.快速排序过程中不会产生有序子序列,但每一趟排序后都有一个元素放在其最终位置上;
3.每次选择的关键值可以把数组分为两个子数组的时候,快速排序算法的速度最快,当数组已经是正序或逆序时速度最慢;
4.递归次数与每次划分后得到的分区的处理顺序无关;
5.对n个关键字进行快速排序,最大递归深度为n,最小递归深度为log2n;
上面的快速排序算法是递归算法,非递归算法使用栈来实现:
//进行区域的划分 int partition(vector<int> &s, int low, int height){ int val = s[low]; while (low < height){ while (low < height&&s[height] >= val) height--; s[low] = s[height]; while (low < height&&s[low] <= val) low++; s[height] = s[low]; } s[low] = val; return low; } //排序 void quickSortNonRecursive(vector<int> &s, int low, int height){ stack<int> p; if (low < height){ int mid = partition(s, low, height); if (mid - 1 > low){ p.push(low); p.push(mid - 1); } if (mid + 1 < height){ p.push(mid + 1); p.push(height); } while (!p.empty()){ int qHeight = p.top(); p.pop(); int pLow = p.top(); p.pop(); int pqMid = partition(s, pLow, qHeight); if (pqMid - 1 > pLow){ p.push(pLow); p.push(pqMid - 1); } if (pqMid + 1 < qHeight){ p.push(pqMid + 1); p.push(qHeight); } } } }
5.希尔排序:
希尔排序是基于插入排序的一种排序算法,思想是对长度为n的数组s,每趟排序基于间隔h分成几组,对每组数据使用插入排序方法进行排序,然后减小h的值,这样刚开始时候虽然分组比较多,但每组数据很少,h减小后每组数据多但基本有序,而插入排序对已经基本有序的数组排序效率较高.
void shellSort(vector<int> &s){ int n = s.size(), h = 1; while (h < n / 3) h = 3 * h + 1; while (h >= 1){ for (int i = h; i < n; i++){ for (int j = i; j >= h && s[j] < s[j - h]; j -= h){ swap(s[j], s[j - h]); } } h /= 3; } }
希尔排序的特点:不稳定,每次排序后不能保证有一个元素在最终位置上
6.归并排序:
归并排序的思想是将两个有序表合并成一个新的有序表,即把待排序序列分为若干个子序列,每个子序列是有序的。然后再把有序子序列合并为整体有序序列。即先划分为两个部分,最后进行合并。
const int maxn=500000,INF=0x3f3f3f3f; int L[maxn/2+2],R[maxn/2+2]; void merge(vector<int> &a,int n,int left,int mid,int right){ int n1=mid-left,n2=right-mid; for(int i=0;i<n1;i++) L[i]=a[left+i]; for(int i=0;i<n2;i++) R[i]=a[mid+i]; L[n1]=R[n2]=INF; int i=0,j=0; for(int k=left;k<right;k++){ if(L[i]<=R[j]) a[k]=L[i++]; else a[k]=R[j++]; } } void mergesort(vector<int> &a,int n,int left,int right){ if(left+1<right){ int mid=(left+right)/2; mergesort(a,n,left,mid); mergesort(a,n,mid,right); merge(a,n,left,mid,right); } }
归并排序特点:稳定,可以用在顺序存储和链式存储的结构,时间复杂度在最好和最坏情况下都是O(nlogn)
7.堆排序:
堆排序是基于选择排序的一种排序算法,堆是一个近似完全二叉树的结构,且满足子结点的键值或索引总是小于(或者大于)它的父节点。这里采用最大堆方式:位于堆顶的元素总是整棵树的最大值,每个子节点的值都比父节点小,堆要时刻保持这样的结构,所以一旦堆里面的数据发生变化,要对堆重新进行一次构建。
void max_heapify(vector<int> &arr, int start, int end) { //建立父节点指标和子节点指标 int dad = start; int son = dad * 2 + 1; while (son <= end) { //若子节点指标在范围内才做比较 if (son + 1 <= end && arr[son] < arr[son + 1]) //先比较两个子节点大小,选择最大的 son++; if (arr[dad] > arr[son]) //如果父节点大於子节点代表调整完毕,直接跳出函数 return; else { //否则交换父子内容再继续子节点和孙节点比较 swap(arr[dad], arr[son]); dad = son; son = dad * 2 + 1; } } } void heap_sort(vector<int> &arr, int len) { //初始化,i从最後一个父节点开始调整 for (int i = len / 2 - 1; i >= 0; i--) max_heapify(arr, i, len - 1); //先将第一个元素和已经排好的元素前一位做交换,再从新调整(刚调整的元素之前的元素),直到排序完毕 for (int i = len - 1; i > 0; i--) { swap(arr[0], arr[i]); max_heapify(arr, 0, i - 1); } }
堆排序特点:不稳定,最坏,最好,平均时间复杂度均为O(nlogn)
8.基数排序:
基数排序是一种非比较型整数排序算法,其原理是将数据按位数切割成不同的数字,然后按每个位数分别比较,在类似对百万级的电话号码进行排序的问题上,使用基数排序效率较高
//寻找数组中最大数的位数作为基数排序循环次数 int KeySize(vector<int> &s, int n){ int key = 1; for (int i = 0; i < n; i++){ int temp = 1; int r = 10; while (s[i] / r > 0){ temp++; r *= 10; } key = (temp > key) ? temp : key; } return key; } //基数排序 void RadixSort(vector<int> &s, int n){ int key = KeySize(s, n); int bucket[10][10] = { 0 }; int order[10] = { 0 }; for (int r = 1; key > 0; key--, r *= 10){ for (int i = 0; i < n; i++){ int lsd = (s[i] / r) % 10; bucket[lsd][order[lsd]++] = s[i]; } int k = 0; for (int i = 0; i < 10; i++){ if (order[i] != 0){ for (int j = 0; j < order[i]; j++) s[k++] = bucket[i][j]; } order[i] = 0; } } }
基数排序特点:稳定,时间复杂度为O (nlog(r)m),其中r为所采取的基数,而m为堆数,在某些时候,基数排序法的效率高于其它的稳定性排序法。
部分参考:百度百科、微信公众号这或许是东半球分析十大排序算法最好的一篇文章https://mp.weixin.qq.com/s/Qf416rfT4pwURpW3aDHuCg




 浙公网安备 33010602011771号
浙公网安备 33010602011771号