有进度条圆周率运算

圆周率计算分析

方法：蒙特卡落法（随机抽样技术，是一种随机模拟方法，以概率和统计理论方法为基础的一种计算方法。是使用随机数（或更常见的伪随机数）来解决很多计算问题的方法)

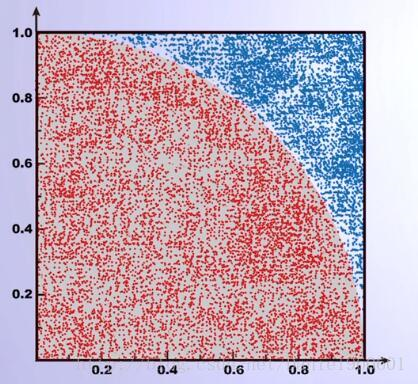
一正方形中构造四分之一个圆，随机撒点，根据点到原点的距离判断点是落在1/4的圆内还是在圆外，从而根据落在两个不同区域的点的数目，求出两个区域的比值。

代码

 1 from random import random
 2 from time import perf_counter
 3 DARTS = 1000*1000
 4 hits = 0.0
 5 start = perf_counter()
 6 for i in range(1,DARTS+1):
 7     x,y = random(),random()
 8     dist = pow(x**2 + y**2,0.5)
 9     if dist <=1.0:
10         hits = hits + 1
11 pi = 4 * (hits/DARTS)
12 end = perf_counter()
13 print("圆周率值是:{}".format(pi))
14 print("运行时间是:{:.5f}s".format(end-start))
CalPiV1

 

结果

加大难度~

含时间进度条的圆周率计算（同样以蒙特卡罗法为思想进行计算）

 1 from random import random
 2 from time import perf_counter
 3 import time
 4 scale = 50
 5 print("执行开始".center(scale//2,"-"))
 6 DARTS = 1000*1000
 7 hits = 0.0
 8 start = perf_counter()
 9 for i in range(1,DARTS+1):
10     x,y = random(),random()
11     dist = pow(x**2 + y**2,0.5)
12     if dist <=1.0:
13         hits = hits + 1
14 pi = 4 * (hits/DARTS)
15 for i in range(scale+1):
16     a = '*' * i
17     b = '.' * (scale-i)
18     c = (i/scale)*100
19     dur = time.perf_counter() - start
20     print("\r{:.2f}s[{}->{}]{:^3.0f}%".format(dur,a,b,c))
21     time.sleep(0.1)
22 print("\n圆周率值是:{:6f}".format(pi))
23 print("执行结束".center(scale//2,"-"))
CalPiV2

 

代码（将打印时间进度条代码中最后的end=""删除会更好哦,效果图如下)

 

 

 

posted @ 2020-03-19 22:11  Ni__23  阅读(163)  评论(0)    收藏  举报