【 乱搞 】正确姿势的乱搞--模拟退火
模拟退火大概原理就是将热力学里面金属退火的原理放在了统计学意义中。
其在计算机科学中的应用也是很可观的---处理一些无法用多项式时间复杂度解决的np问题。
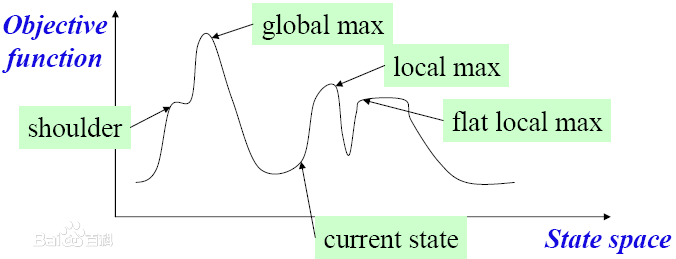 如果这个函数满足单峰性,我们往往可以直接套用三分来处理,但是都说了这如果是一个奇怪的函数,有很多个峰怎么办呢?
有一个神奇的贪心算法叫做爬山。每次随机一个delta值,并且每次值随机范围越变越小,看一下变化这个delta值之后的值是否更好,更好就爬山爬过去。
这个算法很容易陷入一个区间内的极优值,而无法到底最终的最优值。
那么退火来了!
如果这个函数满足单峰性,我们往往可以直接套用三分来处理,但是都说了这如果是一个奇怪的函数,有很多个峰怎么办呢?
有一个神奇的贪心算法叫做爬山。每次随机一个delta值,并且每次值随机范围越变越小,看一下变化这个delta值之后的值是否更好,更好就爬山爬过去。
这个算法很容易陷入一个区间内的极优值,而无法到底最终的最优值。
那么退火来了!
引入
对于一些最优化问题,往往我们可以转化为一个神奇的函数(参数不限),比如像这样 如果这个函数满足单峰性,我们往往可以直接套用三分来处理,但是都说了这如果是一个奇怪的函数,有很多个峰怎么办呢?
有一个神奇的贪心算法叫做爬山。每次随机一个delta值,并且每次值随机范围越变越小,看一下变化这个delta值之后的值是否更好,更好就爬山爬过去。
这个算法很容易陷入一个区间内的极优值,而无法到底最终的最优值。
那么退火来了!
如果这个函数满足单峰性,我们往往可以直接套用三分来处理,但是都说了这如果是一个奇怪的函数,有很多个峰怎么办呢?
有一个神奇的贪心算法叫做爬山。每次随机一个delta值,并且每次值随机范围越变越小,看一下变化这个delta值之后的值是否更好,更好就爬山爬过去。
这个算法很容易陷入一个区间内的极优值,而无法到底最终的最优值。
那么退火来了!
原理
物理学得差就不讲物理上的原理了orz. 百度百科走你实现
首先我们设定一个初始温度,初始点,降温系数和最终温度,初始温度要保证覆盖完可能是最优点的范围,降温系数略比1小一点。 之后我们每次从当前点位置进行随机新位置,并且这个随机的范围与当前温度$T$正相关,之后看一下那个位置的函数对应的值$f(new)$,与当前位置$f(old)$相比可以得到差值$\Delta = f(now) - f(old)$ 比如我们要求函数最小值,那么当前位置转移过去的概率为 $ \begin{cases} 1, & {if \Delta < 0} \ e^{-\Delta/T}, &{if \Delta>0} \end{cases} $ 这个如果$\Delta<0$应该都能理解,关于大于0,是根据Metropolis接受准则来的。感性理解就好,这样就可以以一定概率接受一个更差解,并且最终的概率是收敛的,因此这个算法是真实可行的。参数
退火系数设为略小于1的正数,大概0.98再往上取。最后为了保证答案质量可以等温度降完之后再在答案点附近多随几下。如果要保证时间,可以用用蒙特卡罗卡时。 随机数种子取多少?嘿嘿嘿嘿嘿 [JSOI2004]平衡点 正解是半平面交切割凸包?orz直接裸上模拟退火orz#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<cstdlib>
#include<ctime>
typedef double db;
const db JW = 0.98;//降温系数
const db eps = 1e-3;//精度误差以及最后的终止温度
using namespace std;
struct nod{
db x,y,g;
}z[1005];
nod ANS,NOW; db minans = 1e100;
int n;
db calc(nod o) {
db res = 0;
for(int i=1;i<=n;i++) {
res += sqrt( (z[i].x-o.x)*(z[i].x-o.x) + (z[i].y-o.y)*(z[i].y-o.y) )*z[i].g;
}
if(res<minans) minans = res , ANS = o;
return res;
}
db getrd() {
return 1.0*rand()/RAND_MAX;
}
void SA(db T) { //初始温度
NOW = ANS;
db nowj = calc(NOW);//当前点的解
while(T>eps) {
nod tmp;
tmp.x = NOW.x + T*(getrd()*2-1.0);
tmp.y = NOW.y + T*(getrd()*2-1.0);
db tmpj = calc(tmp);
db delta = tmpj - nowj;
if(delta<0||(exp(-delta/T))>getrd()){ //根据Metropolis准则有一定概率接受更差解
NOW = tmp; nowj = tmpj;
}
T = T*JW;
}
//为保证最终答案质量在答案点附近多随几次
for(int i=1;i<=1000;i++) {
nod tmp;
tmp.x = ANS.x + T*(getrd()*2-1.0);
tmp.y = ANS.y + T*(getrd()*2-1.0);
calc(tmp);
}
}
int main() {
srand(19260817);//神秘质数
scanf("%d",&n);
for(int i=1;i<=n;i++) {
scanf("%lf%lf%lf",&z[i].x,&z[i].y,&z[i].g);
ANS.x += z[i].x; ANS.y += z[i].y;
}
ANS.x/=n; ANS.y/=n;
SA(20000);
printf("%.3f %.3f",ANS.x,ANS.y);
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号