【清华集训2015]静态仙人掌】仙人掌剖分

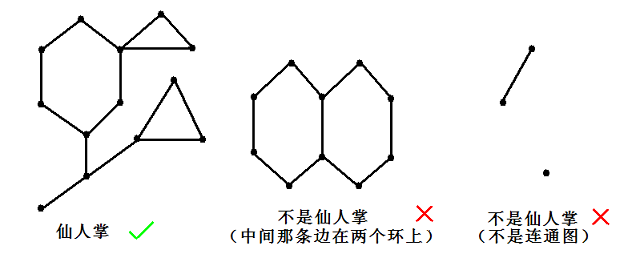毒瘤仙人掌，明明放到树上一道板题的非要构造到仙人掌上来出题orz orz orz orz orz 在OI的上古时代，流传着这样一个故事：有一天，小W到森林里游玩，回来之后跟小V说，我发现好多棵会动的树耶！小V说，这有什么好稀奇的，我用手指头就能维护每棵树的形态。于是又过了几天小W到沙漠里游玩，回来之后跟小V说，我发现好多棵会动的仙人掌耶！小V说，这有什么好稀奇的，我用脚丫子就能维护每棵仙人掌的形态。小S看到了这段故事，深受感动。他决定一步步做起，从仙人掌做起，从不会动的仙人掌做起。本题中，我们定义：什么是仙人掌

如果一个无向连通图的任意一条边最多属于一个简单环，且不存在自环，我们就称之为仙人掌。仙人掌上的两点间最短路径（一定是简单路径）与最长简单路径的定义与一般无向图的定义相同。本题中，我们还保证任何一个简单环的长度均为奇数。这意味着不存在重边，并且任意两点间的最短路径与最长简单路径一定是唯一的。为了证明你确实能够维护仙人掌，我们给你 $n$ 个结点，从 $1$ 到 $n$ 标号，其中 $1$ 号点是仙人掌的根。它有 $m$ 条边，第 $i$ 条边连接了结点 $u_i$ 与 $v_i$。每个结点有一个颜色（黑或白），初始时均为黑色。现在有 $q$ 次操作，每次操作格式为 $op$ $x$（$1 \leq op \leq 3, 1 \leq x \leq n$）：

若$op=1$，表示将点$x$到根的最短路径上的所有点的状态取反（黑变白，白变黑）；
若$op=2$，表示将点$x$到根的最长简单路径上的所有点的状态取反；
若$op=3$，表示询问点$x$的子仙人掌中的黑点数目。点 $x$ 的子仙人掌定义为：删除从根到点 $x$ 的所有简单路径上的所有边后，点 $x$ 所在的连通块。

输入格式

第一行三个用空格隔开的正整数 $n,m,q$ 表示一共有 $n$ 个结点，$m$ 条边，$q$ 个操作。接下来 $m$ 行，每行两个空格隔开的正整数 $u_i, v_i$，表示一条边。接下来 $q$ 行，每行表示一个操作，格式如上述。

输出格式

对于每个 $op=3$ 的操作，输出一行相应的结果。

样例一

input

output

样例二

见样例数据下载。这组数据符合子任务4的限制与约定。

样例三

见样例数据下载。这组数据符合子任务5的限制与约定。

样例四

见样例数据下载。这组数据符合子任务6的限制与约定。

限制与约定

本题使用捆绑测试。每个子任务有若干个测试点，分为 $8$ 个子任务，你只有通过一个子任务的所有测试点才能得到这个子任务的分数。

前七个子任务的限制

时间限制：$1\texttt{s}$。 空间限制：$768\texttt{MB}$。 $n, q \leq 50000$。

子任务1（7分）

$n \leq 2, q \leq 2000$。

子任务2（14分）

$n \leq 20, q \leq 2000$。

子任务3（9分）

$n, q \leq 2000$。

子任务4（17分）

保证 $m=n-1$，并且 $u_i=i,v_i=i+1$，且不存在 $op=2$ 的操作。

子任务5（14分）

保证 $m=n-1$，并且 $u_i < v_i$，且不存在 $op=2$ 的操作。

子任务6（11分）

保证不存在 $op=2$ 的操作。

子任务7（18分）

没有特殊的限制与约定。

子任务8（10分）

空间限制缩小为 $128\texttt{MB}$。我们发现，如果这只是一棵树，嘿嘿嘿，那不就是裸的树剖吗。可惜他是一个仙人掌。那么我们就利用圆方树来进行仙人掌剖分。对于仙人掌的剖分不能按照树一样直接剖，考虑到我们可能应该在同一个环上的点剖在一起。那么就这样处理-->我们把所有的点分成三类点：0,在链上的点（除了１号点外不包括链根）1.在环上并且处于从重儿子到环根最短路径上 2,在环上并且处于从重儿子到环根的长路径上。我们在树剖的时候，如果遇到圆点继续剖下去，遇到方点，将环按照环序加入到树剖序中（在这里我们都不考虑作为方点父亲的那一个圆点），并且跳过重儿子，之后再进行剖，并且给环上所有点记录下类型，然后继续剖。圆点树剖记得子树(仙人掌)范围,方点记录轻环儿子的范围。线段树维护3种点黑点的和个数,带lazy下放。查询就直接查询那个点和那个点的子仙人掌。修改的时候跳一跳，发现top是方点(说明是从方点的重儿子跳过来的)，直接修改。如果top是圆点(说明到达top的父亲方点的环的轻儿子)，稍微特殊处理一下就好了。 code:

#include<stdio.h>
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cmath>
using namespace std;
const int maxn = 2e5+5;
/*
0 the point on the line
1 the sort point on the cir
2 the long point on the cir
*/
struct edge{
    int en[maxn],nt[maxn],la[maxn],owo;
    void adg(int x,int y) {
        en[++owo]=y; nt[owo]=la[x]; la[x]=owo;
    }
}V,G;
int n,m,q,scc;
struct ddd{
    int l,r;
}pos[maxn];
int kind[maxn];

namespace tajan{
    int low[maxn],dfn[maxn],dfx,sta[maxn],top;
    void tarjan(int x) {
            low[x] = dfn[x] = ++dfx;
            sta[++top] = x;
            for(int it=V.la[x];it;it=V.nt[it]) {
            int y = V.en[it];
            if(!dfn[y]) {
                tarjan(y); low[x] = min(low[x],low[y]);
                if(low[y]>=dfn[x]) {
                    ++scc; int o;
                    do{
                        o = sta[top--];
                        G.adg(scc,o);
                    }while(o!=y);
                    G.adg(x,scc);
                }
            } else low[x] = min(low[x],dfn[y]);
        }
    }
}


int top[maxn],siz[maxn],dis[maxn],zerz[maxn],ID[maxn],DY[maxn],tot,fa[maxn];

void Dfsgsz(int x,int ba) {
    siz[x] = 1; fa[x] = ba;
    for(int it=G.la[x];it;it=G.nt[it]) {
        int y = G.en[it];
        if(y==ba) continue;
        Dfsgsz(y,x);
        siz[x] += siz[y];
        if(siz[y]>siz[zerz[x]]) zerz[x] = y;
    }
}

void Dfsgps(int x,int ace) {
    top[x] = ace;
    if(x<=n) {
        pos[x].l = tot+1;
        if(!zerz[x]) { pos[x].r = tot; return; }
    } else {
        ++tot; pos[x].l  = tot + 1;
        ID[x] = tot; DY[tot] = x;
        for(int it=G.la[x];it;it=G.nt[it]) {
            dis[x]++; dis[G.en[it]] = dis[x];
        }
        dis[x]++; kind[x] = 0;
        int pp = (dis[zerz[x]] <= (dis[x]>>1) )?1:2;
        for(int it=G.la[x];it;it=G.nt[it]) {
            int y = G.en[it];
            if(y==zerz[x]) pp = 3 - pp;
            else {
                ++tot; ID[y] = tot; DY[tot] = y; kind[y] = pp;
            }
        }
        pos[x].r = tot;
        ++tot; ID[zerz[x]] = tot; kind[zerz[x]] = 0; DY[tot] = zerz[x];
    }
    Dfsgps(zerz[x],ace);
    for(int it=G.la[x];it;it=G.nt[it]) {
        int y = G.en[it];
        if(y==zerz[x]) continue;
        Dfsgps(y,y);
    }
    if(x<=n) pos[x].r = tot;
}
namespace seg{
    struct node{
        node *ls,*rs;
        int pt[3],sm[3],laz[3];
    }z[maxn],*rt; int tot;
    void chan(node *&p,int c) {
        p->laz[c]^=1; p->sm[c] = p->pt[c] - p->sm[c];
    }
    void ptd(node *&p) {
        if(p->ls==NULL) return;
        for(int i=0;i<=2;i++) {
            if(p->laz[i]) {
                chan(p->ls,i); chan(p->rs,i); p->laz[i] = 0;
            }
        }
    }
    void upd(node *&p) {
        for(int i=0;i<=2;i++) {
            p->sm[i] = p->ls->sm[i] + p->rs->sm[i];
        }
    }
    void maketree(node *&p,int l,int r) {
        p = &z[++tot];
        if(l==r) {
            if(DY[l]<=n) {
                int oo = kind[DY[l]];
                p->pt[oo] = p->sm[oo] = 1;
            }
            return;
        }
        int mid = (l+r)>>1;
        maketree(p->ls,l,mid); maketree(p->rs,mid+1,r);
        upd(p);
        for(int i=0;i<=2;i++) p->pt[i] = p->ls->pt[i] + p->rs->pt[i];
    }

    void changeall(node *&p,int l,int r,int x,int y) {
        if(x<=l&&r<=y) {
            chan(p,0); chan(p,1); chan(p,2);
            return;
        }
        ptd(p);
        int mid = (l+r)>>1;
        if(y<=mid) changeall(p->ls,l,mid,x,y);
        else if(x>mid) changeall(p->rs,mid+1,r,x,y);
        else changeall(p->ls,l,mid,x,y),changeall(p->rs,mid+1,r,x,y);
        upd(p);
    }
    void changekind(node *&p,int l,int r,int x,int y,int cc) {
        if(x<=l&&r<=y) {
            chan(p,cc); chan(p,0);
            return;
        }
        ptd(p);
        int mid = (l+r)>>1;
        if(y<=mid) changekind(p->ls,l,mid,x,y,cc);
        else if(x>mid) changekind(p->rs,mid+1,r,x,y,cc);
        else changekind(p->ls,l,mid,x,y,cc),changekind(p->rs,mid+1,r,x,y,cc);
        upd(p);
    }
    int getsumall(node *&p,int l,int r,int x,int y) {
        if(x<=l&&r<=y) return p->sm[0] + p->sm[1] + p->sm[2];
        int mid = (l+r)>>1;
        ptd(p);
        if(y<=mid) return getsumall(p->ls,l,mid,x,y);
        else if(x>mid) return getsumall(p->rs,mid+1,r,x,y);
        else return getsumall(p->ls,l,mid,x,y) + getsumall(p->rs,mid+1,r,x,y);
    }
}

void solve(int x,int op) {
    int xo;
    while(top[x]!=1) {
        xo = top[x];
        if(xo>n) {
            seg::changekind(seg::rt,1,scc,ID[xo],ID[x],op);
            x = fa[xo];
        } else {
            if(x!=xo) seg::changekind(seg::rt,1,scc,ID[zerz[xo]],ID[x],op);
            x = fa[xo];
            int inwel = (dis[xo]<=(dis[x]>>1) ) ? 1 : 2;
            if(inwel==op) {
                seg::changeall(seg::rt,1,scc,pos[x].l,ID[xo]);
                if(dis[zerz[x]]<=dis[xo]) seg::changeall(seg::rt,1,scc,ID[zerz[x]],ID[zerz[x]]);
            } else {
                seg::changeall(seg::rt,1,scc,ID[xo],pos[x].r);
                if(dis[zerz[x]]>dis[xo]) seg::changeall(seg::rt,1,scc,ID[zerz[x]],ID[zerz[x]]);
            }
        }
    }
    seg::changekind(seg::rt,1,scc,ID[1],ID[x],op);
}
int getans(int x) {
    return seg::getsumall(seg::rt,1,scc,ID[x],ID[x]) + ( (pos[x].l<=pos[x].r)?getsumall(seg::rt,1,scc,pos[x].l,pos[x].r) :0 );
}

int main() {
//  freopen("lover.txt","r",stdin);
    scanf("%d%d%d",&n,&m,&q);
    scc = n;
    for(int i=1;i<=m;i++) {
        int x,y; scanf("%d%d",&x,&y);
        V.adg(x,y); V.adg(y,x);
    }
    tajan::tarjan(1);
    Dfsgsz(1,0);
    top[1] = ID[1] = DY[1] =  tot = 1;
    Dfsgps(1,1);
    seg::maketree(seg::rt,1,tot);
    for(int i=1;i<=q;i++) {
//      cerr<<"fuck:"<<i<<endl;
        int op,x; scanf("%d%d",&op,&x);
        if(op==1||op==2) solve(x,op);
        else printf("%d\n",getans(x));
    }
}

posted @ 2019-01-11 18:31 Newuser233 阅读(35) 评论(0) 收藏举报

刷新页面返回顶部

Newuser233

来自高中南开，大学华科的蒟蒻。qq:947534376 cf账号:newusers 个人主页 www.newuser.top 从wordpress刚转到cnblog，文章都还没有分类ovo