【[Code+#2]白金元首与独舞】矩阵树定理

然而并不清楚原理，只会背结论orz。。。 Luogu4033 元首把花园分为 $n$ 行 $m$ 列的网格。每个格子中都可以放置一个标识，指向上、下、左、右四个方向中的任意一个。元首位于一个格子时，会按照其中标识所指的方向进入周围的格子，或者走出花园（即目的格子不在网格之内）。举个例子 —— 对于下面的放置方式，元首从第 3 行第 2 列的格子开始，会沿着以红色标出的路径走出花园；从第 2 行第 2 列的格子开始，则会在以蓝色标出的环路内不断地行走。 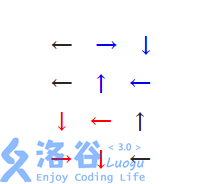元首已经设计好了大部分格子的标识。元首用字符 L、R、U、D 分别表示指向左、右、上、下四个方向的标识，用字符 . 表示未决定的格子。现在，元首希望将每个 . 替换为 L、R、U、D 中任意一种，使得从花园中的任意一个格子出发，按照上述规则行走，都可以最终走出花园。 你需要编写程序帮助元首计算替换的不同方案数。两个方案不同当且仅当存在一个格子，使得两个方案中该格子内的标识不同。当然，由于答案可能很大，只需给出方案数除以 10^9 + 7109+7所得的余数即可。

输入输出格式

输入格式： 从标准输入读入数据。 输入的第一行包含一个正整数 T —— 测试数据的组数。接下来包含 T 组测试数据，格式如下，测试数据间没有空行。 第 $1$ 行：两个空格分隔的正整数 n、m —— 依次表示花园被分成的行数和列数。 接下来 n 行：每行一个长度为 m 的由字符 L、R、U、D 和 . 组成的字符串 —— 表示花园内已经确定的格子状态。 输出格式： 输出到标准输出。 对于每组测试数据输出一行 —— 满足条件的方案数除以 10^9 + 7所得的余数。

输入输出样例

输入样例#1： 复制

5
3 9
LLRRUDUUU
LLR.UDUUU
LLRRUDUUU
4 4
LLRR
L.LL
RR.R
LLRR
4 3
LRD
LUL
DLU
RDL
1 2
LR
2 2
..
..

输出样例#1： 复制

3
8
0
1
192

说明

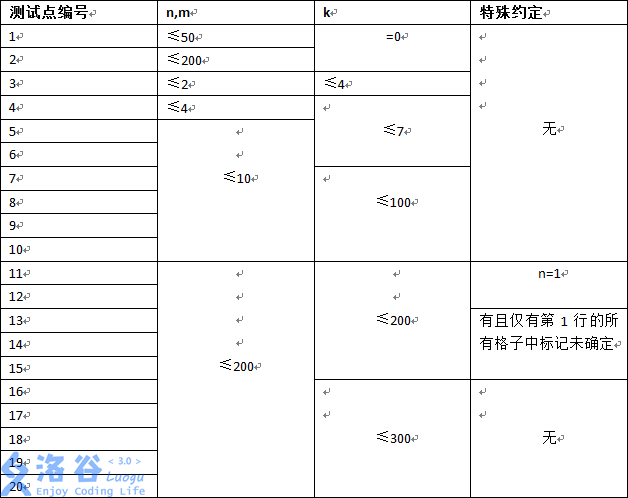
样例解释 第 1 组数据中，将惟一的 . 替换成 R、U 或 D 均满足要求。 第 2 组数据中，将左上方和右下方的两个 . 分别替换成 LR、LU、LD、UR、UU、UD、DR 或 DD 均满足要求。 第 3 组数据中，没有待决定的格子，原本的安排会使得元首陷入无尽的环路，故答案为 $0$。该组数据与题目描述中的例子相同。 第 4 组数据中，也没有待决定的格子，但原本的安排已经满足要求，故答案为 $1$。 令 $k$ 表示标记未确定（即包含 “.”）的格子总数。 对于所有数据，有$1\le T\le 10$，$1\le n,m\le 200$，$0\le k\le \min (nm,300)$。 我们对于方向超出去的建一个超级虚点，所有方向超出的点都实际指向虚点，对于所有不定向点向四周连边，然后跑一个有向图（内向外向都可以）的矩阵树定理就可以了。这样就可以过前50分。实际上我们发现我们只需要考虑那些不定向点和虚点就可以了。所有我们利用并查集找到某个点对应的第一个不定向点或者找到虚点，进行连边。这样就可以直接跑矩阵树了。 矩阵树定理结论：对于一张无向基尔霍夫矩阵（度数矩阵-邻接矩阵）然后以某个点为根的生成树个数就是他的余子式。对于有向图，若求以某点为根的内向树，则基尔霍夫矩阵为（出度矩阵-邻接矩阵），外向树（入度矩阵-邻接矩阵）。

#include<stdio.h>
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<vector>
#define pr pair<int,int>
#define fi first
#define se second
using namespace std;
const int maxn = 25;
const int mod = 1e9+7;
int mul(int x,int y) {
    return 1ll*x*y%mod;
}
int add(int x,int y) {
    x+=y; return x>=mod?x-mod:x;
}
int sub(int x,int y) {
    x-=y; return x<0?x+mod:x;
}
int inv(int a) {
    int b = mod-2,ans=1;
    for(;b;b>>=1,a=mul(a,a))
        if(b&1) ans = mul(ans,a);
    return ans;
}
int a[355][355];
int gauss(int n) {
    int mk = 1; int ans = 1;
    for(int i=2;i<=n;i++) {
        int id = -1;
        for(int j=i;j<=n;j++) {
            if(a[j][i]) {id=j; break;}
        }
        if(id==-1) return 0;
        if(id!=i) {
            mk^=1;
            for(int j=2;j<=n;j++) swap(a[i][j],a[id][j]);
        }
        int iv = inv(a[i][i]);
        for(int j=i+1;j<=n;j++) {
            if(a[j][i]) {
                int tmp = mul(a[j][i],iv);
                for(int k=2;k<=n;k++) {
                    a[j][k] = sub(a[j][k],mul(a[i][k],tmp));
                }
            }
        }
        ans = mul(ans,a[i][i]);
    }
    return mk?ans:mod-ans;
}
pr fa[205][205];
char ss[205];
int n,m;
int dy[205][205]; int tot;
bool vis[205][205],flag;
pr gf(int x,int y) {
    if(vis[x][y]) {
        flag = 1; return pr(0,0);
    }
    pr tmp;
    vis[x][y] = 1;
    if(fa[x][y]==pr(x,y) ) tmp = pr(x,y);
    else tmp = gf(fa[x][y].fi,fa[x][y].se);
    vis[x][y]=0;
    fa[x][y] = tmp;
    return tmp;
}
int X[305],Y[305];
void solve() {
    flag = 0;
    scanf("%d%d",&n,&m);
    tot = 0;
    fa[0][0] = pr(0,0); dy[0][0] = ++tot;
    for(int i=1;i<=n;i++) {
        scanf("%s",&ss[1]);
        for(int j=1;j<=m;j++) {
            if(ss[j]=='.') dy[i][j] = ++tot,fa[i][j] = pr(i,j),X[tot]=i,Y[tot]=j;
            if(ss[j]=='U') fa[i][j] = (i==1?pr(0,0):pr(i-1,j));
            if(ss[j]=='D') fa[i][j] = (i==n?pr(0,0):pr(i+1,j));
            if(ss[j]=='L') fa[i][j] = (j==1?pr(0,0):pr(i,j-1));
            if(ss[j]=='R') fa[i][j] = (j==m?pr(0,0):pr(i,j+1));
        }
    }
    for(int i=1;i<=n;i++) {
        for(int j=1;j<=m;j++){
            gf(i,j);
            if(flag==1) {
                puts("0"); return;
            }
        }
    }
    for(int i=1;i<=tot;i++) {
        for(int j=1;j<=tot;j++) a[i][j]=0;
    }
    for(int i=2;i<=tot;i++) {
        int x = X[i]; int y = Y[i],t; pr oo;
        oo = x!=1?gf(x-1,y):pr(0,0);
        t = dy[oo.fi][oo.se];//t-->i
        if(t!=i)
            a[t][i] = add(a[t][i],mod-1),a[i][i]++;
        
        oo = x!=n?gf(x+1,y):pr(0,0);
        t = dy[oo.fi][oo.se];//t-->i
        if(t!=i)
            a[t][i] = add(a[t][i],mod-1),a[i][i]++;
        
        oo = y!=1?gf(x,y-1):pr(0,0);
        t = dy[oo.fi][oo.se];//t-->i
        if(t!=i)
            a[t][i] = add(a[t][i],mod-1),a[i][i]++;
        
        oo = y!=m?gf(x,y+1):pr(0,0);
        t = dy[oo.fi][oo.se];//t-->i
        if(t!=i)
            a[t][i] = add(a[t][i],mod-1),a[i][i]++;
        
    }
    printf("%d\n",gauss(tot));
}
int main() {
    int T;
    scanf("%d",&T);
    while(T--) solve();
}