浅谈二分
- 大家一定对二分法有所耳闻吧！它的定义是什么？它的用途又是什么？下面我就来介绍一下二分法及其用途。
引子
例题
找出函数\(f(x) = 3x - 3\)在闭区间\([0，4]\)的零点。
解法
- 首先，令\(L = -1\)，\(R = 1\)。
- 然后进行如下操作，直到\(f(mid) = 0\)为止。
- 算出\(L\)和\(R\)的代数平均数\(mid\)，且\(mid \in \mathbb{Z}\)，即整数\(mid = \lfloor \dfrac{a + b}{2} \rfloor\)。
-
- 若\(f(mid) = 0\)，找到答案
- 若\(f(mid) > 0\)，让\(b = mid\)，缩小区间
- 若\(f(mid) < 0\)，让\(a = mid\)，缩小区间
- 回到步骤\(1\)。
如果你没有明白的话，那就看图吧。。。
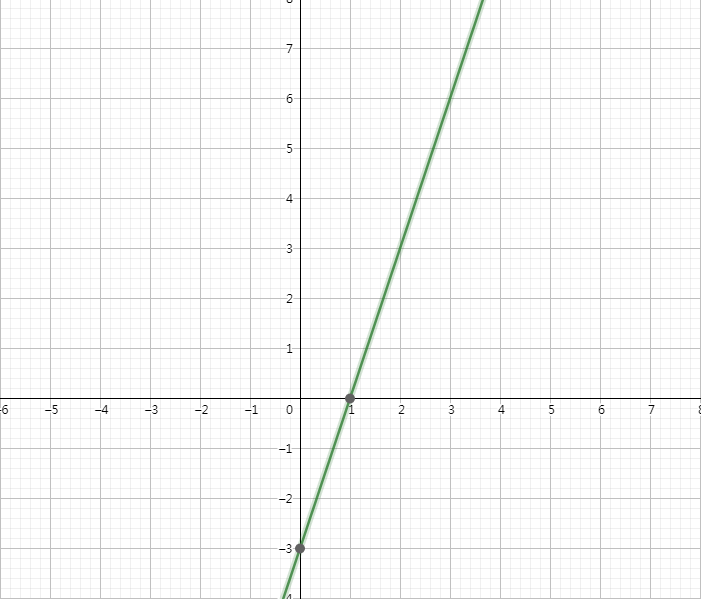
- \(L = 0, R = 4, mid = \lfloor \dfrac{0 + 4}{2} \rfloor = 2\)
- \(f(mid) = f(2) = 3 > 0\)
- 因为\(f(x)\)为单调递增函数，所以零点肯定在\(2\)左边。
- 缩小范围至\([0,2]\)，\(R = 2\)。
- 此时\(mid = \lfloor \dfrac{0 + 2}{2} \rfloor= 1\)
- \(f(mid) = f(1) = 0\)！
- 找到答案\(0\)。
例题回顾（条件）
- 在上面的例题中，能够正确地使用以上“缩小范围区间”的解法的条件是什么呢?
- 显然，函数\(f(x)\)需要是单调的，而到底是递增还是递减就无所谓了。
二分法
- 对于区间\([a, b]\)上连续不断且\(f(a) \times f(b) < 0\)的函数\(y=f(x)\)，通过不断地把函数\(f(x)\)的零点所在的区间一分为二，使区间的两个端点逐步逼近零点，进而得到零点近似值的方法叫二分法。
在信息学中，二分法最常见的体现就是二分答案。
在这篇随笔中，我主要讲解的就是二分答案。
二分答案
- 二分答案,是通过不断缩小解可能存在的范围,从而求得问题答案的方法。
举例
猜数字
-
事先准备一个\([1, 100]\)的正整数，让电脑猜。每次猜测会告诉猜数与答案的大小关系。
-
朴素的方法：枚举法，从\(1 - 100\)依次尝试，直到猜对为止。时间复杂度为\(O(n)\)。
-
二分答案：
\(L = 1, R = 100, mid = \lfloor \dfrac{L + R}{2} \rfloor = 50\)，设答案为\(ans\)。
只要\(L \leqslant R\)，尝试\(mid\)，\[ \left\{ \begin{aligned} & 若mid > ans，则R = mid； \\ & 若mid < ans，则L = mid + 1； \\ & 若mid = ans，猜对了。 \end{aligned} \right.\]时间复杂度为\(O(log n)\)。
为什么二分
- 更充分地利用已知条件，大幅度减少遍历范围
- 二分答案具有“先猜后证”的特点，可以给题目多增加一个条件，也许可以大幅度减小算法的时间开销
在什么情况下可以二分
- 答案存在单调性
什么意思呢？
我们不妨假设答案满足条件为\(1\)，不满足为\(0\)；
那么如果一个答案序列为\(0000000111\)或\(1111100000\)，都存在单调性，那就都可以；
而如果序列是\(000011011000110000\)，那就不满足单调性，于是就不能进行二分答案了。
能够解决的问题
二分答案能够解决哪些问题呢？如下：
- 最大的最小值
- 最小的最大值
- 在满足条件的情况下的最小（大）值
- 最接近一个值的值
- …… 在一个单调序列中特殊的点基本上都能二分。
模板（\(C++\)）
// 这是一个求满足条件的最小值的二分模板
int left = 0, right = MAX, mid, ans; // left为左边界，right为右边界
while(left <= right){ // 只要存在区间
mid = (left + right) >> 1; // 等价于(left + right) / 2，只不过这样写运行速度会稍快一些
if(check(mid)) ans = mid, right = mid - 1; // 如果mid满足条件，那ans（答案）肯定不大于mid
else left = mid + 1; // 如果不能满足条件，ans区间最小值肯定大于mid
} printf("%d\n", ans); // 输出答案
为什么第五行要加上ans = mid呢？
原因：如果\(mid\)恰好就是正确答案，\(check(mid)\)满足，为\(true\)，于是进入本句。如果将\(right\)设为\(mid - 1\)的话，就永远得不到\(ans\)了（可以想一想为什么）
这就出现了另一种写法——
// 这是一个求满足条件的最小值的二分模板
int left = 0, right = MAX, mid; // left为左边界，right为右边界
while(left < right){ // #注意这里改变#
mid = (left + right) >> 1; // 等价于(left + right) / 2，只不过这样写运行速度会稍快一些
if(check(mid)) right = mid; // #注意这里也改变#
else left = mid + 1; // 如果不能满足条件，ans区间最小值肯定大于mid
} printf("%d\n", right); // 输出答案
不过我个人建议还是写第一种好（更好理解，不容易错）。
那这两段代码中的\(check\)函数是干什么的呢？
其实，布尔型函数\(check(x)\)是用来判断\(x\)条件下是否能成功（满足题目条件）。
练习题
-
营救 （如果不会最小生成树请自动跳过~）
-
……
