动态规划——所有点对最短路径问题

所有点对的最短路径问题

​ 按照书上所说，\(d^k_{i,j}\)代表了点\(i\) 到 \(j\) 经过 \(1 or 2 or 3 or 4 ...... k\)的最短路径长度，比如\(d^3_{1,6}\)表示点1到点6， 可以经过点1，点2，点3的最短长度。

算法基本思路：

引理，点 i 到点 j 的最短路径可能是点 i 到点 j 的直接路径长度，也可能是以某点 k 为中间节点，i, k, j 的路径长度。

采用自底向上逐步求解的方法，设\(D_{i,j}^k\)表示 点 i 到 j 以点集[0..k] 为中间节点的最短路径。

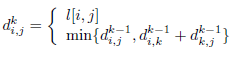
k 从0开始枚举各点，则第一步先求所有点以可能经过点0为中间节点的最短路径；

第二步求所有点以可能经过点1为中间节点的最短路径，在此时所有的D[i, j] 已经考虑过0作为中间节点的最短路径，即第二步做的是以点集[0..1]作为考虑，满足自底向上，不难看出，到了最后一步，就是以点集[0...n-1]作为考虑，此时求得的D[i, j] 就是最短路径。

如：

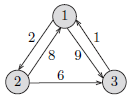
初始： k = 0

\[\begin{bmatrix} 0& 2 &9 \\ 8& 0& 6\\ 1& ∞& 6\\ \end{bmatrix} \]

先代入公式 k = 0时，有 \(D_0[i,j] = L[i, j]\); 所以有 \(D_0 = \begin{bmatrix} 0& 2 &9 \\ 8& 0& 6\\ 1& ∞& 0\\ \end{bmatrix}\)

之后计算D1, 按照公式有 \(D_1 = min(D_0[i,j],D_0[i,k] + D_0[k,j]) \\所以 D_1= \begin{bmatrix} 0& 2 &9 \\ 8& 0& 6\\ 1& 3& 0\\ \end{bmatrix}\)

以此类推，当计算到\(D_3\)时，说明已经是经过整个点集的最短路径

以下是python代码实现：

n = 3                                  //n*n的矩阵
D = [                           
    [0, 2, 9],
    [8, 0, 6],
    [1, 9999999, 6]
]
for k in range(0, 3):                    //从D_0到D_k进行k次运算
    for i in range(0, 3):                //i从0到3
        for j in range(0, 3):			//j从0到3，给每条边赋值
            D[i][j] = min(D[i][j], D[i][k] + D[k][j])
print(D)                         //打印矩阵