21/6/29 读书笔记 数据汇总统计与可视化 GMW协议 Shamir秘密共享方案 BGW协议
21/6/29 读书笔记
安全多方计算 Goldreich-Micali-Wigderson(GMW)协议
GMW协议中与GC的理念区别在于,对于每个wire,GC中P1扮演了主要的角色,其需要采用\(OT_1^2\)传输来向P2传递密文,而P2则相对被动。而在GMW中,对wire的值进行了share,提高了P2的主动性。
GMW支持NOT、XOR和AND计算,其相比于GC的最大优势在于能拓展到更多方的共同计算。
对于一个gate,记为\(G\),其具有两个输入wire(\(x,y\))和一个输出wire(\(w\)),假设参与者P1和P2分别持有\(x\)和\(y\),考虑\(x,y,w\)∈{0,1}:
-
P1随机生成一个bit,称之为\(x_a\),\(x_b=x \bigoplus x_a\),在这里我们可以称\(\{x_a,x_b\}\)构成了x的一组share,\(x_a\)视为x的mask。将\(x_b\)发送给P2
-
P2同样对其持有的\(y\)生成一组share记为{\(y_a,y_b\)},并将\(y_b\)发送给P1。
-
讨论\(G\)的逻辑运算类型:
-
非运算 NOT(假设对x进行):则P1直接翻转就行,无需通信
-
异或运算 XOR:P1和P2分别对自己持有的{\(x_a,y_b\)}、{\(x_b,y_a\)}进行计算,得出\(w_1=x_a\bigoplus y_b,w_2=x_b \bigoplus y_a\),然后P1和P2各自展示\(w_1\)和\(w_2\),由\(w=w_1\bigoplus w_2=x\bigoplus y\)得到输出
-
与运算 AND:较为复杂,需要使用\(OT_1^4\)。P1首先需要考量一个算式:
\[w=S(x_b,y_a)=(x_a\bigoplus x_b) \and (y_a\bigoplus y_b) \]这个算式与P2持有的{\(x_b,y_a\)}有关,P1需要去猜测其组合的所有可能性,即{\(x_b,y_a\)}属于{{0,0}, {0,1}, {1,0}, {1,1}}。P1在计算得到所有的四个结果后,还需要额外为自己生成一个计算密钥\(k\in\{0,1\}\),并将所有的结果通过\(k\bigoplus S\)进行加密,将加密的结果通过\(OT_1^4\)发送给P2。P2得到被加密的结果后,P1和P2分别公布\(k\)和被加密的结果,最后通过\(w=w\bigoplus k \bigoplus k\)得到最终结果
注意这里,即使P1明明知道\(x_b\),但是它仍然考虑了\(x_b\)的不同情况。在\(x_b\)对P1已知的情况下,也许可以采用\(OT_1^2\)替代\(OT_1^4\)?我没有想到为什么不这样做的理由。
-
而为了拓展到多方(n方参与)的场景,只需要将share的部分改为产生(n-1)个mask,然后将mask发送出去(注意,这里区别于上述的双方GMW过程)。但是实际上只是share的一个生成方法罢了,没啥区别。其他考量基本一致,不再赘述。
安全多方计算 Shamir秘密共享方案
Shamir秘密共享方案是基于多项式插值法构造的具有门限的n方秘密共享方案。n个人共享一个秘密s,而仅当t个人以上提供其具有的share,才能还原出秘密s。
其构造方式可以描述为:
-
对于秘密s,给定一个值p,构造一个多项式如下:
\[f(x)=(s+a_1x+a_2x^2+...+a_{t-1}x^{t-1})mod(p) \] -
给定n个随机值,每个随机值称为\(r_i\),求得\(f(r_i)\),然后将\((r_i,f(r_i))\)发送给第i个参与者。分发完成后,多项式被销毁,秘密s被隐藏
-
根据数学原理,当我们拥有t个参与者持有的\((r_i,f(r_i))\)时,就能够重建原t次多项式,并得到秘密s。重建方式使用多项式插值法:
\[f(x)=\sum_{i=1}^{t}\left(\prod_{1 \leq j \leq t, j \neq i}\left(x-r_{j}\right)\left(r_{i}-r_{j}\right)^{-1}\right) f\left(r_{i}\right)(\bmod p) \]而\(s=f(0)\)
安全多方计算 BGW协议
BGW协议是基于Shamir秘密共享方案的支持算术运算的多方MPC协议。其支持加法、数乘运算、乘法运算。
考察一个算术门\(G\),其具有输入a和b:
-
基于Shamir方案,生成两个多项式\(f(x)和g(x)\)用于保存秘密a和b。生成n个随机值然后按方案进行处理和分发(即每个参与者\(P_i\)接收到\((r_i,f(r_i),g(r_i))\)),之后销毁多项式
-
考虑\(G\)的类型:
-
加法运算:每个参与者\(P_i\)计算自己的\(f(r_i)+g(r_i)\),而这个值就是最终\(a+b\)的一个share,仍然满足Shamir共享方案对门限t和n的要求
-
数乘运算(假设对a):每个参与者计算\(const * f(r_i)\),由于是线性的,仍然满足Shamir共享方案。
-
乘法运算:对于乘法运算,由于多项式相乘后,其次数会发生改变(从t次变为2t次),因此会打破Shamir共享方案。
我们需要采用拉格朗日插值方法对这个2t次的多项式进行分析,我们有n个\((r_i,f(r_i)*g(r_i))\),构成了n个点。基于这n个点进行插值(为了方便,设\(m_i=f(r_i)*g(r_i)\)):
\[a*b=\sum_{i=1}^{2t+1}\lambda_im_i \]其中\(\lambda_i\)是第i个点对应的拉格朗日系数(这个系数可以由所有的n个\(m_i\)和\(r_i\)共同计算出来)。
-
此时对于参与者\(P_i\),其持有\(m_i=f(r_i)*g(r_i)\)是一个已知数,其将这个\(m_i\)作为秘密,重新基于Shamir方案构造一个新的t次多项式\(t_i(x)\),并将秘密\(m_i\)以\((r_j^i,t_i(r_j^i))\)分发给参与者\(P_j(j\in (0,n])\)
-
现在每个参与者持有:
- 关于最终结果的一个share,即\(m_i\)
- 关于每一个参与者的\(m_i\)的share
他们可以共同计算出上面的式子(计算过程通过数乘和加法就能完成,因为\(m_i\)的发布是通过t次多项式完成的)
-
最终所有参与者公布结果的share,从而通过Shamir方案得到最终结果。由于参与拉格朗日多项式计算的公式都是我们重新构造的t次多项式,所以保持了门限为t
-
-
对于BGW方法,门限t必须满足\(2t<n\),否则在使用拉格朗日插值法时会发现没有足够的点进行插值(最多只能提供n个点,而2t级多项式的拉格朗日插值法需要2t个点)。
拉格朗日插值法:对于n次多项式\(h(x)\),假设知道n个满足该多项式的点\(\{(x_i,y_i)|i\in (0,n]\}\),可以通过:
\[B_k=\{j|i!=j 且 j\in (0,n]\}\\ e_k(x)=\prod_{i\in B_k}\frac{x-x_i}{x_k-x_i}\\ h(x)=\sum_{j=0}^{n-1}e_j(x)y_i \]上述BGW求取过程中特定于求取\(x=0\)的情况,即\(\lambda_i=e_i(0)\)
数据分析导论 数据探索 汇总统计
数据探索是对于数据的初步探索,以更好掌握其性质。将从汇总统计、可视化、联机分析处理三个主题进行介绍。
汇总统计是采用量化的数的集合来捕获和描述一个大的数据集合的某种特征。可以从以下角度进行统计分析:
-
频率和众数:众数对应较高频率的数据。对于离散的分类属性来说,其频率和众数具有较高的研究价值。对于连续的属性来说,众数通常会给出关于遗漏值的信息(比如指定0作为缺省值,就会使得0成为众数)
-
百分位数:给定一个\(x_{p\%}\),使得整个数据中百分之\(p\)的观测值小于\(x_{p\%}\)。百分位数是一些其他统计量的基础。
-
均值和中位数。均值和中位数给出了值集的位置度量。均值对离群值较为敏感,中位数则更稳健地提供了值集中间位置的估计。
- 截断均值:指定\(p\),将数据中前\(p\%\)和后\(p\%\)的数据剔除后,再求其他数据的均值。均值可以看做\(p=0\)的情况,中位数可以看做\(p=50\)的情况。
-
极差和方差:极值和方差给出了值集的散布度量。极差在大部分值相对集中、小部分值极端的情况下容易引发误解。标准差是方差的平方根,方差被描述为:
\[variance(x)=s_x^2=\frac{1}{m-1}\sum_{i=1}^m(x_i-\overline x) \]但是均值本身容易被极端值带偏,所以从方差引申出几个其他度量:
- 绝对平均偏差(absolute average deviation,AAD)
- 中位数绝对偏差(median absolute deviation,MAD)
- 四分位数极差(interquartile range,IQR)
\[AAD(x)=\frac 1m\sum_{i=1}^m\mid {x_i-\overline x}\mid\\ MAD(x)=median(\{\mid{x_1-\overline x,...,x_m-\overline x}\mid\})\\ IQR(x)=x_{75\%}-x_{25\%} \] -
多元汇总统计:当多个属性间具有一定关联关系,使得每个属性的散布不一定相对独立,这时使用协方差矩阵分析数据的散布。协方差矩阵\(S\)为\(m\times m\)的方阵,\(s_{ij}\)表示第i个属性和第j个属性的协方差:
\[covariance(x_i,x_j)=\frac1{m-1}\sum_{k=1}^m(x_{ki}-\overline{x_i})(x_{ki}-\overline{x_i}) \]可以看出协方差在i==j时表现为方差。协方差体现了多个属性一起变化的情况,协方差大小还依赖于变量的值域大小。协方差接近于0,表示两个属性间线性相关程度低。
而实际上更好的判断相关性的方式是(皮尔森)相关性矩阵,即每个元素都是相关属性间的皮尔森相关性度量(见数据相似性和相异性一节),其更好地排除了变量本身值域对于判断和对比的干扰。
数据挖掘导论 数据探索 可视化
可视化的理论基础在于相信人的分析能力和领域知识,而致力于如何采用可视化的方式将信息呈现给人,使得人能够从中快速发现和聚焦于某些模式。
可视化的重要概念在于:
- 表示:如何将数据的信息对应到图形中的元素。
- 安排:数据的安排需要合理,可视化图形的安排需要尽可能清晰,凸显出潜在的模式。
- 选择:对于多维的数据,如何选择能够体现所需关系的属性组合;以及在对象过多导致表示复杂时选择并删去微不足道的对象。
可视化的具体技术依赖于数据类型。
对于少量属性(低维非时序非空间序简单属性),可以用茎叶图、直方图等,熟悉的概念就不多介绍。以下介绍几种(我没见过的)表示技术:
- 盒状图:利用盒的特殊位置标识不同的百分位点,利用离散点表示异常值。其能够更在较为紧凑的情况下反映该属性的位置度量的同时,较为大概地反映散布度量。
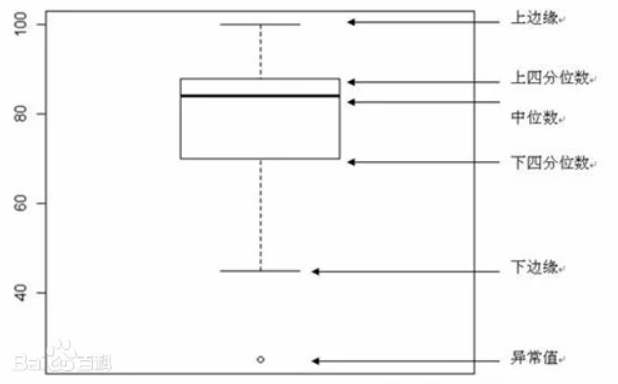
- 百分位图:横坐标为属性值x,纵坐标表示所有数据中小于等于x的对象所占的百分比,构成的函数称为(经验)累计分布函数((E)CDF)。你还可以构建其反函数来画图。其展现了在数据层面属性变化的趋势。
对于具有时序和空间序的数据,其常常在时间和空间上具有平滑连续性。因此对于这种数据的可视化可以用更加直观的曲面图、等高线图进行处理。而当需要同时考虑时间和空间维度时,对其中一个维度进行低维切片,即选取该连续维度空间内的离散点,针对该点固定,考察其他属性。
对于更高维数据,介绍了这几种方法:
-
数据矩阵图:利用颜色表示数值,每个不同的属性构成列,每个对象构成行,每个元素表示一个对象的一个属性。看起来和表差不多,只是使用图形元素替代了数值。
-
平行坐标系:纵坐标代表属性的值域,横坐标上每隔一定区间设置一个竖直轴,每个轴对应一个属性。每个对象的属性的值表现为这些轴上的点,连起这些点的一条折线代表一个对象。相似的对象之间的折线模式相似。对于属性轴的合理安排会提高图的清晰性。
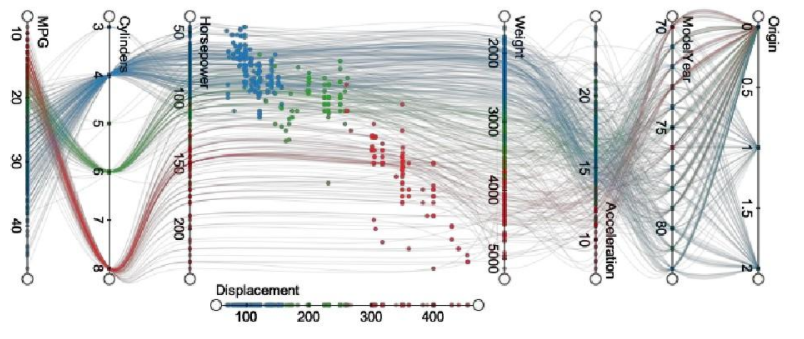
- 星型坐标系:每个对象都是一个替身,对应一个JOJO的替身面板,不用解释了吧(x
数据可视化的经验总结出以下的指南性原则——ACCENT原则:
- Apprehension 理解:最大化对变量间关系的理解
- Clarity 清晰:最重要的元素和关系在视觉上最突出
- Consistency 一致:多张可视化图之间对同一对象的表示要一致
- Efficiency 有效:尽可能简单和容易解释
- Necessity 必要:所有图形元素应该是必要的
- Truthfulness 真实:能够从图形元素获取到真实情况的隐性描述


 浙公网安备 33010602011771号
浙公网安备 33010602011771号