代码随想录——动态规划9不同的二叉搜索树

解题思路

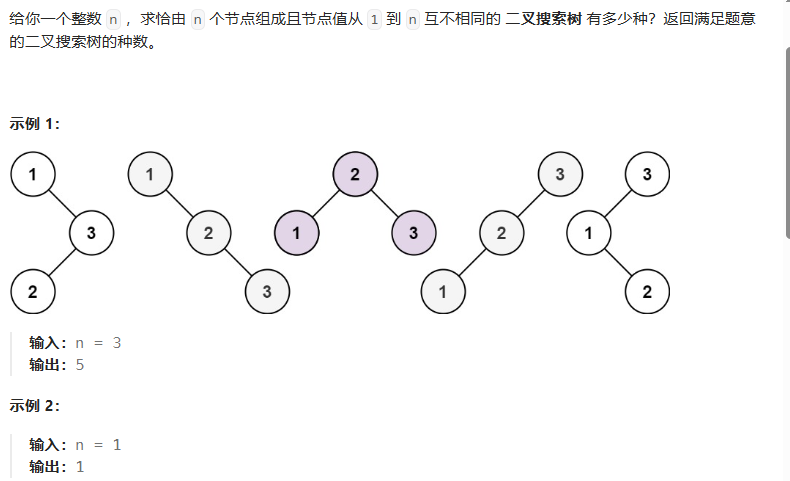
本题通过递归 和 二叉搜索树特性解决。

当n=1时，结果是1。如果n>1时，因为根节点值不同对应的二叉搜索树肯定不同，所以我们考虑根为i(2≤i≤n)的情况。
由二叉搜索树特性，根左边一定有i-1个元素，右边一定有n-i个元素。
设f(i)函数返回i个不同元素节点组成的二叉搜索树的个数。所以可得方程：

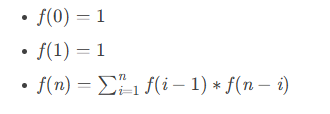
为减少递归调用带来的开销，用记忆化搜索的方式优化（动态规划的一种）。设dp数组而非f(i)函数。

代码如下

class Solution {
public:
    int numTrees(int n) {
        vector<int> dp(n+1);//dp[i]是i个不同元素节点组成的二叉搜索树的个数
        dp[0] = 1;
        for(int i=1;i<=n;i++){
            for(int j=1;j<=i;j++){
                dp[i] += dp[j-1] * dp[i-j];
            }
        }
        return dp[n];
    }
};