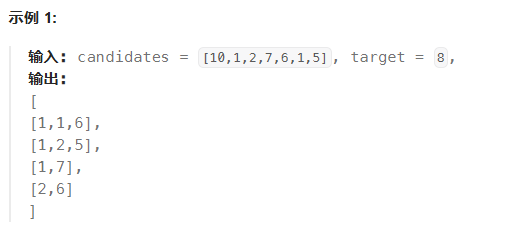
代码随想录——回溯8、组合总和II

这道题稍微有点难，我是突然想到要不试试把数组排序，画图发现只要出现candidates[i] == candidates[i-1]时（i>start)就可以剪枝，如下图

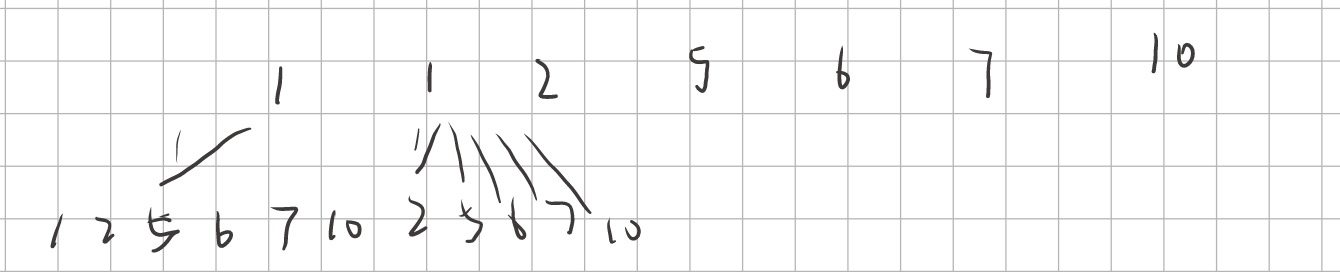
思路

首先这种去重的问题，用哈希表一般比较麻烦。可以从将数组先排序等变得好处理的角度去思考。

区别

这道题目和39.组合总和如下区别：

1. 本题candidates 中的每个数字在每个组合中只能使用一次。
2. 本题数组candidates的元素是有重复的，而39.组合总和是无重复元素的数组candidates
   最后本题和39.组合总和要求一样，解集不能包含重复的组合。

本题的难点在于区别2中：集合（数组candidates）有重复元素，但还不能有重复的组合。

分析

所谓去重，其实就是使用过的元素不能重复选取。组合问题可以抽象为树形结构，那么“使用过”在这个树形结构上是有两个维度的，一个维度是同一树枝上使用过，一个维度是同一树层上使用过。

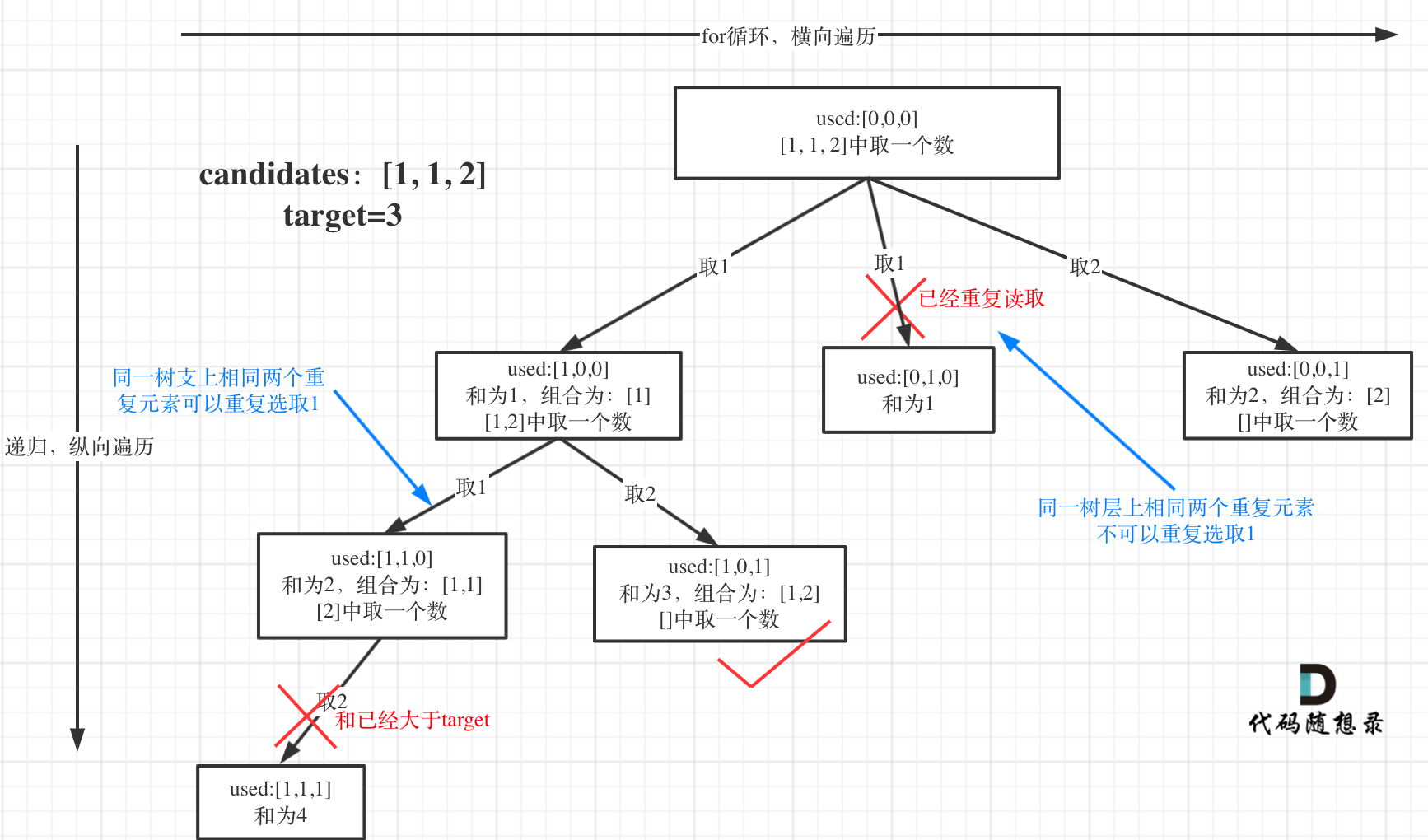
我们要去重的是同一树层上的“使用过”，同一树枝上的都是一个组合里的元素，不用去重。

而树层去重的话，需要对数组排序！

代码

标准回溯模板的基础上加上去重判断和排序。

class Solution {
public:
    vector<int> path;
    vector<vector<int>> result;
    void backTracking(vector<int>& candidates,int sum,int start){
        if(sum == 0){
            result.emplace_back(path);

            return;
        }else if(sum < 0)return;
        //核心：要去掉重复的组合
        int last=-1;
        for(int i=start;i<candidates.size();i++){
            if(candidates[i] == last)continue;
            last = candidates[i];
            path.emplace_back(candidates[i]);
            backTracking(candidates,sum-candidates[i],i+1);
            path.pop_back();
        }
    }

    vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
        sort(candidates.begin(),candidates.end());
        backTracking(candidates,target,0);
        return result;
    }
};