代码随想录——25.二叉搜索树中的众数

思路

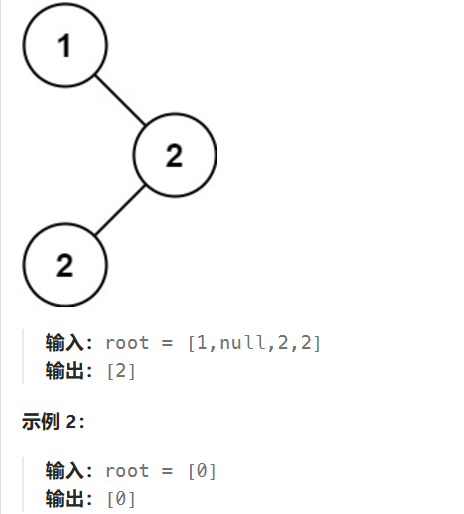
1. 利用二叉搜索树性质，先序遍历是递增序列
2. 加上进阶要求，问题转换为：对于一个递增序列，在时间复杂度O(N)，空间复杂度O(1)内找到所有的众数

由于是递增序列，因此众数一定是挨在一起的。遍历序列时判断前后两个数是否相同来增加该数出现次数。（初始化次数为1）
利用上一题的“记录前后两个节点”的操作，比较pre和cur的值。设curTimes和MaxTimes表示当前该数出现频次和最大出现频次。

代码

我了个骚杠，写的屎山代码还真的过了

class Solution {
public:
    vector<int> res;
    int maxTimes=INT_MIN;
    int curTimes;
    TreeNode* pre;
    void dfs(TreeNode* root){
        if(root == nullptr)return;
        dfs(root->left);//左
	//根
        if(pre!=nullptr){
            if(root->val == pre->val){
                curTimes++;
            }else{//不等时curTimes=1而不是0
                curTimes=1;
            }
	//重点：如果相等直接加入；当前频次更大说明之前的都不是众数，直接clear数组
            if(curTimes == maxTimes){
                res.emplace_back(root->val);
            }else if(curTimes > maxTimes)
                maxTimes = curTimes;
                res.clear();
                res.emplace_back(root->val);
            }
        }else if(pre == nullptr){//只有一个数特判一下
            curTimes = 1;
            maxTimes = 1;
            res.emplace_back(root->val);
        }
        pre = root;
	//右
        dfs(root->right);
    }
    vector<int> findMode(TreeNode* root) {
        //问题转换为：对于一个递增序列，在时间复杂度O(N)，空间复杂度O(1)内找到所有的众数
        dfs(root);
        return res;
    }
};