Leetcode 42.接雨水

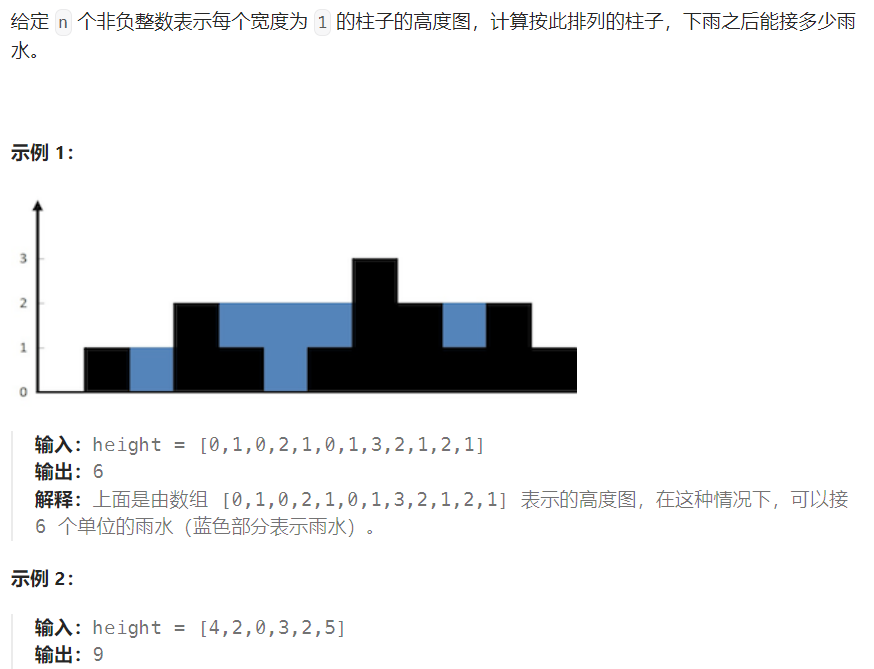
题目

朴素解法：

对于每列分别向左右扫描查找左右最高的柱子，对于每一个柱子接的水，那么它能接的水=min(左右两边最高柱子）-当前柱子高度。遍历每列时间复杂度为O(n)，每列再扫描O(n)，总共O(N^2)。

class Solution {
public:
    int trap(vector<int>& height) {
        //O(n^2)还是超时
        int ans=0;
        //按列求，只看每列能接多少水——找该列左右最高的柱子——短板效应
        for(int i=1;i<height.size();i++){
            int left = 0,right = 0;
            for(int j=0;j<i;j++)left = max(left,height[j]);
            for(int j=i+1;j<height.size();j++)right = max(right,height[j]);
            int temp = min(left,right);
            if(height[i] < temp)ans += temp-height[i];
        }
        return ans;
    }
};

动态规划：

每列都向左右扫描重复信息没有利用，考虑动态规划，用leftMax和rightMax数组记录每列的左右柱子最高高度。
在外部先两次for循环：

• 从左向右扫描得到leftMax：leftMax[i] = max(leftMax[i-1],height[i])
• 从右向左扫描得到rightMax：rightMax[i] = max(rightMax[i-1],height[i])
  此时内部不必for循环：

            for(int j=0;j<i;j++)left = max(left,height[j]);
            for(int j=i+1;j<height.size();j++)right = max(right,height[j]);

时间复杂度O(N),空间复杂度O(N)

双指针：

动态规划中维护两个数组占用O（N）的空间，我们能不能优化？

如果还是从左向右计算每列可接雨水而不提前扫描保存到rightMax数组，那么每次计算时不能知道右边柱子的最大高度（没扫描过）所以不妨改为一左一右的计算每列可接雨水。

维护两个指针 left 和 right，以及两个变量 leftMax 和 rightMax，
初始时 left=0,right=n−1,leftMax=0,rightMax=0。指针 left 只会向右移动，指针 right 只会向左移动，在移动指针的过程中维护两个变量 leftMax 和 rightMax 的值。

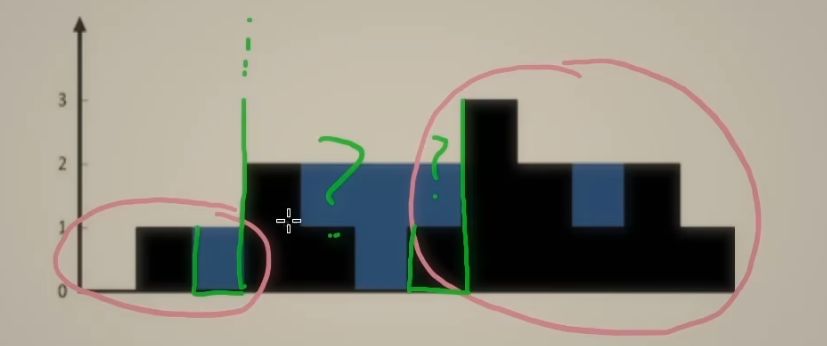
如图这种情况：

• 对于右边木桶，已知它右边最大高度是rightmax,但左边还不确定，所以不能计算水
• 对于左边木桶，已知它左边最大高度是leftmax,并且leftmax < rightmax，所以即使不知道它右边真正的最大高度是多少，这个木桶右边木板的最大高度至少就是rightmax了，它接的水只能是由短板leftmax决定了。

左边木桶算完了，左指针就可以向右移动了。

代码

class Solution {
public:
    int trap(vector<int>& height) {
        int ans=0,left = 0,right = height.size()-1,leftMax=0,rightMax=0;
        while(left < right){
            leftMax = max(leftMax,height[left]);
            rightMax = max(rightMax,height[right]);
            if(leftMax < rightMax){ // 左木桶的右木板至少是rightmax了，而左木板最大是leftmax。故接水量由leftmax决定
                ans += leftMax - height[left];
                left++;
            }else{
                ans += rightMax - height[right];
                right--;
            }
        }
        return ans;
    }

复杂度分析：

时间复杂度：O(n)，其中 n 是数组 的长度。两个指针的移动总次数不超过 n。

空间复杂度：O(1)。只需要使用常数的额外空间。