PRML读书后记(一): 拟合学习
高斯分布·拟合
1.1 优美的高斯分布
中心极限定理[P79]证明均匀分布和二项分布在数据量 $N\rightarrow \infty$ 时,都会演化近似为高斯分布。
作为最晚发现的概率分布,可以假设任何不确定的实数服从高斯分布。
对于回归问题,显然目标值 $t$ ,有 $t\sim N(\mu ,\sigma ^{2})$ 。
$t$ 服从的高斯分布表达形式很特殊,很有趣,也很奇妙:
$p(t|x,w,\beta)=N(t|y(x,w),\beta ^{-1})$ [P140]
即分布的均值(期望)为参数拟合值,方差为 $\beta ^{-1}$。
撇开概率不谈,拟合值 $y(x,w)$ 和 目标值 $t$ 之间通常是有误差的,来源应该有二:
I、拟合精度问题,给定一个指定函数,若通过迭代法近似,显然梯度下降为指定函数的参数几乎是不可能的。
这里不考虑线性回归参数可以用极大似然算出来,扩展到一个非常复杂的神经网络目标函数。
II、数据质量不佳,比如目标值 $t^{'}$ 被人为标记错了,和正确的值 $t$ 有偏差。
这时候,就算是100%完美拟合,最多有$ y(x,w)=t' $,显然 $t' \neq t$
那么就假设误差为 $\epsilon$ , 统一定义 $t$ 的形式:
$t=y(x,w)+\epsilon \quad where \quad \epsilon \sim N(0,\beta ^{-1})$
假设误差$\epsilon$服从一个零均值的高斯分布,并且结合 $t$ 的统一形式,将这个高斯分布嵌入 $t$ 的高斯分布。
[P29]图1.16很好的描绘了这样表达的优美之处:

即按照高斯分布的$3\sigma$规则,真实的目标值由 $t$ 在最佳拟合值 $y(x,w)$ 附近偏移得到。
1.2 极大似然估计的病态拟合
扩展到有N条的数据集 $(X,T)$ 中,通常假设各条数据之间是独立的,根据[P17]的独立性Product Rule:
$P(X,Y)=P(X)P(Y)$
则多数据点 $T$ 的高斯分布: $P(T|X,w,\beta )=\prod _{i=1}^{N}N(t_{n}|w^{T}\phi (x_{n}),\beta ^{-1})$
取对数之后,有:
$ln \, p(T|X,w,\beta )=\frac{N}{2}ln\beta -\frac{N}{2}ln(2\pi)-\beta E_{D}(w) \quad where \quad E_{D}(w)=\frac{1}{2}\sum_{i=1}^{N}\{\,t_{n}-w^{T}\phi (x_{n})\,\}^{2}$
$\beta E_{D}(w)$ 中的$\beta$没有任何意义的,可以被约去,形成LMS的目标函数$E_{D}(w)$,数学解释是假设目标值t服从高斯分布。
在对数似然函数上做极大似然估计,若模型是简单的线性回归,则 $W_{ML}$ 可以无须通过迭代法而较为精确的算出:
$W_{ML}=(\Phi^{T} \Phi )^{-1}\Phi^{T}T$
这是一个代价昂贵且不是万能的计算:
I、$(\Phi^{T} \Phi )$的逆矩阵不一定存在
II、求逆矩阵的时间复杂度达$O(n^3)$
而且很容易被误导,只要$\Phi$在宣传报道上出现了偏差,那么$W_{ML}$是要负责的,变成对 $\Phi$ 的膜拜性过拟合。
而对于复杂的神经网络而言,无法推导也无必要推导$W_{ML}$的准确形式,只需使用普适的迭代近似方法求解。
参数·Regularizer
极大似然估计是个好方法,但直接对$P(t|w)$做极大似然估计却是糟糕透顶。
对$P(t|w)$做极大似然估计无外乎两个步骤:先算$P(t|w,\beta)$,再近似$P(w)$。
这不是一个好主意,因为$P(w)$看起来是$P(t|w,\beta)$算出的附带品,没有主动权。
若要取得主动权,就必须对$P(w|t)$做极大似然估计,根据贝叶斯条件概率分析相关变量:
$P(w|t)=\frac{ P(t|w)P(w)}{P(t)}$
在优化过程中,分子这样的归一化因子可以忽视,它的作用只是为了将概率归一化到[0,1]范围。
按照[P30]的写法最能表现出贝叶斯方法的意境,似然分布与参数先验分布构成共轭双生子形式:
$P(w|t)_{[Posterior]}\propto P(t|w)\,_{[Likelihood]} \cdot P(w)\,_{[Prior]}$
按照此方法,经过后验强化的参数W受到两部分影响:
I、观测数据本身,由似然函数$P(t|w)\,_{[Likelihood]}$
II、先验知识约束,由注入的$P(w)\,_{[Prior]}$
由于引入先验知识来干涉W的优化方向,此时做的极大似然估计蜕变为最大后验估计(MAP)。
2.1 先验知识:高斯分布
高斯分布应该算是我们认知中,描绘一切连续型数值不确定性的最基本、最硬派的先验知识了。
甭管你是什么妖魔鬼怪,只要你是连续的,不是离散的,先给你套个高斯分布的罪状。
当然,钦定高斯分布从数学角度是由原因的,和其优美的数学共轭形式有关。
[P98]的练习证明了,高斯似然分布 x 高斯先验分布,结果仍然是一个高斯分布。
(此证明需要熟读第二章关于高斯分布的 150 个公式,需要很好的概率论、线代基础。)
高斯分布在数学形式上有许多便利,比如下面提到的零均值简化版高斯分布,这为贝叶斯方法招来很多
恶评,[P23] 是这样解释的:贝叶斯方法广受批判的原因之一,是因为其在选取先验概率分布上,根据的是
数学形式的便利为基础而不是 先验分布的信度 。
贝叶斯方法讲究推导严谨,公式齐全,对于那些奇怪的、无法用数学语言表达原理的、广布自然界的先验知识,
如Deep Learning思想,自然不会考虑,这也是为什么有人会认为Deep Learning与Bayesian是对着干的。[Quora]
2.1.1 波动性惩罚:简化高斯分布
描述服从多元高斯分布的W的基本式如下:
$P(w)=N(w|m_{0},S_{0})$ [P152]
$m_{0}$ 为均值向量,$S_{0}$ 为协方差矩阵,下标为0表明这是注入的先验信息,无法修改。
在获得N个观测数据后,多元后验高斯分布的基本式如下:
$P(w|T)=N(w|m_{N},S_{N})$ [P153]
若W的先验分布设置为一般的多元高斯分布,那么$m_{N}$、$S_{N}$的形式会很复杂。
考虑设置一个特殊的先验高斯分布,它很Simple:
$N(w|0,\alpha^{-1}I)$
这个高斯分布有两个特殊之处:
I、均值向量为0,这样就把W分布的中心定位在原点。
II、协方差矩阵,除了对角线外,全部为0。对角线上,统一由单值$\alpha^{-1}$掌管。
尽管I、II的做法都是从数学形式角度考虑的简化,但是II中对协方差矩阵的处理带来了一个意外收获。
首先复习一下关于协方差矩阵的特性,它有两个关键点:
I、非对角线元素$A_{i,j}$,表明不确定元$i$、$j$之间的协方差,即$cov(i,j)$
与协方差联系最多的就是相关系数,$\rho_{i,j}$
$\rho_{i,j}=0$表明不确定元$i$、$j$不存在线性相关,但仍然保留着线性不相关,这种简化无伤大雅。
II、对角线元素$A_{i,i}$,正是不确定元$i$自己本身的方差。
如果$\alpha$很大,即$\alpha^{-1}$很小,那么不确定元$i$无形之中受到了一种 惩罚 。
这种惩罚是从方差上的压制,方差被压制为小值,意味着不确定元$i$的波动性锐减。
波动性意味着什么?参数W的对数据的拟合的敏感性(Sensitive)。这种简化无形之中形成了这种惩罚。
简化高斯分布在取负似然对数之后,呈现更加优美的数学形式:
$-ln\,p(w|T)= \frac{\beta}{2}\sum _{n=1}^{N}\{t_{n}-w^{T}\phi (x_{n})\}^{2}+\frac{\alpha}{2}W^{T}W+const$ [P153式+取负对数似然]
在优化最小值时,第一部分在尽力使误差最小化,第二部分则在尽力惩罚参数——使$W^{T}W$最小化,无限朝0逼近。
第二部分在Regularizer机制中称为:L2 Regularizer,它的作用是减轻由于参数空间过大造成的过拟合(维数灾难型过拟合)
既可以从高斯分布理解:对拟合不敏感了,不行了,衰了。
也可以从$W^{T}W$最小化、维数灾难理解:尽管维数保留着,但是各维度的总轴长被控制的很小。
考虑一个幂函数$x^{D}$,尽管$D$很大, 但是基$x$并不大,最后的函数值也就不会膨胀得很大。
2.1.2 稀疏性惩罚:L1 Regularizer
简化高斯共轭分布,意外地为参数W带来一种惩罚活跃度的方法,在负对数似然函数上,即附加部分的$\frac{\beta }{2}W^{T}W$。
以参数W的指数形式作为Regularizer的,指数型Regularizer函数可以归纳为:
$Regularizer(W,Q,\beta )=\frac{\beta }{2}\sum _{i=1}^{M}\left | w_{i} \right |^{Q}$
其中,$\beta$为系数,决定着Regularizer的强度。$Q$为指数,决定着Regularizer的表达形式。
当$Q=1$,变成了另一个重要的Regularizer——L1 Regularizer,它使$|W|$最小化,让W呈现稀疏0值。
稀疏性在Deep Learning中是很重要的思想,[Glorot11]中对于稀疏性,有几个比较有趣的观点:
I、大脑中有1000亿以上的神经元,但是同时只有1%~4%激活,而且每次激活的区域都不一样。
这是生物神经中的稀疏性。
II、稀疏性将原本信息缠绕密集数据给稀疏化,得到稀疏特征表达。比如将实数5,稀疏为一个[1,0,1]向量,
很容易线性可分了。又比如识别一直鸟,只要把噪声给稀疏掉,保留关键部位,最后就有更好的特征表达。
这是特征表达上的稀疏性,实际应用有[稀疏编码][深度神经网络],当然还有我们的生物神经网络。
当然,以上和L1 Regularizer毫无关系,因为它稀疏的姿势错了,要不然还要Deep Learning作甚。
首先,这个稀疏策略没有Adaptive性,它并不会智能地的发现哪里需要稀疏,哪里不需要稀疏。
从数学规划问题角度理解,它就是一个多元的约束条件,至于哪个元倒霉到被约束至0,这个没人能确定。
其次,参数W直接影响着模型拟合能力,对它错误地稀疏0化,会造成严重的欠拟合。
基于以上两点,不能认为L1与L2类似,就认为L1也能缓解过拟合,实际上它更有可能造成欠拟合。
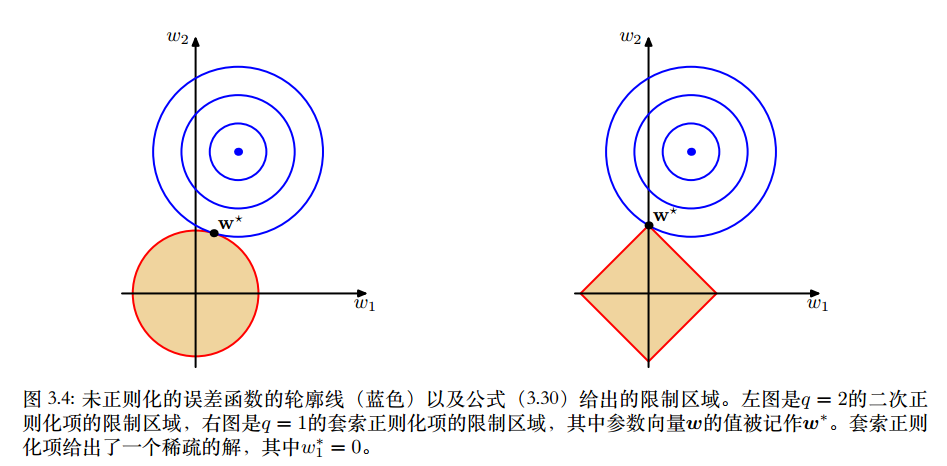
2.1.3 L1&L2 Regularizer 图形化理解
来自[P146]、[P107].CHS.HIT.马春鹏的有趣配图,似乎能解释为什么L1会直接得到0,而L2却是无限接近0。
2.1.4 更好地发现特征:Adaptive Represention Regularizer
Hinton组的[Erhan10] 认为Deep Learning的Pre-Training也是一个Regularizer,原因有二:
其一,预训练后参数W的搜索方向,有更大可能从局部最小值中逃逸。
其二,预训练后参数W的搜索方向,让似然函数值变大,但是得到了更好的归纳能力(测试错误率变低)。
第一点是比较神奇的Regularizer效果,即使是身披图灵奖的Bayesian方法,也是无法解释的。
第二点有点像是L2 Regularizer的效果,但是更大可能是与模型内部存有的Attention机制有关。
若是固定Pre-Training之后的参数W,那么Pre-Training等效于一个非线性的PCA,预先注入了
对无标签观测数据的先验知识,即得到了更合理的$P(W)$,这又是Bayesian方法所无法解释的。
2.1.5 可靠的稀疏性:Adaptive Sparsity Regularizer
Deep Learning中有两个能够自适应引入稀疏性的方法,[ReLU]&[Dropout]。
I、[ReLU]对神经元的输出稀疏,而神经元的输出显然是可变的。
II、[Dropout]是对神经元的输出稀疏,不过方式有点特别,采用随机概率来决定,而不是自适应方法。
但这并不能表明[Dropout]得不到自适应稀疏,它的自适应恰恰来自于随机本身。
由于随机性,每次网络结构都不同,这压迫了参数W朝一个稳定方向调整。
如2.1.2分析,[I]可以认为是发现了稀疏特征,替代L1。[II]可以认为是类似生物神经网络的稀疏激活机制,替代L2。
这两者并不冲突,所以常规Deep Learning模型中,[I]+[II]是标配手段。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号