神经网络模型算法与生物神经网络的最新联系
来源
偶然翻了一下微博,发现了@爱可可-爱生活老师转的,Hinton教授今年六月末在剑桥的一个讲座。

视频度娘链接:http://pan.baidu.com/s/1eQjj0rS
整个讲座前半部分基本在回顾DL目前的几个成就:RBM、DNN、CNN、RNN、Dropout
以及在CV、NLP、Speech方面的应用,这部分没什么可在意的。
有趣的是,Hinton在中间插了一段对自己(还有学界)的吐槽,大致就是1986~2006这20年间毫无作为的反思,
也是神经网络模型体系在这20年间犯的四大错误:
★Our labeled datasets were thousands of times too small.
分析:LeCun搞的MNIST在当时看起来,6W的数据量是客观的,结果神经网络(CNN)跑的没Hand-Made特征好,
大家就埋怨神经网络垃圾. 2009年ImageNet立项后,1500W的数据,千倍的强化,神经网络立刻甩开了SIFT
这类的Hand-Made特征,CV界老一辈气得半死。
★Our computers were millions of times too slow.
分析:早期是单机CPU单线程。Intel给力后,多线程算法开始流行,变成单机CPU多线程。
这几年云计算给力后,有变成云CPU多线程。后来NVIDIA发功了,现在又是云GPU多线程。
计算力上去百万倍,跑神经网络才毫无压力。
★We initializaed the weights in a stupid way.
分析:早期神经网络初始化,清一色的 $W\sim Uniform(-\frac{1}{\sqrt{LayerInput}},\frac{1}{\sqrt{LayerOut}})$
Bengio组的Xavier在2010年推出了一个更合适的范围,能够使得隐层Sigmoid系函数获得最好的激活范围。
对于Log-Sigmoid: $[-4*\frac{\sqrt{6}}{\sqrt{LayerInput+LayerOut}},4*\frac{\sqrt{6}}{\sqrt{LayerInput+LayerOut}}]$
对于Tanh-Sigmoid: $[\frac{\sqrt{6}}{\sqrt{LayerInput+LayerOut}},\frac{\sqrt{6}}{\sqrt{LayerInput+LayerOut}}]$
当然,这些仍然有些Stupid。Hinton指的“Smart”是指用Unsuprvised Learning学习出初始值,即Pre-Training。
★We used the wrong type of non-linearty.
分析: Simgoid函数祸害了几十年。虽然中间出现过RBF径向基函数,但因为找径向基中心麻烦,
RBF很快就被遗弃了。Sigmoid春风吹满地。直到2010年后,才普遍推广ReLU.
Hinton顺便解释了ReLU有效的原因,这点在其他paper倒是很少见到:
☻They automatically equalize the magnitude of gradient in different layers
-Layers with big weights get small gradients
-Layers with small weights get big gradients
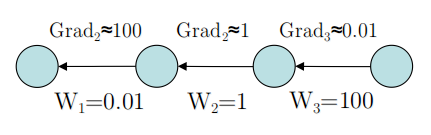
从图上来看,就是ReLU的非饱和性,使得Gradient在各层拥有弹性缩放能力。
至于为什么Layer越高,Weight越大,个人猜测是较高层较Sensitive,调整幅度较大。
毕竟0.01是默认Random值,Traning过程中变大也是可能的。
生物神经网络 VS 神经网络模型
讲座的后半部分比较高潮,Hinton充分展示了他在认知心理学、计算神经学、脑机制多方面的研究:
以生物神经学界向计算神经学界提出的四大否定结论发难。
这四点基本招招致命,分分钟都能推翻整个神经网络模型体系。
挑战书一:生物神经元不可能进行数值计算
★Cortical neurons do not communicate real-valued activities. (2012年)
-Current Solved: They send spikes.
分析:脑皮层神经元之间,可不会用实数值来交流。(数字体系是人类文明的高度抽象)
目前已经这个问题已经被解决,神经元之间发spikes来交流。
百度关键词:spike+神经,spike是神经学术语,指的是单神经元发的电信号。
电信号的频率、强度一定程度上可以模拟数字计算体系。
挑战书二:生物神经元难道会自动求导?
★How do neurons know $\frac{dy}{dx}$(Gradient)
分析:请发功,用神经元,秒解一个N元M次函数的求导问题。(想想也不可能)
挑战书三:生物神经元是否真的需要发两种信号(前向传播+反向传播)?
★The neurons need to send two different types of signal
-Forward Pass (Signal=activity=y)
-Backward Pass (Signal=$\frac{dE}{dx}$)
分析:生物神经元可以正向传播,但反向传播信号太复杂,生物神经元没有对应结构去传播。
挑战书四:生物神经网络元没有同值的互连接
★Neurons do not have point-wise reciprocal connections with the same weight in both directions.
分析:整个讲座最费解的地方。只提供个人见解。
一般而言,生物神经元没有输入、输出之分,输出神经元肯定连着输出神经元,在输出之后,电信号的下一跳就成了输入神经元。
两个神经元之间,通过对输出神经元的解码,输入神经元可以拿到输入信息。
而前馈网络,包括算法,完全就是代码上的硬跳转实现循环训练,这就使得新的输入还是上次的输入。
两个方向很有可能指的是:
I、输入--->输出
II、输出--->输入--->输出
我们的算法,很明显有 $I=II$ 。然而对于生物神经而言,很有可能 $I\neq II$。
Hinton的解释
很多东西都比较玄,只能说目前还能含糊过去。
解释一:符合泊松过程的电信号机制
要点:
★Synapses are much cheaper than training cases.
-We have 10^14 synapses and are for 10^9 seconds(3年)
分析:神经突触数量庞大,更新周期3年(疑问?),所以发电信号来计算很廉价.
★Sending random spikes from Possion process is very similar to dropout
-It is better than sending real-values.
分析:如此庞大数量的神经突触,肯定不会同时激活的。激活过程疑似泊松过程,
即每次随机抽出部分神经突触发电信号,这点和Dropout过程相近。
★A good way to throw a lot of parameters at a task is to use big neural networkswith dropout
分析:补上一个要点,大型模型相当于建立一堆突触,而Dropout每次只激活部分,屏蔽大部分参数。
解释二:Error误差导数的生物神经编码体系
生物神经学界的一个观点就是:生物神经元不可能完成复杂求导计算,然后反向传播。
Hinton给出了一个神奇的生物神经编码体系,
要点:
★Don’t compute it. Measure it.
Make a small change to the total input and observe the resulting small change in the total output.
分析:生物神经元不需要复杂计算,而是有一种通过简单的观测,来修正参数的方法.
★编码体系:
传统导数体系:
$\frac{dE}{dx}=Target-y$
基于时间的生物神经编码体系:
$\Delta Neuron(t)=y+t(Target-y) \quad where t=1,2,3.....Time$
Hinton把这个非求导的$\Delta$更新量称之为“时间导数",意思就是:
任意复杂函数的导数,都能由N个基于时间的线性函数构成。
不同时间段,以不同频率,放出不同强度的电信号,这些电信号足以模拟出任何函数的导数。
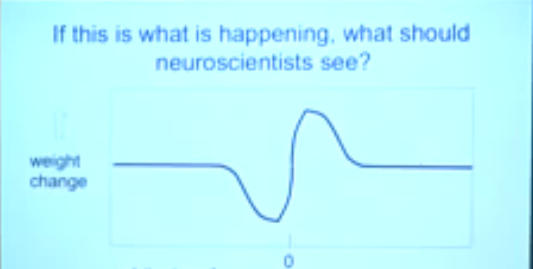
对于这个图,Hinton又补充了一句:
★Spike-time-dependent plasticity is just a derivative filter.
You need a computation theory (not a billion euros) to recognize what you discovered!
分析:神经元的发电形态相当于一个(时间)导数滤波器。
你得用复杂的计算理论(就是建立复杂的观测模型)来从神经元放电图像中获知信息。
值得注意的是 not a billion euros,应该并不是术语。
百度关键词 billion euro+神经 ,第一个结果就是欧盟12亿元模拟人脑计划:人类大脑工程
疑似Hinton在吐槽这个梗:砸数亿欧元,你也无法知道神经元的具体工作信息。
推测根据是,之前看到的对Yann LeCun的采访 http://www.huxiu.com/article/109035/1.html:
LeCun:从根本上说,欧盟人脑计划(Human Brain Project)中的很大部分也是基于这样一种理念:
我们应该建造一种模拟神经元功能的芯片,越接近越好,然后将芯片用于建造超级计算机,
当我们用一些学习规则来开启它时,人工智能就出现了。我认为这纯属胡说八道。
诚然,我刚才指的是欧盟人脑计划,并不是讽刺参与这个项目的每个人。
许多人参与该项目的原因仅仅是因为它能获得巨额资助,这是他们所无法拒绝的。
似乎整个北美学界都对欧盟的这个计划不满,Hinton在加入Google之前几乎是穷困潦倒了,而欧盟却在
这挥霍浪费,乱烧钱。
解释三:双向连接回炉机制


前馈网络存在的一个最大问题就是双向连接。即在模型中:输出神经元没有和输入神经元建立连接。
生物神经元不分彼此,从输出可以循环退回到输入,然后重复工作。
而目前神经网络模型的训练算法,则是以:
$While(Not Converged)$
$Forward-Pass$
$Backward-Pass$
程序的循环机制,本质是硬件上的硬跳跃,生物神经元可没有这么厉害的高级功能。
为了解决这个矛盾,Hinton以AutoEncoder做了一个假设:
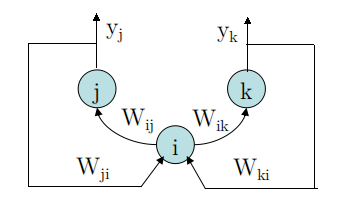
要点:
★If the AutoEncoder is perfect,replacing the bottom-up input by the top-down input,
will have no effect on the input of i.
If we then start moving $y_{j}$ and $y_{k}$ towards their target values,we get:
$\tilde{x_{i}}=w_{ji} \cdot y_{j}+w_{ki} \cdot y_{k}$
分析:这里Hinton做了一个假设,他假设AutoEncoder已经完美完成Pre-Training,
然后逆转一下传播方向,进行Reconstruction(重构),这样就有:
$x=\tilde{x}$
以重构的$\tilde{x}$ 进行正向传播,在反向传播阶段:
$\Delta Neuron = (w_{ji} \cdot y_{j}+w_{ki} \cdot y_{k})\frac{dy_{i}}{dx_{i}}=\frac{dE}{dx_{i}}$
这个式子想要表达: 反向逆回去的$\tilde{x}$是可以再度参战的。
这个式子的存在,表明生物神经元可能存在反向逆权值,通过这个逆权值,建立循环连接,而不是硬件式地直接跳回去。
而反向逆权值,恰好可以通过Pre-Training得到,从另一方面又佐证了Pre-Training机制在生物神经网络中是可能存在的。
解释四:神经突触更新法则
这部分,是Hinton根据上面的一些假设,做出的一份合理神经突触工作机制的推测:
要点:
★First do an upward(forward) pass as usual.
分析:首先做正向传播。
★Then do top-down reconstruction at each level.
分析:在正向传播过程中,逐层贪心做Reconstruction(重构).
★Then perturb the top-level activities by blending them with the target values
so that the rate of change of activity of a top-level unit represents the derivative
of the error with respect to the total input to that unit.
-This will make the activity changes at every level represent error derivatives.
分析:到达最高层后,Target值和y形成时间导数,反向在各层传播,替代误差导数。
★Then update each synapse in proportion to:
$pre-synapse\,\, activty + \Delta Neruon=post-synapse \,\,activity$
分析:期间更新神经突触的状态,从pre(前状态)到post(后状态)。
解释五:自适应Pre-Training
生物神经的回炉机制从另一方面佐证了Pre-Traning的可能,于是出现了以下问题:
★This way of performing backpropagation appears to requires symmetric weights.
分析:回炉机制肯定需要两个对称的权值,正向权值&逆向权值
★What happens if the top-down weights are random and fixed?
分析:逆向权值如果是随机、且固定的,会怎么样?(即不存在自适应调整机制)
★Lillicrap,Cownden,Tweed&Akerman(2014)
showed that backprop still works almost as well.
-The bottom-up weights adapt so that the fixed top-down weights are approximately their
pseudo-inverse near the data mainfold.
分析:固定逆向权值,并不会造成太大影响。根据论文说法,最后正向权值矩阵会调整到与逆向权值矩阵互逆。
———————————————————————————————————————————————————
尽管固定逆向权值,并不会导致情况很糟糕,但是Hinton还是推荐逆向权值自适应调整,这贴合生物神经实际情况。
★If it works for fixed top-down weights,it must work for slowly changing top-down weights.
-So adapt the top-down weights to be good at reconstructing the activity in the layer below.
-This is just the wake-phase of the wake-sleep algorithm.
分析:自适应的逆向权值调整有利于重构。另外,这也是wake-sleep算法的醒状态。详见 [zouxy09] 的博客。
★With slowly apdapting top-down weights it works better.
在MNIST测试中:
-A 784-800-800-10 network with 50% dropout gets 153 errors.
-With fixed top-down pre-training,it gets 160 errors.
-With real adaptive backprop,it gets 150 errors and learns faster.
分析:从MNIST来看,自适应Pre-Traning还是不错的。
总结:脑皮层中的反向传播
放电信号不是大问题
★The fact that neurons send spikes rather than real numbers is not a problem
-Spikes are a great regularizer.
分析: 生物神经元放电, 而不是以实数计算. 并且电信号本身就是个很好的Weight调整约束器(regularizer).
时间导数
★Error derivatives can be represented as temporal derivatives.
-This allows a neuron to represent both its activity and its error derivative in the same axon.
分析: 误差导数可以被分解为线性时间导数, 这样, 一个神经元就无须准备传递两种Signal了.
$(temporal\_\_derivatives\quad \propto activity=y)$
放电时刻即是反向传播的时刻
★Spike-time dependent plasticity is the signature of backpropagation learning.
双向权值不是大问题
★The problem that each bottom-up connection needs to have a corresponding
top-down connection is a non-problem.
-Random top-down weights work just fine.
分析:生物神经网络中,逆向权值应该是存在的。即便逆向权值不能反向传播自适应调整,问题也不大。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号