【数据结构与算法】贪心算法详解

贪心算法详解

贪心算法（Greedy Algorithm）是一种在每一步选择中都采取当前状态下最优决策的算法策略，通过局部最优解的累积来逼近全局最优解。其核心思想是“着眼当下，不顾全局”，适用于具有贪心选择性质和最优子结构的问题。

---

核心原理

1. 贪心选择性质
   每一步的局部最优选择能导致全局最优解，无需回溯。

2. 最优子结构
   问题的最优解包含其子问题的最优解（与动态规划类似）。

---

执行流程

1. 问题分解
   将问题分解为多个相互关联的子问题。

2. 贪心策略
   对每个子问题应用贪心策略，做出当前最优选择。

3. 迭代求解
   基于前一步的结果，继续求解下一个子问题。

4. 组合解
   将所有局部最优解组合成最终解。

---

特性

特性	说明
高效性	时间复杂度通常较低（常为 O(n log n) 或 O(n)）
不可回溯	一旦做出选择，不可更改（与回溯、动态规划的区别）
局部最优导向	依赖局部最优决策，不保证全局最优（需证明正确性）
适用场景有限	仅适用于具有贪心选择性质的问题（如活动选择、霍夫曼编码）

---

适用场景

1. 活动选择问题
2. 霍夫曼编码
3. 最小生成树（Prim/Kruskal）
4. 单源最短路径（Dijkstra）
5. 部分背包问题（物品可拆分）

注意：贪心算法在 0-1背包问题 中不适用（物品不可拆分）。

---

经典问题：活动选择

问题描述
选择最多的互不重叠活动（每个活动有开始时间 s[i] 和结束时间 f[i]）。

贪心策略
优先选择结束时间最早的活动，为后续活动留出更多时间。

---

Java 代码实现

import java.util.*;

class Activity {
    int start;
    int end;
    
    public Activity(int start, int end) {
        this.start = start;
        this.end = end;
    }
}

public class GreedyActivitySelection {
    public static List<Activity> selectActivities(Activity[] activities) {
        // 1. 按结束时间升序排序
        Arrays.sort(activities, (a1, a2) -> Integer.compare(a1.end, a2.end));
        
        List<Activity> selected = new ArrayList<>();
        // 2. 选择第一个活动（结束最早）
        selected.add(activities[0]);
        int lastEnd = activities[0].end;
        
        // 3. 贪心选择后续活动
        for (int i = 1; i < activities.length; i++) {
            if (activities[i].start >= lastEnd) {
                selected.add(activities[i]);
                lastEnd = activities[i].end;
            }
        }
        return selected;
    }

    public static void main(String[] args) {
        Activity[] activities = {
            new Activity(1, 4), new Activity(3, 5),
            new Activity(0, 6), new Activity(5, 7),
            new Activity(8, 9), new Activity(5, 9)
        };
        
        List<Activity> result = selectActivities(activities);
        System.out.println("Selected Activities:");
        for (Activity act : result) {
            System.out.println("[" + act.start + ", " + act.end + "]");
        }
    }
}

---

代码解析

1. 排序阶段

   Arrays.sort(activities, (a1, a2) -> Integer.compare(a1.end, a2.end));
   

   按活动结束时间升序排序（贪心策略核心）。

2. 初始化选择

   selected.add(activities[0]);
   int lastEnd = activities[0].end;
   

   选择第一个结束最早的活动。

3. 贪心迭代

   if (activities[i].start >= lastEnd) {
        selected.add(activities[i]);
        lastEnd = activities[i].end;
   }
   

   后续活动只需满足开始时间 ≥ 上一个活动的结束时间。

---

输出结果

Selected Activities:
[1, 4]
[5, 7]
[8, 9]

---

贪心算法 vs 动态规划

特性	贪心算法	动态规划
决策依据	当前局部最优	历史状态 + 当前决策
回溯性	不可回溯	需保存子问题解（可回溯）
时间复杂度	通常更低	通常较高（需填表）
问题类型	满足贪心选择性质	有重叠子问题和最优子结构
解的正确性	需数学证明	天然保证最优解

---

贪心算法实战应用

贪心算法核心原理再探

贪心选择性质的数学证明

贪心算法的正确性依赖于两个关键性质，需要通过严格的数学证明：

1. 贪心选择性质证明（反证法示例）

假设存在一个最优解不包含贪心选择的第一步
证明将该最优解的第一个选择替换为贪心选择后：
  1. 新解仍然可行
  2. 新解的价值不低于原最优解
从而得出贪心选择是安全的

2. 最优子结构证明（递归关系）

设问题P的最优解为S
证明S包含子问题P'的最优解S'
若存在更优解S''，则可构造出比S更优的解，矛盾

贪心算法执行流程优化

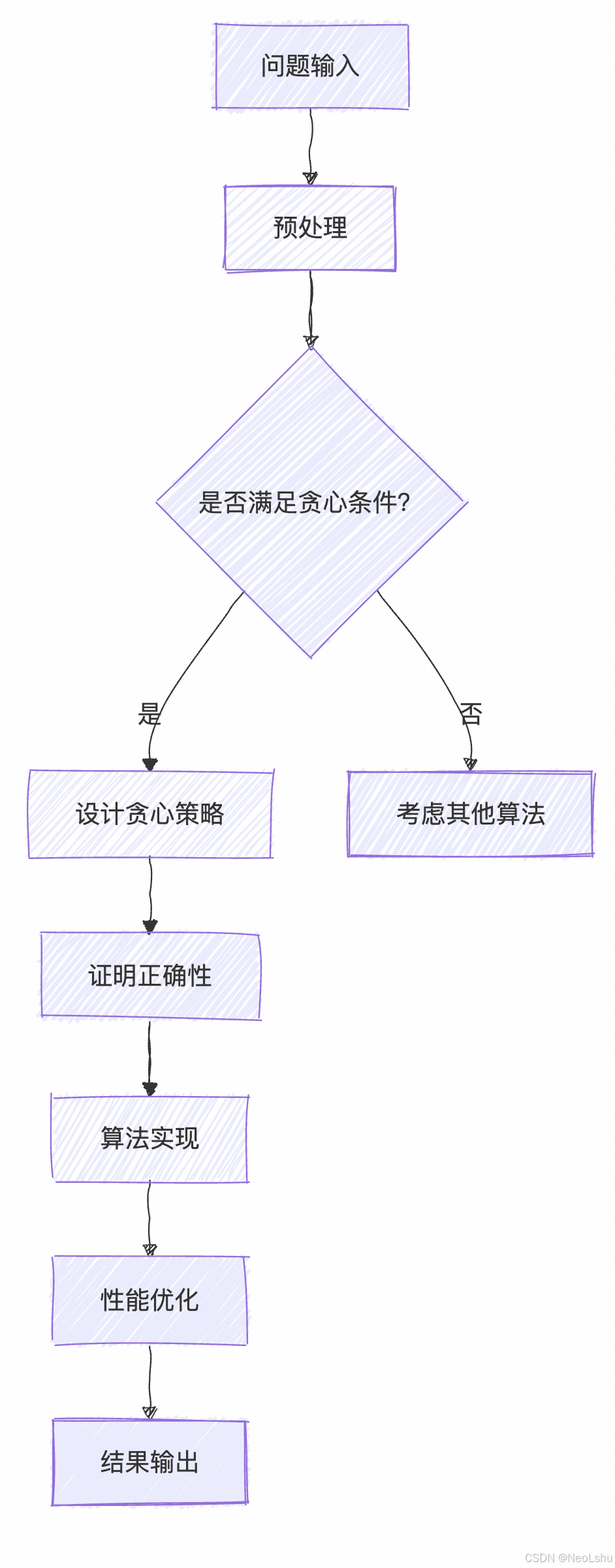
LeetCode贪心算法实战

1. 455. 分发饼干 (Assign Cookies)

问题描述：给孩子分配饼干，每个孩子有满足度g_i，饼干有大小s_j，每个孩子最多分一块饼干。求最多满足的孩子数。

贪心策略：

• 优先满足满足度小的孩子
• 使用能满足孩子的最小饼干

Java实现：

import java.util.Arrays;

public class AssignCookies {
    public int findContentChildren(int[] g, int[] s) {
        Arrays.sort(g);
        Arrays.sort(s);
        int child = 0, cookie = 0;
        while (child < g.length && cookie < s.length) {
            if (g[child] <= s[cookie]) {
                child++;
            }
            cookie++;
        }
        return child;
    }
}

复杂度分析：

• 时间复杂度：O(n log n + m log m) 排序时间复杂度
• 空间复杂度：O(1) 不使用额外空间

变种题：每个孩子可以分多块饼干（饼干可拆分），求最大满足度总和

public int maxSatisfaction(int[] g, int[] s) {
    Arrays.sort(g);
    Arrays.sort(s);
    int total = 0, j = 0;
    for (int i = 0; i < g.length && j < s.length; i++) {
        while (j < s.length && s[j] < g[i]) j++;
        if (j < s.length) {
            total += g[i];
            j++;
        }
    }
    return total;
}

2. 122. 买卖股票的最佳时机 II

问题描述：给定股票每天的价格，可进行多次交易（买前需卖出），求最大利润。

贪心策略：

• 所有上升趋势的收益都计入利润
• 忽略价格下跌的日子

Java实现：

public class BestTimeToBuyStock {
    public int maxProfit(int[] prices) {
        int profit = 0;
        for (int i = 1; i < prices.length; i++) {
            if (prices[i] > prices[i - 1]) {
                profit += prices[i] - prices[i - 1];
            }
        }
        return profit;
    }
}

复杂度分析：

• 时间复杂度：O(n) 单次遍历
• 空间复杂度：O(1) 常数空间

变种题：含交易手续费（714题）

public int maxProfit(int[] prices, int fee) {
    int buy = -prices[0]; // 持有股票状态
    int sell = 0;         // 不持有股票状态
    
    for (int i = 1; i < prices.length; i++) {
        int prevBuy = buy;
        buy = Math.max(buy, sell - prices[i]);
        sell = Math.max(sell, prevBuy + prices[i] - fee);
    }
    return sell;
}

3. 55. 跳跃游戏

问题描述：给定非负整数数组，每个元素表示可跳跃的最大长度，判断能否从起点到达终点。

贪心策略：

• 维护当前能到达的最远位置
• 遍历数组更新最远位置
• 当最远位置≥终点时返回true

Java实现：

public class JumpGame {
    public boolean canJump(int[] nums) {
        int maxReach = 0;
        for (int i = 0; i < nums.length; i++) {
            if (i > maxReach) return false;
            maxReach = Math.max(maxReach, i + nums[i]);
            if (maxReach >= nums.length - 1) return true;
        }
        return true;
    }
}

复杂度分析：

• 时间复杂度：O(n) 单次遍历
• 空间复杂度：O(1) 常数空间

变种题：45. 跳跃游戏 II（求最小跳跃次数）

public int jump(int[] nums) {
    int jumps = 0, curEnd = 0, curFarthest = 0;
    for (int i = 0; i < nums.length - 1; i++) {
        curFarthest = Math.max(curFarthest, i + nums[i]);
        if (i == curEnd) {
            jumps++;
            curEnd = curFarthest;
        }
    }
    return jumps;
}

4. 435. 无重叠区间

问题描述：给定区间集合，移除最小区间数使剩余区间互不重叠。

贪心策略：

• 按结束时间排序
• 优先保留结束早的区间
• 移除与已选区间重叠的区间

Java实现：

import java.util.Arrays;
import java.util.Comparator;

public class NonOverlappingIntervals {
    public int eraseOverlapIntervals(int[][] intervals) {
        if (intervals.length == 0) return 0;
        
        Arrays.sort(intervals, Comparator.comparingInt(a -> a[1]));
        int count = 1;
        int end = intervals[0][1];
        
        for (int i = 1; i < intervals.length; i++) {
            if (intervals[i][0] >= end) {
                count++;
                end = intervals[i][1];
            }
        }
        return intervals.length - count;
    }
}

复杂度分析：

• 时间复杂度：O(n log n) 排序时间复杂度
• 空间复杂度：O(1) 常数空间

变种题：452. 用最少数量的箭引爆气球

public int findMinArrowShots(int[][] points) {
    if (points.length == 0) return 0;
    
    Arrays.sort(points, (a, b) -> Integer.compare(a[1], b[1]));
    int arrows = 1;
    int end = points[0][1];
    
    for (int i = 1; i < points.length; i++) {
        if (points[i][0] > end) {
            arrows++;
            end = points[i][1];
        }
    }
    return arrows;
}

贪心算法高级应用

1. 霍夫曼编码优化（使用优先队列）

import java.util.PriorityQueue;

public class HuffmanOptimized {
    public int minCost(int[] freq) {
        PriorityQueue<Integer> pq = new PriorityQueue<>();
        for (int f : freq) pq.offer(f);
        
        int cost = 0;
        while (pq.size() > 1) {
            int a = pq.poll();
            int b = pq.poll();
            int sum = a + b;
            cost += sum;
            pq.offer(sum);
        }
        return cost;
    }
}

2. 任务调度问题（621. 任务调度器）

public class TaskScheduler {
    public int leastInterval(char[] tasks, int n) {
        int[] freq = new int[26];
        for (char c : tasks) freq[c - 'A']++;
        
        Arrays.sort(freq);
        int maxFreq = freq[25];
        int idleSlots = (maxFreq - 1) * n;
        
        for (int i = 24; i >= 0 && freq[i] > 0; i--) {
            idleSlots -= Math.min(maxFreq - 1, freq[i]);
        }
        
        return tasks.length + Math.max(0, idleSlots);
    }
}

贪心算法问题解决框架

1. 问题分析框架

graph TD
    A[问题分析] --> B{是否具有最优子结构？}
    B -->|是| C{是否具有贪心选择性质？}
    B -->|否| D[考虑动态规划或回溯]
    C -->|是| E[设计贪心策略]
    C -->|否| F[尝试动态规划]
    E --> G[证明正确性]
    G --> H[算法实现]

2. 代码实现模板

public class GreedyTemplate {
    public Solution greedySolution(Problem problem) {
        // 1. 预处理（通常需要排序）
        preprocess(problem);
        
        // 2. 初始化解决方案
        Solution solution = initializeSolution();
        
        // 3. 贪心迭代
        for (Element element : problem.getElements()) {
            if (isFeasible(solution, element)) {
                solution.add(element);
                updateState(solution, element);
            }
        }
        
        // 4. 返回结果
        return solution;
    }
}

总结与进阶

贪心算法适用场景特征

1. 局部最优可推导全局最优：问题具有贪心选择性质
2. 无后效性：当前决策不影响后续子问题
3. 高效性要求：需要优于O(n²)的解决方案
4. 问题可分解：问题可分解为相似子问题

贪心算法局限性

1. 不保证全局最优：局部最优的累积不一定全局最优
2. 证明困难：需要严格的数学证明
3. 适用范围有限：仅适用于特定问题类型
4. 对输入敏感：排序预处理可能增加时间复杂度

进阶学习方向

1. 拟阵理论：贪心算法的数学基础
2. 近似算法：贪心在NP难问题中的应用
3. 在线算法：处理流式数据的贪心策略
4. 分布式贪心：并行环境下的贪心算法

贪心算法作为算法设计的核心范式之一，其价值不仅在于解决特定问题，更在于培养"局部最优推导全局最优"的算法思维。掌握贪心算法的关键在于：准确识别适用场景、设计有效策略、严格证明正确性，并在实践中不断优化。