【数据结构与算法】分治算法深度解析与实战应用

分治算法核心原理

基本思想

分治算法（Divide and Conquer）是一种重要的算法设计范式，其核心思想是将一个复杂问题分解为若干个相同或相似的子问题，递归地解决这些子问题，最后将子问题的解合并得到原问题的解。

数学基础

分治算法的时间复杂度通常可以用递归关系式表示：

T(n) = aT(n/b) + f(n)

其中：

• a 是子问题的数量
• n/b 是每个子问题的规模
• f(n) 是分解和合并步骤的时间复杂度

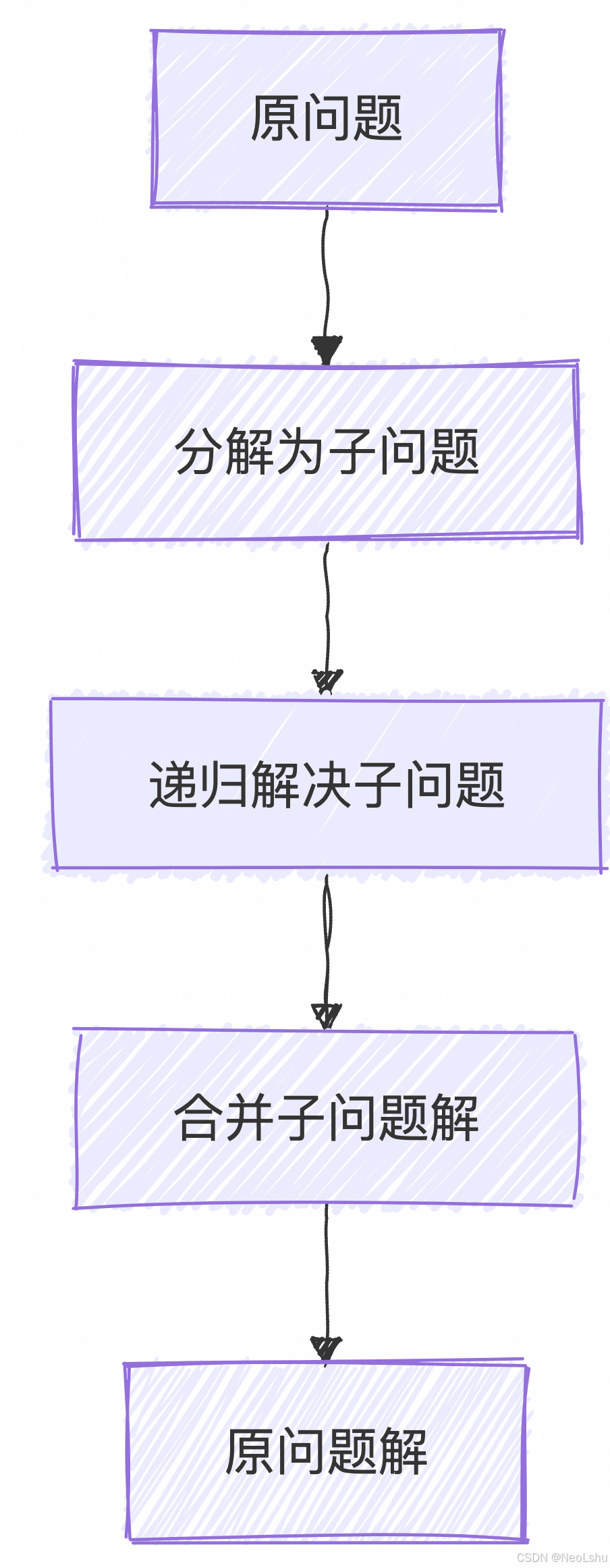
三个关键步骤

1. 分解（Divide）：将原问题分解为若干子问题
2. 解决（Conquer）：递归地解决各子问题
3. 合并（Combine）：将子问题的解合并为原问题的解

适用条件

1. 问题可分解为规模较小的相同子问题
2. 子问题相互独立（无重叠）
3. 子问题的解可以合并为原问题的解
4. 存在递归终止条件（基本情况）

与动态规划的区别

特性	分治算法	动态规划
子问题关系	相互独立	相互重叠
计算方式	递归计算	记忆化存储
最优子结构	不需要	必需
典型应用	归并排序、快速排序	背包问题、最短路径

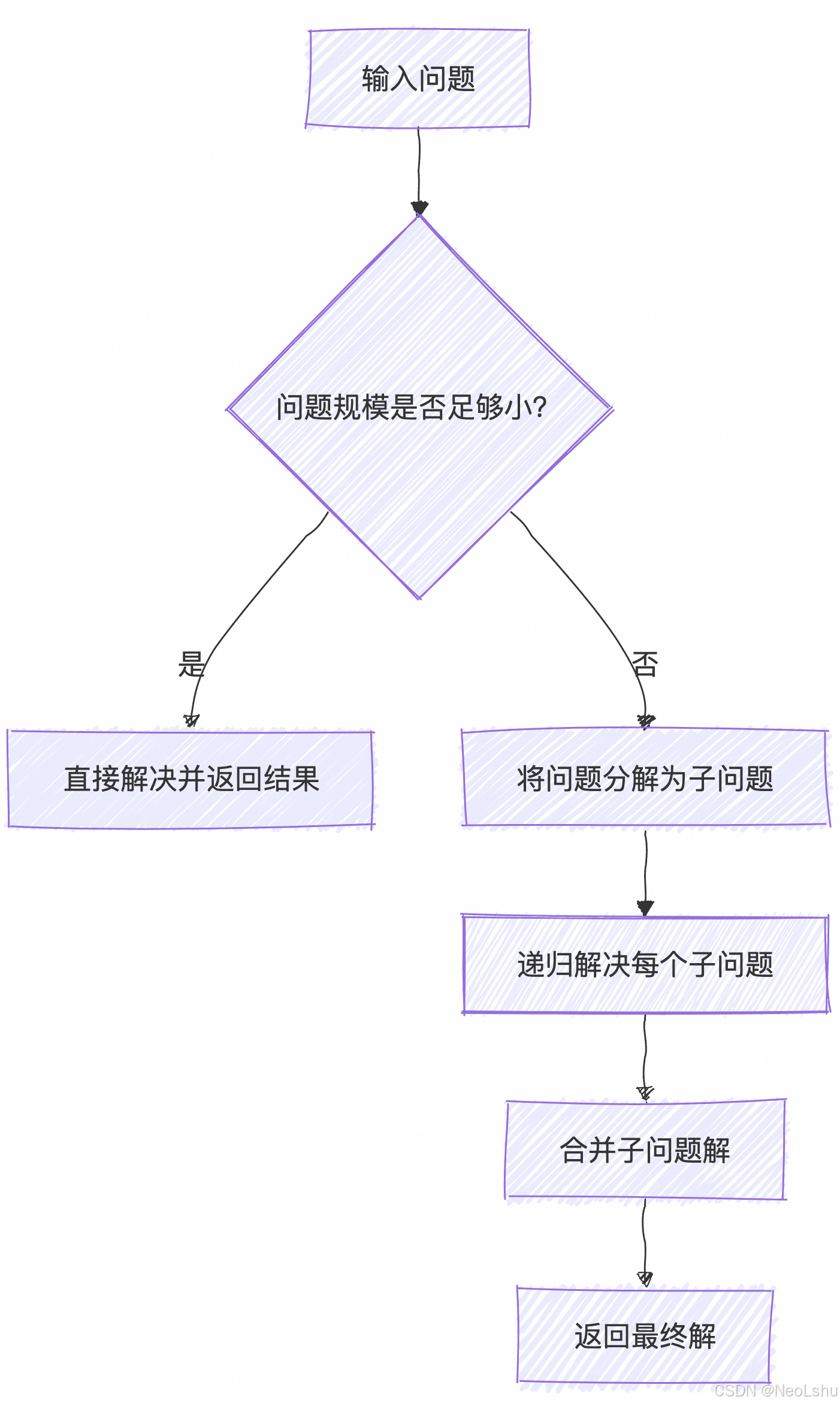
分治算法执行流程

标准执行流程

Java代码模板

public class DivideConquer {
    public Result solve(Problem problem) {
        // 基本情况：问题规模足够小，直接解决
        if (problem.isBaseCase()) {
            return solveBaseCase(problem);
        }
        
        // 分解：将问题分解为子问题
        Problem[] subproblems = divide(problem);
        
        // 解决：递归解决子问题
        Result[] results = new Result[subproblems.length];
        for (int i = 0; i < subproblems.length; i++) {
            results[i] = solve(subproblems[i]);
        }
        
        // 合并：将子问题的解合并
        return combine(results);
    }
    
    private Result solveBaseCase(Problem problem) {
        // 直接解决小规模问题
    }
    
    private Problem[] divide(Problem problem) {
        // 将问题分解为子问题
    }
    
    private Result combine(Result[] results) {
        // 合并子问题的解
    }
}

经典问题：归并排序

算法思想

1. 分解：将数组分成两半
2. 解决：递归排序两个子数组
3. 合并：合并两个已排序的子数组

Java实现

public class MergeSort {
    public void mergeSort(int[] arr) {
        if (arr.length > 1) {
            // 分解：将数组分成两半
            int mid = arr.length / 2;
            int[] left = Arrays.copyOfRange(arr, 0, mid);
            int[] right = Arrays.copyOfRange(arr, mid, arr.length);
            
            // 解决：递归排序子数组
            mergeSort(left);
            mergeSort(right);
            
            // 合并：合并已排序的子数组
            merge(arr, left, right);
        }
    }
    
    private void merge(int[] arr, int[] left, int[] right) {
        int i = 0, j = 0, k = 0;
        
        // 比较左右子数组元素并合并
        while (i < left.length && j < right.length) {
            if (left[i] <= right[j]) {
                arr[k++] = left[i++];
            } else {
                arr[k++] = right[j++];
            }
        }
        
        // 复制剩余元素
        while (i < left.length) {
            arr[k++] = left[i++];
        }
        while (j < right.length) {
            arr[k++] = right[j++];
        }
    }
}

复杂度分析

• 时间复杂度：O(n log n)
• 空间复杂度：O(n)

LeetCode分治算法实战

1. 53. 最大子序和（Maximum Subarray）

问题描述：给定整数数组，找到具有最大和的连续子数组。

分治解法

class Solution {
    public int maxSubArray(int[] nums) {
        return maxSubArray(nums, 0, nums.length - 1);
    }
    
    private int maxSubArray(int[] nums, int left, int right) {
        if (left == right) {
            return nums[left];
        }
        
        int mid = left + (right - left) / 2;
        
        // 递归求解左右子数组的最大子序和
        int leftMax = maxSubArray(nums, left, mid);
        int rightMax = maxSubArray(nums, mid + 1, right);
        
        // 计算跨越中点的最大子序和
        int crossMax = crossSum(nums, left, right, mid);
        
        // 返回三者中的最大值
        return Math.max(Math.max(leftMax, rightMax), crossMax);
    }
    
    private int crossSum(int[] nums, int left, int right, int mid) {
        // 向左扩展的最大和
        int leftSum = Integer.MIN_VALUE;
        int sum = 0;
        for (int i = mid; i >= left; i--) {
            sum += nums[i];
            leftSum = Math.max(leftSum, sum);
        }
        
        // 向右扩展的最大和
        int rightSum = Integer.MIN_VALUE;
        sum = 0;
        for (int i = mid + 1; i <= right; i++) {
            sum += nums[i];
            rightSum = Math.max(rightSum, sum);
        }
        
        return leftSum + rightSum;
    }
}

复杂度分析：

• 时间复杂度：O(n log n)
• 空间复杂度：O(log n)（递归调用栈）

变种题：152. 乘积最大子数组

class Solution {
    public int maxProduct(int[] nums) {
        return maxProduct(nums, 0, nums.length - 1);
    }
    
    private int maxProduct(int[] nums, int left, int right) {
        if (left == right) return nums[left];
        
        int mid = left + (right - left) / 2;
        int leftMax = maxProduct(nums, left, mid);
        int rightMax = maxProduct(nums, mid + 1, right);
        int crossMax = crossProduct(nums, left, right, mid);
        
        return Math.max(Math.max(leftMax, rightMax), crossMax);
    }
    
    private int crossProduct(int[] nums, int left, int right, int mid) {
        int leftMin = nums[mid], leftMax = nums[mid];
        int prod = 1;
        for (int i = mid; i >= left; i--) {
            prod *= nums[i];
            leftMin = Math.min(leftMin, prod);
            leftMax = Math.max(leftMax, prod);
        }
        
        int rightMin = nums[mid+1], rightMax = nums[mid+1];
        prod = 1;
        for (int i = mid+1; i <= right; i++) {
            prod *= nums[i];
            rightMin = Math.min(rightMin, prod);
            rightMax = Math.max(rightMax, prod);
        }
        
        return Math.max(leftMax * rightMax, leftMin * rightMin);
    }
}

2. 215. 数组中的第K个最大元素（Kth Largest Element in an Array）

问题描述：在未排序数组中找到第k个最大的元素。

分治解法（快速选择）

class Solution {
    public int findKthLargest(int[] nums, int k) {
        return quickSelect(nums, 0, nums.length - 1, nums.length - k);
    }
    
    private int quickSelect(int[] nums, int left, int right, int k) {
        if (left == right) return nums[left];
        
        int pivotIndex = partition(nums, left, right);
        
        if (k == pivotIndex) {
            return nums[k];
        } else if (k < pivotIndex) {
            return quickSelect(nums, left, pivotIndex - 1, k);
        } else {
            return quickSelect(nums, pivotIndex + 1, right, k);
        }
    }
    
    private int partition(int[] nums, int left, int right) {
        int pivot = nums[right];
        int i = left;
        
        for (int j = left; j < right; j++) {
            if (nums[j] <= pivot) {
                swap(nums, i, j);
                i++;
            }
        }
        
        swap(nums, i, right);
        return i;
    }
    
    private void swap(int[] nums, int i, int j) {
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }
}

复杂度分析：

• 平均时间复杂度：O(n)
• 最坏时间复杂度：O(n²)
• 空间复杂度：O(1)

变种题：973. 最接近原点的K个点

class Solution {
    public int[][] kClosest(int[][] points, int k) {
        quickSelect(points, 0, points.length - 1, k);
        return Arrays.copyOf(points, k);
    }
    
    private void quickSelect(int[][] points, int left, int right, int k) {
        if (left >= right) return;
        
        int pivotIndex = partition(points, left, right);
        
        if (pivotIndex == k) {
            return;
        } else if (pivotIndex > k) {
            quickSelect(points, left, pivotIndex - 1, k);
        } else {
            quickSelect(points, pivotIndex + 1, right, k);
        }
    }
    
    private int partition(int[][] points, int left, int right) {
        int pivot = distance(points[right]);
        int i = left;
        
        for (int j = left; j < right; j++) {
            if (distance(points[j]) < pivot) {
                swap(points, i, j);
                i++;
            }
        }
        
        swap(points, i, right);
        return i;
    }
    
    private int distance(int[] point) {
        return point[0] * point[0] + point[1] * point[1];
    }
    
    private void swap(int[][] points, int i, int j) {
        int[] temp = points[i];
        points[i] = points[j];
        points[j] = temp;
    }
}

3. 241. 为运算表达式设计优先级（Different Ways to Add Parentheses）

问题描述：给定一个包含数字和运算符的字符串，为表达式添加括号以改变运算顺序，返回所有可能的结果。

分治解法

class Solution {
    public List<Integer> diffWaysToCompute(String expression) {
        List<Integer> results = new ArrayList<>();
        
        for (int i = 0; i < expression.length(); i++) {
            char c = expression.charAt(i);
            
            if (c == '+' || c == '-' || c == '*') {
                // 分解：以运算符为界分解表达式
                String leftExpr = expression.substring(0, i);
                String rightExpr = expression.substring(i + 1);
                
                // 解决：递归计算左右表达式
                List<Integer> leftResults = diffWaysToCompute(leftExpr);
                List<Integer> rightResults = diffWaysToCompute(rightExpr);
                
                // 合并：根据运算符组合结果
                for (int left : leftResults) {
                    for (int right : rightResults) {
                        switch (c) {
                            case '+': results.add(left + right); break;
                            case '-': results.add(left - right); break;
                            case '*': results.add(left * right); break;
                        }
                    }
                }
            }
        }
        
        // 基本情况：表达式为单个数字
        if (results.isEmpty()) {
            results.add(Integer.parseInt(expression));
        }
        
        return results;
    }
}

复杂度分析：

• 时间复杂度：O(Cₙ)（卡特兰数）
• 空间复杂度：O(Cₙ)

变种题：95. 不同的二叉搜索树 II

class Solution {
    public List<TreeNode> generateTrees(int n) {
        if (n == 0) return new ArrayList<>();
        return generateTrees(1, n);
    }
    
    private List<TreeNode> generateTrees(int start, int end) {
        List<TreeNode> trees = new ArrayList<>();
        
        if (start > end) {
            trees.add(null);
            return trees;
        }
        
        for (int i = start; i <= end; i++) {
            // 分解：递归构建左右子树
            List<TreeNode> leftTrees = generateTrees(start, i - 1);
            List<TreeNode> rightTrees = generateTrees(i + 1, end);
            
            // 合并：以i为根节点组合左右子树
            for (TreeNode left : leftTrees) {
                for (TreeNode right : rightTrees) {
                    TreeNode root = new TreeNode(i);
                    root.left = left;
                    root.right = right;
                    trees.add(root);
                }
            }
        }
        
        return trees;
    }
}

4. 23. 合并K个升序链表（Merge k Sorted Lists）

问题描述：合并k个有序链表为一个有序链表。

分治解法

class Solution {
    public ListNode mergeKLists(ListNode[] lists) {
        if (lists == null || lists.length == 0) return null;
        return mergeLists(lists, 0, lists.length - 1);
    }
    
    private ListNode mergeLists(ListNode[] lists, int left, int right) {
        if (left == right) return lists[left];
        
        int mid = left + (right - left) / 2;
        
        // 分解：递归合并左右两部分
        ListNode leftList = mergeLists(lists, left, mid);
        ListNode rightList = mergeLists(lists, mid + 1, right);
        
        // 合并：合并两个有序链表
        return mergeTwoLists(leftList, rightList);
    }
    
    private ListNode mergeTwoLists(ListNode l1, ListNode l2) {
        ListNode dummy = new ListNode(0);
        ListNode current = dummy;
        
        while (l1 != null && l2 != null) {
            if (l1.val < l2.val) {
                current.next = l1;
                l1 = l1.next;
            } else {
                current.next = l2;
                l2 = l2.next;
            }
            current = current.next;
        }
        
        current.next = (l1 != null) ? l1 : l2;
        return dummy.next;
    }
}

复杂度分析：

• 时间复杂度：O(N log k)（N为总节点数，k为链表数）
• 空间复杂度：O(log k)（递归调用栈）

变种题：315. 计算右侧小于当前元素的个数

class Solution {
    private int[] count;
    
    public List<Integer> countSmaller(int[] nums) {
        count = new int[nums.length];
        int[] indexes = new int[nums.length];
        for (int i = 0; i < nums.length; i++) indexes[i] = i;
        
        mergeSort(nums, indexes, 0, nums.length - 1);
        
        List<Integer> result = new ArrayList<>();
        for (int c : count) result.add(c);
        return result;
    }
    
    private void mergeSort(int[] nums, int[] indexes, int start, int end) {
        if (start >= end) return;
        
        int mid = start + (end - start) / 2;
        mergeSort(nums, indexes, start, mid);
        mergeSort(nums, indexes, mid + 1, end);
        
        merge(nums, indexes, start, end);
    }
    
    private void merge(int[] nums, int[] indexes, int start, int end) {
        int mid = start + (end - start) / 2;
        int left = start;
        int right = mid + 1;
        int[] newIndexes = new int[end - start + 1];
        int idx = 0;
        int rightCount = 0;
        
        while (left <= mid && right <= end) {
            if (nums[indexes[right]] < nums[indexes[left]]) {
                newIndexes[idx] = indexes[right];
                rightCount++;
                right++;
            } else {
                newIndexes[idx] = indexes[left];
                count[indexes[left]] += rightCount;
                left++;
            }
            idx++;
        }
        
        while (left <= mid) {
            newIndexes[idx] = indexes[left];
            count[indexes[left]] += rightCount;
            left++;
            idx++;
        }
        
        while (right <= end) {
            newIndexes[idx] = indexes[right];
            right++;
            idx++;
        }
        
        System.arraycopy(newIndexes, 0, indexes, start, end - start + 1);
    }
}

分治算法优化策略

1. 减少递归调用

// 优化后的归并排序
public void optimizedMergeSort(int[] arr, int left, int right) {
    // 小规模数组使用插入排序
    if (right - left < 20) {
        insertionSort(arr, left, right);
        return;
    }
    
    int mid = (left + right) / 2;
    optimizedMergeSort(arr, left, mid);
    optimizedMergeSort(arr, mid + 1, right);
    
    // 优化：只有需要时才合并
    if (arr[mid] > arr[mid + 1]) {
        merge(arr, left, mid, right);
    }
}

2. 并行化处理

// 并行归并排序
public void parallelMergeSort(int[] arr, int left, int right, int depth) {
    if (depth <= 0 || right - left < 1000) {
        mergeSort(arr, left, right);
        return;
    }
    
    int mid = (left + right) / 2;
    
    Thread leftThread = new Thread(() -> 
        parallelMergeSort(arr, left, mid, depth - 1));
    Thread rightThread = new Thread(() -> 
        parallelMergeSort(arr, mid + 1, right, depth - 1));
    
    leftThread.start();
    rightThread.start();
    
    try {
        leftThread.join();
        rightThread.join();
    } catch (InterruptedException e) {
        Thread.currentThread().interrupt();
    }
    
    merge(arr, left, mid, right);
}

分治算法总结

适用场景

1. 问题可分解为相同子问题
2. 子问题相互独立
3. 子问题解可合并
4. 问题规模较大，需要高效解法

优势与局限

优势	局限
简化复杂问题	递归调用开销大
高效解决大规模问题	子问题必须独立
天然适合并行计算	合并步骤可能复杂
代码结构清晰	空间复杂度较高

关键要点

1. 正确分解问题：确保子问题与原问题同构
2. 合理设置基本情况：处理小规模问题
3. 高效合并解：设计优化的合并策略
4. 避免重复计算：确保子问题相互独立

分治算法通过"分而治之"的策略，将复杂问题分解为可管理的子问题，是解决大规模计算问题的强大工具。掌握分治算法的核心思想和实现技巧，能够有效提升解决复杂问题的能力。