洛谷P1970 花匠

题目描述

花匠栋栋种了一排花，每株花都有自己的高度。花儿越长越大，也越来越挤。栋栋决定把这排中的一部分花移走，将剩下的留在原地，使得剩下的花能有空间长大，同时，栋栋希望剩下的花排列得比较别致。

具体而言，栋栋的花的高度可以看成一列整数h_1,h_2,...,h_nh1​,h2​,...,hn​。设当一部分花被移走后，剩下的花的高度依次为g_1,g_2,...,g_mg1​,g2​,...,gm​，则栋栋希望下面两个条件中至少有一个满足：

条件 AA：对于所有g_{2i}>g_{2i-1},g_{2i}>g_{2i+1}g2i​>g2i−1​,g2i​>g2i+1​

条件 BB：对于所有g_{2i}<g_{2i-1},g_{2i}<g_{2i+1}g2i​<g2i−1​,g2i​<g2i+1​

注意上面两个条件在m=1m=1时同时满足，当m > 1m>1时最多有一个能满足。

请问，栋栋最多能将多少株花留在原地。

输入格式

第一行包含一个整数nn，表示开始时花的株数。

第二行包含nn个整数，依次为h_1,h_2,...,h_nh1​,h2​,...,hn​,表示每株花的高度。

输出格式

一个整数mm，表示最多能留在原地的花的株数。

---

 

将花的高度记成一张折线图。

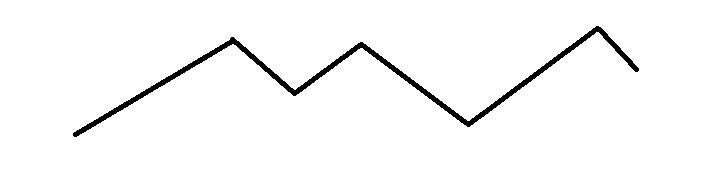
题意就是求这样一段曲折的数据波动的次数。

对于第每一段，取这段的任何一个点/波峰/波谷都不会对答案产生影响。

所以题目的意思就是求一段数据的波峰波谷的数量。

#include<iostream>
using namespace std;
int n,q[1000005],ans=1;
bool p;
int main()
{
    cin>>n;
    for(int i=1;i<=n;i++) 
        cin>>q[i];
    if(q[2]>=q[1]) 
        p=1;
    for(int i=1;i<=n;i++)
    {
        if(p==0&&i==n)
        {
            ans++;
            break;
        }
        if(p==1&&q[i+1]<q[i]) 
            {
                ans++;
                p=0;
            }
        else if(p==0&&q[i+1]>q[i]) 
            {
                ans++;
                p=1;
            }
    }
    cout<<ans; 
}