圆锥曲线 随缘一题(2)

21

(1)

\[|MF|=|MP| \Rightarrow |MF|-|ME|=|EP|=2 \Rightarrow C:x^2-\frac{y^2}{3}=1 \]

(2)

---

其他的存档：

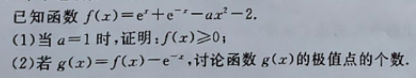
22

(1)

\[a=1 \Rightarrow f(x)=e^x+e^{-x}-x^2-2 \Rightarrow f'(x)=e^x-e^{-x}-2x \\ \Rightarrow f''(x)=e^x+e^{-x}-2 \ge 2\sqrt{e^xe^{-x}}-2=0 \\ \Rightarrow f'(x)单调增,f'(0)=0 \Rightarrow f(x)_{\min}=f(0)=0 \Rightarrow f(x) \ge 0 \]

(2)

\[g(x)=e^x-ax^2-2 \Rightarrow g'(x)=e^x-2ax \Rightarrow g''(x)=e^x-2a \\ 1^\circ \,\, a \lt 0:g''(x) \ge 0 \Rightarrow g'(x)单调增,g'(+\infty)>0,g'(-\infty)<0 \\ \Rightarrow 所以g(x)只有一个极小值点,无极大值点 \\ 2^\circ \,\, a=0: g'(x)=e^x>0 \Rightarrow 所以g(x)无极值点 \\ 3^\circ \,\, a>0:g''(x)有零点x_0=\ln (2a),g'(x)在(-\infty,\ln2a)单调减,在(\ln 2a,+\infty) 单调增 \\ g'(+\infty)>0,g'(-\infty)>0,g'(\ln 2a)=2a-2a\ln2a=2a(1-\ln 2a) \\ 当0<a\le \frac{e}{2}时,g'(\ln 2a)\ge 0,g(x)无极值点 \\ 当a>\frac{e}{2}时,g'(\ln 2a)<0,g(x)有一个极大值点和一个极小值点 \]

18

(1)

\[b=\sqrt{5}a\sin B \Rightarrow1=\sin B=\sqrt{5}\sin A\sin B \Rightarrow \sin A=\frac{1}{\sqrt{5}} \\ \Rightarrow \sin B=\sin(A+C)=\frac{1}{\sqrt{2}}\left(-\frac{1}{\sqrt{5}}+\frac{2}{\sqrt{5}}\right)=\frac{\sqrt{10}}{10} \]

(2)

\[b=\sqrt{5}a\sin B=\frac{1}{\sqrt{2}}a \Rightarrow a=\sqrt{2}b \\ c=\frac{\sin C}{\sin B}b=\sqrt{5}b \\ \text{let: }2x=c=\sqrt{5}b \\ \text{consider: } \cos\angle ADC+\cos \angle BDC=0 \Rightarrow \frac{x^2+1-b^2}{2x}+\frac{x^2+1-2b^2}{2x}=0 \Rightarrow b=2 \\ S=\frac{1}{2}ab\sin C=2 \]