微积分(A)每日一题[42]

\[\begin{aligned} &\text{Part I.} \\ &\int_0^{A}\frac{f'(x)}{f^2(x)}dx=-\frac{1}{f(x)} \bigg|_0^A=\frac{1}{f(0)}-\frac{1}{f(A)} \\ &\int_{0}^{+\infty}\frac{f'(x)}{f^2(x)}dx=\lim_{A \to +\infty} \left(\frac{1}{f(0)}-\frac{1}{f(A)}\right) 收敛(单调有界则极限存在) \\ \\ &\text{Part II.} \\ &\frac{1}{f(x)}-\frac{1}{f(x)+f'(x)}=\frac{f'(x)}{f^2(x)+f(x)f'(x)} \le \frac{f'(x)}{f^2(x)} \\ &0 < \frac{1}{f(x)} \le \frac{f'(x)}{f^2(x)}+\frac{1}{f(x)+f'(x)} \\ &\int_0^{+\infty}\frac{f'(x)}{f^2(x)}dx,\int_0^{+\infty}\frac{1}{f(x)+f'(x)}dx 收敛 \\ & 故 \int_0^{+\infty} \frac{1}{f(x)}dx 收敛 \end{aligned} \]

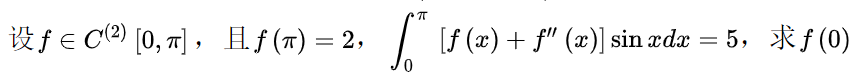
\[\begin{aligned} \int_0^{\pi}f''(x)\sin xdx &=f'(x)\sin x\bigg|_0^{\pi}-\int_0^\pi f'(x)\cos xdx \\ &=-f(x)\cos x\bigg|_0^\pi+\int_0^{\pi}f(x)(-\sin x)dx \\ \Rightarrow &f(\pi)+f(0)=\int_0^{\pi}[f(x)+f''(x)]\sin xdx=5 \\ \Rightarrow &f(0)=3 \end{aligned} \]