微积分(A)每日一题[37]

微分方程习题课

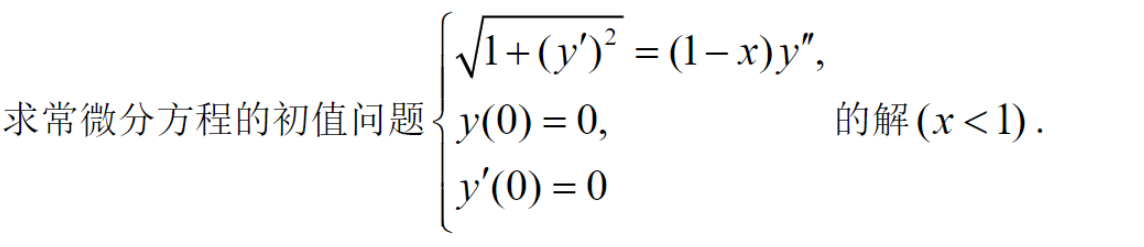
小技巧：\(h+\sqrt{h^2-1}=g \Rightarrow (g-h)^2=\sqrt{h^2-1} \Rightarrow g^2-2gh+{\color{red}{h^2}}={\color{red}{h^2}}-1\)

\[\begin{aligned} &p=y' \\ &\sqrt{1+p^2}=(1-x)\frac{dp}{dx} \\ &-\ln|1-x|=\int \frac{dp}{\sqrt{1+p^2}}=\ln |p+\sqrt{p^2+1}|+C_1 \\ &\frac{C_2}{1-x}=p+\sqrt{p^2+1} \\ &\left( \frac{C_2}{1-x}-p \right)=\sqrt{p^2+1} \\ &\frac{C_2^2}{(1-x)^2}+p^2-\frac{2C_2}{1-x}p=p^2+1 \\ &y'=p=\frac{1-x}{2C_2}\frac{C_2^2}{(1-x)^2}-\frac{1-x}{2C_2}=\frac{C_2}{2(1-x)}+\frac{x-1}{2C_2} \\ &y=-\frac{C_2}{2}\ln|1-x|+\frac{(x-1)^2}{4C_2}+C_3 \end{aligned} \]

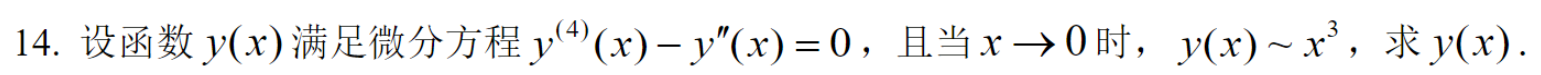
\[\begin{aligned} &p=y'' \\ &y^{(4)}-y''(x)=0 \Rightarrow p''=p \\ &\lambda ^2-1=0 \Rightarrow \lambda =\pm 1 \Rightarrow p=C_1e^x+C_2e^{-x} \\ &y''(x)=C_1e^x+C_2e^{-x} \\ &y'''(x)=C_1e^x-C_2e^{-x} \\ &y'(x)=C_1e^x-C_2e^{-x}+C_3 \\ &y(x)=C_1e^x+C_2e^{-x}+C_3x+C_4 \\ &y(0)=y'(0)=y''(0)=0,y'''(0)=1 \\ &C_1=3,C_2=-3,C_3=-6,C_4=0 \\ &y(x)=3(e^x-e^{-x}-2x) \\ &\text{其实也不用这么麻烦，直接解四阶线性常微分方程就行。}\\ \end{aligned} \]