微积分(A)随缘一题[32]

1

设切于 \((x_0,\ln x_0)\)，则 \(l:y=\frac{1}{x_0}(x-x_0)+\ln x_0(2 \le x_0 \le 6)\)

\[\begin{aligned} S=S(x_0)=&\int_2^6 \left(\frac{x-x_0}{x_0}+\ln x_0-\ln x \right)dx \\ =&\left( \frac{(x-x_0)^2}{2x_0}+x\ln x_0-x\ln x+x \right)\bigg|_2^6 \\ =&\frac{(6-x_0)^2-(2-x_0)^2}{2x_0}+4\ln x_0+4-6\ln 6+2\ln 2 \\ =&\frac{16}{x_0}+4\ln x_0+(2\ln 2-6\ln 6) \end{aligned} \]

所以：\(S'(x)=-\frac{16}{x^2}+\frac{4}{x}=\frac{4(x-4)}{x^2}\)

所以取 \(x_0=4\)，则 \(l:y=\frac{x}{4}-1+2\ln 2\)

2

(1)

\[\begin{aligned} L =&\int_0^{2\pi} \sqrt{[x'(t)]^2+[y'(t)]^2}dt \\ =&\int_0^{2\pi} \sqrt{(1-\cos t)^2+(\sin t)^2} dt \\ =&\int_0^{2\pi} \sqrt{2-2\cos t} dt \\ =&\int_0^{2\pi} \sqrt{2(2\sin^2 \frac{t}{2})} dt \\ =&4\int_0^{2\pi} \sin \frac{t}{2} d\frac{t}{2} \\ =&-4\cos \frac{t}{2} \bigg|_0^{2\pi} \\ =&-4(-1-1)=8 \end{aligned} \]

(2)

\[\begin{aligned} S \xlongequal{x'(t) \ge 0}&\int_0^{2\pi}y(t)x'(t)dt \\ =&\int_0^{2\pi}(1-\cos t)^2dt \\ =&8\int_0^{2\pi}\sin^4\frac{t}{2} d\frac{t}{2} \\ =&16\int_0^{\frac{\pi}{2}} \sin^4 tdt \\ =&16 \frac{3!!}{4!!}\frac{\pi}{2} \\ =&3\pi \end{aligned} \]

3

\[\begin{aligned} &y'(t)=\left(e^t \int_{\frac{\pi}{2}}^{t}\frac{\cos2u}{e^u}du \right)'=e^t \int_\frac{\pi}{2}^t\frac{\cos 2u}{e^u}du+e^t\frac{\cos 2t}{e^t} \Rightarrow y'(\frac{\pi}{2})=\cos \pi=-1 \\ &x'(t)=e^t\int_\frac{\pi}{2}^t\frac{\sin \frac{u}{3}}{e^u}du+e^t \frac{\sin \frac{u}{3}}{e^t} \Rightarrow x'(\frac{\pi}{2})=\sin \frac{\pi}{6}=\frac{1}{2} \\ &k=\frac{dy}{dx}=\frac{\frac{dy}{dt}}{\frac{dx}{dt}}=\frac{y'(\frac{\pi}{2})}{x'(\frac{\pi}{2})}=-2 \\ &x(\frac{\pi}{2})=y(\frac{\pi}{2})=0 \\ &l_{切}: y=-2x \\ &l_{法}: y=\frac{x}{2} \end{aligned} \]

4

即：\(D=\{(x,y)|(x-1)^2+y^2 \le 1,y \ge x\}\)

\[\begin{aligned} V =& \pi \int_0^1 ((2-(1-\sqrt{1-y^2}))^2-(2-y)^2)dy \\ =& \pi \int_0^1 ( -2-2y^2+4y+2\sqrt{1-y^2} ) dy \\ =& \pi (-2 - \frac{2}{3} +2 +\frac{\pi}{2} ) \\ =& \frac{\pi^2}{2}-\frac{2\pi}{3} \end{aligned} \]

5

(1)

设切于点 \((x_0,\sqrt{x_0-2})\)，切线为 \(l:x=2\sqrt{x_0-2}y+1\)

所以：\(x_0=2(x_0-2)+1 \Rightarrow x_0=3 \Rightarrow l:x=2y+1\)

\[\begin{aligned} S =& \int_1^{3} \frac{x-1}{2} dx-\int_2^3 \sqrt{x-2} dx \\ =& 1-\left( \frac{(x-2)^\frac{3}{2}}{\frac{3}{2}} \bigg|_2^3 \right) \\ =& \frac{1}{3} \end{aligned} \]

(2)

\[\begin{aligned} V =& \pi \int_1^{3} (\frac{x-1}{2})^2 dx-\pi \int_2^3 (\sqrt{x-2})^2 dx \\ =& \frac{2\pi}{3}-\frac{\pi}{2} \\ =& \frac{\pi}{6} \end{aligned} \]

(3)

\[\begin{aligned} V =&\int_1^3 2\pi x \frac{x-1}{2}dx-\int_2^3 2\pi x \sqrt{x-2}dx \\ =& \frac{14\pi}{3}-\frac{52\pi}{15} \\ =& \frac{6\pi}{5} \end{aligned} \]

6

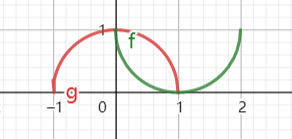
\[\begin{aligned} V =& \frac{1}{2} \frac{4}{3}\pi 1^3-\pi \int_0^1 (1-\sqrt{2x-x^2})^2 dx \\ =& \frac{2\pi}{3}-\pi \int_{-1}^0 (1-\sqrt{1-x^2})^2dx \\ =& \frac{2\pi}{3}-\pi \int_{-1}^0 (2-x^2-2\sqrt{1-x^2})dx \\ =& \frac{2\pi}{3}-\pi (2-\frac{1}{3}-2 \frac{1}{4} \pi 1^2) \\ =& \frac{\pi^2}{2}-\pi \end{aligned} \]

\[\begin{aligned} S =& \frac{1}{2}4\pi 1^2+2\pi\int_0^1 (1-\sqrt{2x-x^2}) \sqrt{1+(\frac{2-2x}{2\sqrt{2x-x^2}})^2}dx \\ =& 2\pi+2\pi\int_0^1(1-\sqrt{1-(x-1)^2}) \sqrt{1+\frac{(x-1)^2}{1-(x-1)^2}}dx \\ =&2\pi+2\pi\int_{-1}^0(1-\sqrt{1-x^2}) \sqrt{1+\frac{x^2}{1-x^2}}dx \\ =&2\pi+2\pi\int_{-1}^0 \frac{1-\sqrt{1-x^2}}{\sqrt{1-x^2}}dx \\ =&2\pi\int_{-1}^0 \frac{1}{\sqrt{1-x^2}}dx \\ =&2\pi \arcsin x\bigg|_{-1}^0 \\ =&\pi^2 \end{aligned} \]

7

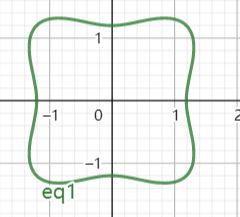
\[\begin{aligned} &x=\rho \cos \theta,y=\rho \sin \theta \Rightarrow \rho^2 (\cos^4\theta+\sin^4 \theta)=a^2 \\ &\begin{aligned} \int \frac{dx}{\sin^4x+\cos^4x} =&\int \frac{\tan^2x+1}{\tan^4x+1}d\tan x \xlongequal{t=\tan x}\int \frac{t^2+1}{t^4+1}dt \\ =& \int \frac{1+t^{-2}}{t^2+t^{-2}}dt \\ =&\int \frac{d(t-t^{-1})}{(t-t^{-1})^2+2} \\ =&\frac{\arctan \frac{t-t^{-1}}{\sqrt{2}}}{\sqrt{2}} \\ =&\frac{\sqrt{2}}{2} \arctan \frac{\tan x-\frac{1}{\tan x}}{\sqrt{2}} \end{aligned} \\ &\begin{aligned} S =&4\int_0^{\frac{\pi}{2}} \frac{1}{2} \rho^2 d\theta \\ =&2a^2\int_0^{\frac{\pi}{2}}\frac{d\theta}{\sin^4 \theta+\cos^4\theta} \\ =&2a^2 \frac{\sqrt{2}}{2} \left( \arctan \frac{\tan x-\frac{1}{\tan x}}{\sqrt{2}} \bigg|_0^{\frac{\pi}{2}}\right) \\ =&\sqrt{2}a^2 (\arctan (+\infty)-\arctan(-\infty)) \\ =&\sqrt{2}\pi a^2 \end{aligned} \end{aligned} \]

8

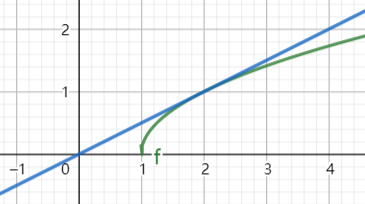
\[\begin{aligned} &l:y=\frac{1}{2\sqrt{x_0-1}}x,(x_0,\sqrt{x_0-1}) \in l \Rightarrow l:y=\frac{x}{2} \Rightarrow \\ &\begin{aligned} S =&2\pi \int_0^2 \frac{x}{2} \sqrt{1+(\frac{1}{2})^2}dx+2\pi \int_1^{2} \sqrt{x-1}\sqrt{1+(\frac{1}{2\sqrt{x-1}})^2}dx \\ =&\sqrt{5}\pi+\pi \int_1^2 \sqrt{x-1}\sqrt{\frac{4x-3}{x-1}}dx \\ =&\sqrt{5}\pi+\frac{\pi}{4} \int_1^2 \sqrt{4x-3} d(4x-3) \\ =&\sqrt{5}\pi+\frac{\pi}{4} \left( \frac{(4x-3)^{\frac{3}{2}}}{\frac{3}{2}} \bigg|_1^{2} \right) \\ =&\sqrt{5}\pi+\frac{\pi}{6}(5\sqrt{5}-1) \\ =&\frac{11\sqrt{5}-1}{6}\pi \end{aligned} \end{aligned} \]

9

(1)

\[\begin{aligned} &xf'(x)=f(x)+\frac{3a}{2}x^2 \\ &\left(\frac{f(x)}{x}\right)'=\frac{3a}{2} \\ &f(x)=(\frac{3a}{2}x+C)x=\frac{3a}{2}x^2+Cx \\ &2=\int_0^1f(x)dx=\left(\frac{a}{2}x^3+\frac{Cx^2}{2}\right) \bigg|_0^1=\frac{a}{2}+\frac{C}{2} \Rightarrow C=4-a \\ &f(x)=\frac{3a}{2}x^2+(4-a)x \end{aligned} \]

(2)

求得 \(a\) 得范围为：

\[\begin{aligned} &\begin{cases} f(1) \ge 0 \Rightarrow \frac{3a}{2}+4-a \ge 0 \Rightarrow a \ge -8 \\ f'(0) \ge 0 \Rightarrow 4-a \ge 0 \Rightarrow a \le 4 \end{cases} \\ &\Rightarrow -8 \le a \le 4 \end{aligned} \]

求得体积表达式：

\[\begin{aligned} V=&\pi \int_0^{1} f(x)^2 dx \\ =&\pi \int_0^1 \left( \frac{9a^2}{4}x^4+3a(4-a)x^3+(4-a)^2x^2 \right)dx \\ =&\pi \left( \left( \frac{9a^2}{20}x^5+ \frac{3a(4-a)}{4}x^4+\frac{(4-a)^2}{3}x^3 \right)\bigg|_0^1\right) \\ =&\pi \left(\frac{9a^2}{20}+\frac{-3a^2+12a}{4}+\frac{a^2-8a+16}{3} \right) \\ \end{aligned} \]

求导得：

\[V'(a)=\frac{9a}{10}+\frac{-6a+12}{4}+\frac{2a-8}{3}=\frac{54a-90a+180+40a-160}{60}=\frac{a+5}{15} \]

所以 \(a=-5\)

10

(1)

考虑点 \((r,\theta)\)

\[\begin{aligned} &\begin{aligned} dS=& \frac{1}{2} (r+dr)^2d\theta -\frac{1}{2}r^2d\theta \\ =&(rdr+\frac{(dr)^2}{2})d\theta \\ =&(rdr+o(dr))d\theta \\ \end{aligned} \\ &\begin{aligned} dV=& \int_0^{r}2\pi r\sin \theta dS \\ =&\int_0^{r(\theta)} \left(2\pi r^2 \sin \theta dr d\theta +\frac{(dr)^2}{2}d\theta \right) \\ =& 2\pi \sin \theta d\theta \int_0^{r(\theta)}r^2 dr \\ =& \frac{2\pi}{3} r^3(\theta) \sin \theta d\theta \\ \end{aligned} \\ &\begin{aligned} V=&\int_\alpha^{\beta} dV \\ =&\int_\alpha^\beta\frac{2\pi}{3} r^3(\theta) \sin \theta d\theta \end{aligned} \end{aligned} \]

(2)

\[\begin{aligned} V =&\int_{0}^{\pi}\frac{2\pi}{3} a^3(1+\cos \theta)^3\sin \theta d\theta \\ =&-\frac{2\pi}{3} a^3\int_0^\pi (1+\cos \theta)^3d\cos \theta \\ =&-\frac{2\pi}{3} a^3\int_1^{-1} (1+x)^3dx \\ =&\frac{2\pi}{3} a^3\int_{-1}^{1} (1+x)^3dx \\ =&\frac{2\pi}{3} a^3 \frac{(1+x)^4}{4} \bigg|_{-1}^1 \\ =&\frac{2\pi}{3} a^3 (4-0) \\ =&\frac{8\pi}{3} a^3 \end{aligned} \]