微积分(A)随缘一题[16]

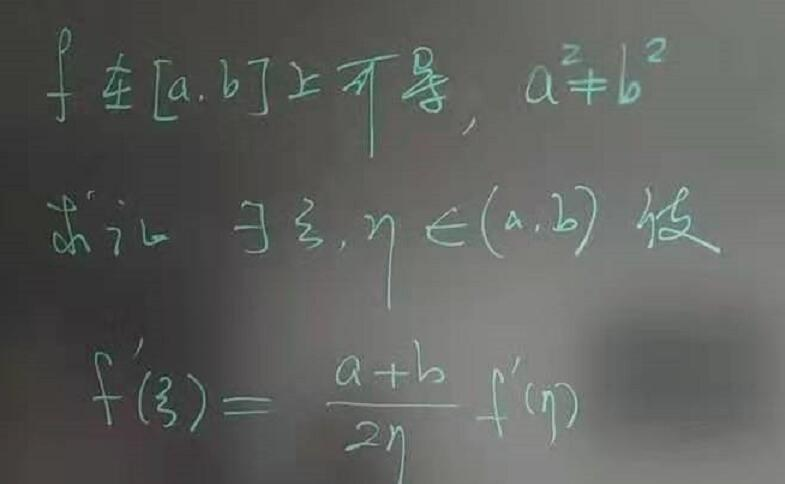
显然可以令 \(\zeta=\mu=\frac{a+b}{2}\)，此时满足题意（套路与反套路……）

---

考虑拉格朗日中值定理：

\[\exists \zeta \in (a,b),s.t. f(b)-f(a)=(b-a)f'(\zeta) \\ f'(\zeta)=\frac{a+b}{2} \frac{f'(\mu)}{\mu} \]

即：

\[\frac{f(b)-f(a)}{b-a} \frac{2}{a+b}=\frac{f'(\mu)}{\mu} \\ \frac{f'(\mu)}{2\mu}=\frac{f(b)-f(a)}{b^2-a^2} \]

考虑柯西中值定理：

\[\exists \mu \in (a,b),s.t.\frac{f(b)-f(a)}{b^2-a^2}=\frac{f'(\mu)}{2 \mu} \]

得证