微积分(A)随缘一题[11]

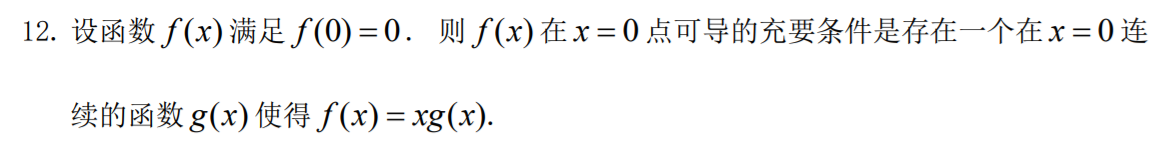
充分性

若 \(f(x)\) 在 \(x=0\) 处可导，则 \(f(x)\) 在 \(x=0\) 处连续

所以 \(g(x)=\frac{f(x)}{x}\) 在 \(x=0\) 处连续

必要性

若 \(g(x)=\frac{f(x)}{x}\) 在 \(x=0\) 处连续，则 \(\lim_{x \to 0} \frac{f(x)}{x}=g(0)\)

所以 \(f'(0)=\sum_{x \to 0}\frac{f(x)}{x}=g(0)\)，即 \(f(x)\) 在 \(x=0\) 处可导