10.27

t1

题意

给定一个有向图，含 $n$ 个顶点、$2n$ 条边，且每个顶点恰有 $2$ 条入边和 $2$ 条出边。从中删去 $n$ 条边，使每个顶点恰剩 $1$ 条入边和 $1$ 条出边。求满足条件的删边方案数，对 $998244353$ 取模。

对于所有数据，满足 $1 \leq n \leq 10^5$。

题解

假设一个点的两条出边为 $i , j $, 我们新建一个图给 $i , j$ 连边。如果一个点的两条入边为 $i , j $, 我们也给 $i , j$ 连边。

不难发现新图上每个点度数恰好为二，并且只有偶环。我们的要求事实上就是在新图上选几个不相邻的点，所以一个环就只有两种选法，于是答案显然是 $2^{\text{环数}}$ ，直接并查集即可。

t2

比赛过了但是原题没过，数据有点水。

题面

拿到肯定想到倍增，考虑直接处理从下向上死 $2^k$ 能到达的点。套一个倍增就能预处理了。

考虑把一条链从 $lca$ 断开。先跳到 $lca$ 下死的最上方，中间还会留一点。

这个部分如果长度 $<k$ 就不用死了，否则答案就会 $+1$。

t3

板子题。

题意

给定无向图 $G = (V, E)$，其中 $V = \{1, 2, \ldots, n\}$。对每个顶点 $v$ 给定权值 $f_x(v)$ 和 $f_y(v)$。边 $(i, j) \in E$ 当且仅当 $|f_x(i) - f_x(j)| + |f_y(i) - f_y(j)| \leq d$。求 $G$ 的最大团的顶点数。最大团：点数尽可能多的完全图。

题解

先把 $f_x(i)$ 和 $f_y(i)$ 当成坐标，然后考虑曼哈顿距离转切比雪夫距离。

那其实就是找出一个 $k\times k$ 的矩形能包含最多的点。

那其实就是这道题了，用扫描线直接写。

t4

题面

题意

一个合法的整数数列 $\{a_n\}$ 需要满足：

$1\le a_i\le n$ 。
令 $p_i=\max\{a_k|1\le k\le i\}$ ，则 $p_i\le p_{i-1}+1$

对于所有 $t\in[1,n]$ ，求 $\sum_{a}cnt(a,t)^2$ ，其中 $cnt(a,t)$ 表示 $t$ 在一个合法数列 $a$ 中的出现次数。

题解

首先有个套路，$cnt(a,t)^2$ 可以理解为 $t$ 在 $a$ 中可重复的选择两次。

根据上面的要求，我们可以定义一个 $f_{i,j}$ 表示前 $i$ 个中，$p_i=j$ 的方案数。

类似的定义一个 $g_{i,j}$ 表示倒着放 $i+1$ 个，且倒数第 $i+1$ 个 $p$ 为 $j$ 的方案数。

不难得出转移：

\[f_{i,j}=j\cdot f_{i-1,j}+f_{i-1,j-1}\\ g_{i,j}=j\cdot g_{i-1,j}+g_{i-1,j+1} \]

为了避免重复，我们枚举 $t$ 在 $a$ 中的第一次出现的位置 $i$ ，那么前 $i-1$ 位的方案数就是 $f_{i-1,t-1}$ 。

由于 $i$ 位置已经确定放了 $t$ ，我们现在有 $4$ 种情况：

$f_{i-1,t-1}\cdot g_{n-i,t}$ ：两个 $t$ 都选 $i$ 。
$2(n-i)f_{i-1,t-1}\cdot g_{n-i-1,t}$ ：一个 $t$ 选 $i$ ，另一个 $t$ 不选 $i$ 。
$(n-i)f_{i-1,t-1}\cdot g_{n-i-1,t}$ ：两个 $t$ 都不选 $i$ ，且位置相同。
$2{n-i\choose 2}f_{i-1,t-1}\cdot g_{n-i-2,t}$ ：两个 $t$ 都不选 $i$ ，且位置不同。

由于 $i$ 位置开始已经有了 $t$ ，所以后面放 $t$ 是一定合法的，我们可以直接把后面放 $t$ 的位置无视掉。

补一下上周六比赛

t1

题面

看数据范围考虑区间 dp，发现不好合并，考虑枚举最后一步。

首先将 $a$ 和 $b$ 离散化，考虑区间 $\mathrm { d p } $, 设 $f _ { l , r }$ 表示修复 $\left[ a _ { i } , b _ { i } \right] \subseteq [ l , r ]$ 的所有故障所需的最少能量，由于必然有一次操作会涉及到距离最远的点，设 $D$ 表示范围内的所有 $i$ 的 $d _ { i }$ 的最大值，枚举在哪个时刻使用，设其为 $k $, 那么所有满足 $k \in \left[ a _ { i } , b _ { i } \right]$ 的故障都会被修复，只剩下没有跨越 $k$ 的故障，故有：

\[f _ { l , r } = \lim _ { k = l + 1 } ^ { r - 1 } \left\{ f _ { l , k - 1 } + f _ { k + 1 , r } \right\} + D \]

t2

原题

题意

给定一个 $n$ 个点 $m$ 条边的无向图，现在每条边可能是黑色或者白色，有 $2^m$ 种可能。

只保留所有黑边之后，如果整个图每个顶点的度数为偶数，那么这个图米奇很喜欢！

现在米奇想知道，所有米奇喜欢的染色方案里黑边数量的平方和。由于数字太大，只需要输出对 $10^9+7$ 取模的结果。

题解

考虑把平方和套路性拆开，拆成任选两个边都存在的方案数，那现在就要就出这个种类数了。

考虑对于每个连通块拎出来一个 $d f s$ 树，任意的决定所有非树边是黑的还是白的，所有树边的状态就可以唯一确定了。确定方式就是从下往上构造，如果这个点度数是奇数，就把这个点和父亲的边的染黑，否则白。注意到根的度数一定是偶数。因此方案数是 $2 ^ { m - n + c } $, 其中 $c$ 是连通块个数。

平方和可以枚举两个边算一下贡献。计算这两个为黑色有多少个染色方案是好的。

cas1:这两个边存在一个割边。假设第一个边是割边，图分成了两个连通块，考虑没有第二个边的连通块。这个连通块恰有一个点度数增加了 $1$，因此整个连通块的度数一定是奇数，所以一定无解。

case2:这两个边删掉之后，整个图的连通块个数增加了1，此时方案数是 $2 ^ { m - n + c - 1 } $。

case3:这两个边删掉之后，整个图的连通块个数不变，方案数是 $2 ^ { m - n + c - 2 } $。
因此我们只需要分别统计三类点对的个数。其中一个方法是：考虑 $d f s$ 树的每个非树边，给这个非树边和对应的树链上的边同时x0r一个随机数。

所有权值为 $0$ 的边是割边，权值相同的边属于 $c a s e 2 $, 剩余的属于 $c a s e 3 $。正确性证明可以百度 DZY loves Chinese II 用哈希表做到时间复杂度 $O ( n ) $。

t3

题面

考虑第一问，其实就是最短路。考虑第二问，对于每个点，其实有贡献的点就是在最短路 DAG 上的点。也就是满足 $dis_u+w=dis_v$ 的这些 $E=u\to v$。建了图之后我们发现一个方程 $dp_u=dp_v+(dis_u-dis_v)^2$。其中 $v$ 是 $u$ 的一级祖先的道路上 $dis$ 比 $u$ 小的节点。考虑拓扑处理，那现在就只需要维护出每个可达铁路的 $\max(dp_v+(dis_u-dis_v)^2)$ 了。这是一个经典的可以用斜率优化的式子，拆开用李超树维护即可。

t4

题面

这篇讲的挺好的：link

P8170

题面

考虑二分答案，然后性质就是贪心选择能操作的直接操作。考虑怎么快速找到能操作的，就是直接剪掉了把下一次操作的时间算出来放在对应时间的 vector 里面，时间复杂度 $O((n+m+k)\log V)\to O(mk\log v)$。

你也可以直接放堆里维护 $O(n\log V+k\log n\log V)$。

P3660

题面

$a$ 为左端点，$b$ 为右端点。

为了满足 $a_i\le a_j\le b_i\le b_j$ 容易发现是三维偏序，但是可以直接用树状数组。

先左端点从小到大排序 $a_j\le b_i\le b_j$，然后就是一个区间求和，单点修改把右端点放进去。

P1064

题面

我最开始以为依赖性背包还比较难，没想到就是分组背包，考虑这一组内只有 $4$ 种情况，直接背包做完了。

p3961

题面

还是依赖性背包，考虑按照斜率分组，然后这个依赖性的处理就是每个点的斜率前缀和算一个值，然后同一个斜率算一个组，然后直接背包就好了。

P3512

题面

做点水题，考虑双指针，做完了。

AT_abc150_d

题面

考虑拆贡献。拆成 $(1+2p)\times \frac{a_k}{2}$。然后就是关于 $\frac{a_k}{2}$ 的 $lcm$ 的倍数为奇数的个数，特判一下初始就是自己偶数倍的情况 $=0$ 就好了。

P5597

题面

考虑一个循环内机器要怎么动。他应该吧除终点子树的东西吃了吧，然后递归完成相同情况，那么完成的就是所有情况的树的并。然后来看怎么计算这棵树的答案，就是 $2(n-1)+d$ 其中 $d$ 为终点深度，$n$ 为节点个数，枚举每种终点，每次遍历这棵树。

P3006

题面

P8122

题面

复习一下函数交互。先看数据范围，估计是 $\log n +???$ 考虑分类讨论。接下来auther

分类讨论有没有选择 $\geq A$ 的数。如果选择了，一定是仅选择一个 $\geq A$ 中最小的数，这时已经满足 $\geq A$ 了，剩下的肯定是要取前 $k-1$ 小。

如果没有选择，那么先默认选择最小的 $k$ 个数，如果和 $<A$，就不断把最小的数换成 $<A$ 的数中最大的数，这样每次的变化量都小于 $A$，不会突然超过 $2A$ 的上界限制。

先找到第一个 $\geq A$ 的数的下标 $i$，还要知道下标在 $[1,k]$ 和 $[i-k,i-1]$ 中的数的值，总询问次数 $\log n+2k$。

P14234

题意

考虑只关注逆过来的边，就像这样。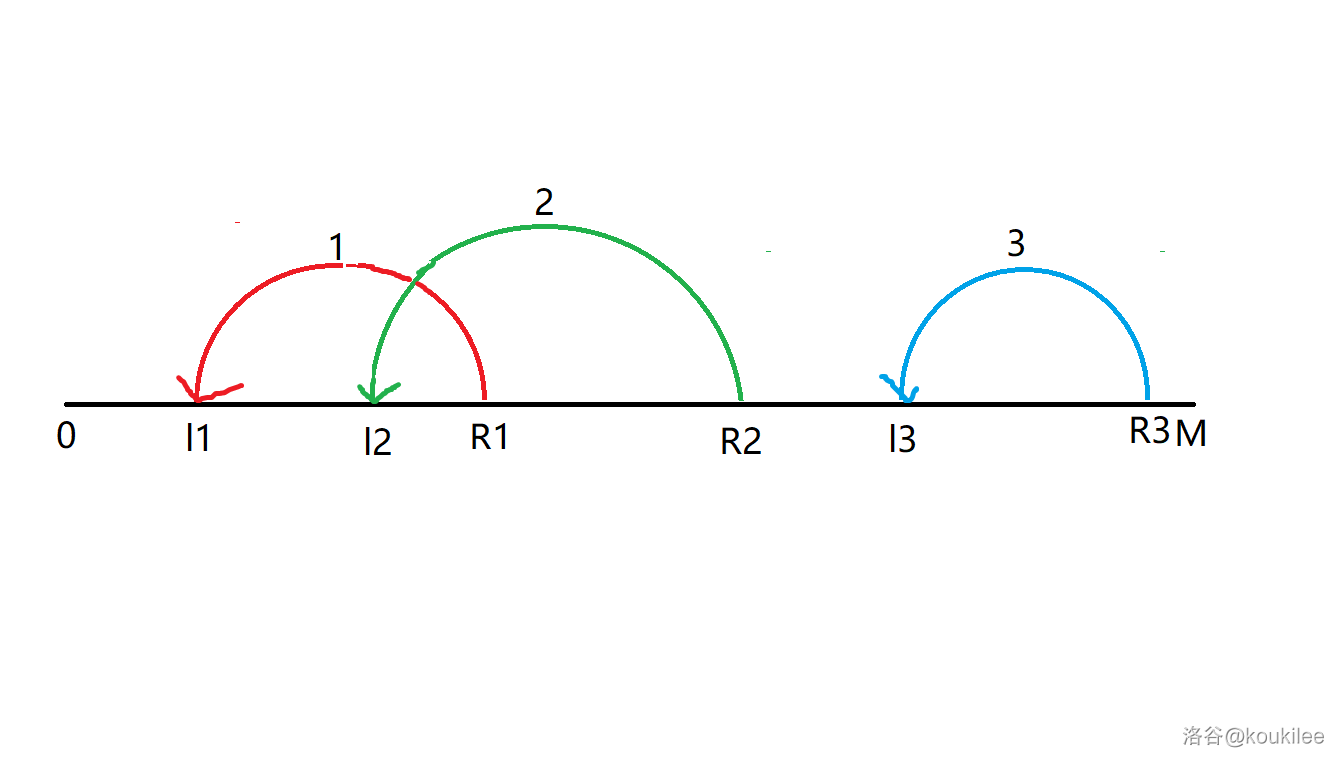

发现要最小化遍历所有边的长度，其实就是要求这些边的长度并，我们有个结论：

求若干条线段的交的长度，按照左端点排序一下贪心右端点即可。

证明用手模即可。

还有一种做法：我们考虑对左右端点都分别排序，然后排序后的 $x_i,y_i$ 代表的区间并也是原来的区间并。

但是现在保证了左右端点递增，所以总长度就是：

for(int i=1;i<=cnt;i++){
	ans+=2*(x[i]-max(x[i-1],y[i]));
}

P3076

顺便回忆一下一道类似的题

题面

和刚才不一样的就是这一次每趟只能带一个人。考虑设起始点，终点分别为 $st_i,ed_i$.

那答案就是排序找到一种序列最小化 $\sum_{i=1}^{n}|st_i-ed_i|+|ed_i-st_j|$。

第一段是定值，考虑最小化第二段。对于第二段，我们有经典结论，就是：

把 $ed$ 和 $st$ 数组从小到大排序 $ans=\sum_{i=1}^{n}|st_i-ed_i|$。

证明就是任意交换一定不优，交叉部分一定不减。

posted @ 2025-10-27 21:53 NeeDna 阅读(9) 评论(0) 收藏举报

刷新页面返回顶部

needna