浅析梯度下降算法
线性回归
首先对于若干数据点,每一个数据点\(\bm{x}\in\mathbb{R}^N\),我们用超平面\(b+\sum_{n=1}^Nx_n\theta_n\bm{i}_n=0\)对其进行划分。这时需要向量\(\bm\theta\in\mathbb{R}^N\),我们让截距\(b\)也成为一个参数,让下标\(n\)从0计,这样上式可以写成\(\bm\theta^\textsf{T}\bm{x}=0\)其中\(x_0=1\)。
我们有线性回归一般公式:\(\displaystyle f_{\bm\theta}(\bm{x})=\sum_{n=0}^Nx_n\theta_n\);我们令\(\hat{y}=f_{\bm\theta}(\bm{x})\)。
损失函数
现在已经对\(I\)个数据点求解了线性回归,然后求出损失:
- L1损失:\(\displaystyle J=\frac{1}{I}\sum_{i=1}^I\big\lvert {\hat{y}^{(i)}-y^{(i)}}\big\rvert\);
- L2损失:\(\displaystyle J=\frac{1}{I}\sum_{i=1}^{I}{\big({\hat{y}^{(i)}-y^{(i)}}\big)}^2\),L2损失看上去就是求出来实际值\(y\)与预测值\(\hat{y}\)之间距离平方之和;
- 交叉熵:\(\displaystyle J=-\frac{1}{I} \sum_{i=1}^I \big(y^{(i)} \ln{ \hat{y}^{(i)}+ (1-y^{(i)}) } \ln{ (1- \hat{y}^{(i)} )} \big)\)。
梯度下降
我们知道,梯度表示某一函数在一点处的方向导数,\(\nabla_\bm\theta\),沿着其方向取得级大值,那么梯度下降就可以获得我们想要的极小值。但是梯度下降不能一次性到达极小值,而是需要每轮迭代步进到极小值,而步进总有个步长,这个步长可以用学习率\(Lr\)和上面求出来的损失\(J\)表示。超平面的参数\(\bm\theta\)本身也是\(N\)维空间中一点,每次将它的坐标加上\(Lr\nabla_\bm\theta J\),当\(\bm\theta\)坐标不再移动时,点\(\bm\theta\)基本上就是极小值点。
现在看看采用不同损失函数时梯度下降如何更新将参数\(\bm\theta\):
- L1损失:
\(\begin{aligned}\bm\theta^\prime &= \bm\theta-Lr\nabla_\bm\theta J\\&= \bm\theta-Lr\frac{\partial J}{\partial\bm\theta}\\&= \bm\theta-Lr\sum_{n=0}^N\bigg(\frac{\partial\big(\frac{1}{I}\sum_{i=1}^I\lvert\theta_nx_n^{(i)}-y^{(i)}\lvert\big)}{\partial\theta_n}\bigg)\\&= \bm\theta-Lr\frac{1}{I}\sum_{n=0}^N\sum_{i=1}^I{\left\{\begin{aligned}\theta_nx_n^{(i)}-y^{(i)},\quad& \theta_nx_n^{(i)}-y^{(i)}\geq 0 \\y^{(i)}-\theta_nx_n^{(i)},\quad& \theta_nx_n^{(i)}-y^{(i)}< 0\end{aligned}\right.}\\&= \bm\theta-Lr\sum_{i=1}^I\lvert\hat{y}^{(i)}-y^{(i)}\rvert\end{aligned}\) - L2损失:
\(\begin{aligned}\bm\theta^\prime &= \bm\theta-Lr\nabla_\bm\theta J\\&= \bm\theta-Lr\frac{\partial J}{\partial\bm\theta}\\&= \bm\theta-Lr\sum_{n=0}^N\bigg(\frac{\partial\big(\frac{1}{I}\sum_{i=1}^I(\theta_nx_n^{(i)}-y^{(i)})^2\big)}{\partial\theta_n}\bigg)\\&= \bm\theta-Lr\sum_{n=0}^N\bigg(\frac{1}{2I}\sum_{i=1}^I\Big(\theta_nx_n^{(i)}-y^{(i)}\Big)x_n^{(i)}\bigg)\\&= \bm\theta-Lr\sum_{i=1}^I\Big((\hat{y}^{(i)}-y^{(i)})\bm{x}^{(i)}\Big)\end{aligned}\) - 交叉熵:
输出:import sympy x, y, t = sympy.symbols('x y t') print(sympy.diff(y*sympy.log(x*t)+(1-y)*sympy.log((1-(x*t))), t)) # 对交叉熵关于参数t(即θ)求导
所以:\(\displaystyle\bm\theta^\prime= \bm\theta-Lr\sum_{i=1}^I\Big(\big(\frac{y^{(i)}}{\hat{y}^{(i)}}+\frac{1-y^{(i)}}{1-\hat{y}^{(i)}}\big)\bm{x}^{(i)}\Big)\)-x*(1 - y)/(-t*x + 1) + y/t
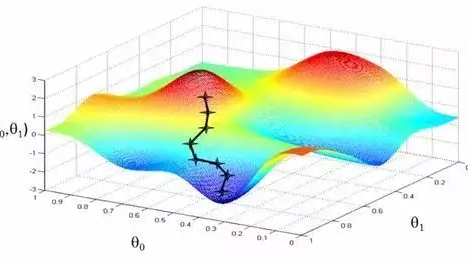 我们知道,梯度表示某一函数在一点处的方向导数,$\nabla_\bm\theta$,沿着其方向取得级大值,那么梯度下降就可以获得我们想要的极小值。但是梯度下降不能一次性到达极小值,而是需要每轮迭代步进到极小值,而步进总有个步长,这个步长可以用学习率$Lr$和上面求出来的损失$J$表示。超平面的参数$\bm\theta$本身也是$N$维空间中一点,每次将它的坐标加上$Lr\nabla_\bm\theta J$,当$\bm\theta$坐标不再移动时,点$\bm\theta$基本上就是极小值点。
我们知道,梯度表示某一函数在一点处的方向导数,$\nabla_\bm\theta$,沿着其方向取得级大值,那么梯度下降就可以获得我们想要的极小值。但是梯度下降不能一次性到达极小值,而是需要每轮迭代步进到极小值,而步进总有个步长,这个步长可以用学习率$Lr$和上面求出来的损失$J$表示。超平面的参数$\bm\theta$本身也是$N$维空间中一点,每次将它的坐标加上$Lr\nabla_\bm\theta J$,当$\bm\theta$坐标不再移动时,点$\bm\theta$基本上就是极小值点。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号