Leetcode 167. 两数之和 II - 输入有序数组&&一张图告诉你 O(n) 的双指针解法的本质原理
&&一张图告诉你 O(n) 的双指针解法的本质原理
简单
给定一个已按照 非递减顺序排列 的整数数组 numbers ,请你从数组中找出两个数满足相加之和等于目标数 target 。
函数应该以长度为 2 的整数数组的形式返回这两个数的下标值。numbers 的下标 从 1 开始计数 ,所以答案数组应当满足 1 <= answer[0] < answer[1] <= numbers.length 。
你可以假设每个输入 只对应唯一的答案 ,而且你 不可以 重复使用相同的元素。
示例 1:
输入:numbers = [2,7,11,15], target = 9 输出:[1,2] 解释:2 与 7 之和等于目标数 9 。因此 index1 = 1, index2 = 2 。 示例 2:
输入:numbers = [2,3,4], target = 6 输出:[1,3] 示例 3:
输入:numbers = [-1,0], target = -1 输出:[1,2]
提示:
2 <= numbers.length <= 3 * 104 -1000 <= numbers[i] <= 1000 numbers 按 非递减顺序 排列 -1000 <= target <= 1000 仅存在一个有效答案
代码如下
static int[] twoSum(int[] nums, int target) {
int left = 0;
int right = nums.length - 1;
while (left < right) {
int sum = nums[left] + nums[right];
if (sum == target) {
return new int[]{left + 1, right + 1};
} else if (sum > target) {
right--;
} else {
left++;
}
}
return new int[]{};
}
作者:nettee
很多人做这个题目想不到正确的 O(n)O(n) 解法,即使看了答案理解了,下次再做的时候还是会忘记。要想真正理解这道题,就要明白解法背后的道理。这样不仅可以记住这道题,还能举一反三解决类似的题目。
需要注意的是,虽然本题叫做 Two Sum II,但解法和 Two Sum 完全不同。
图解双指针解法的原理 在这道题中,我们要寻找的是符合条件的一对下标 (i, j)(i,j),它们需要满足的约束条件是:
-
ii、jj 都是合法的下标,即 0 \le i < n, 0 \le j < n0≤i<n,0≤j<n
-
i < ji<j(题目要求)
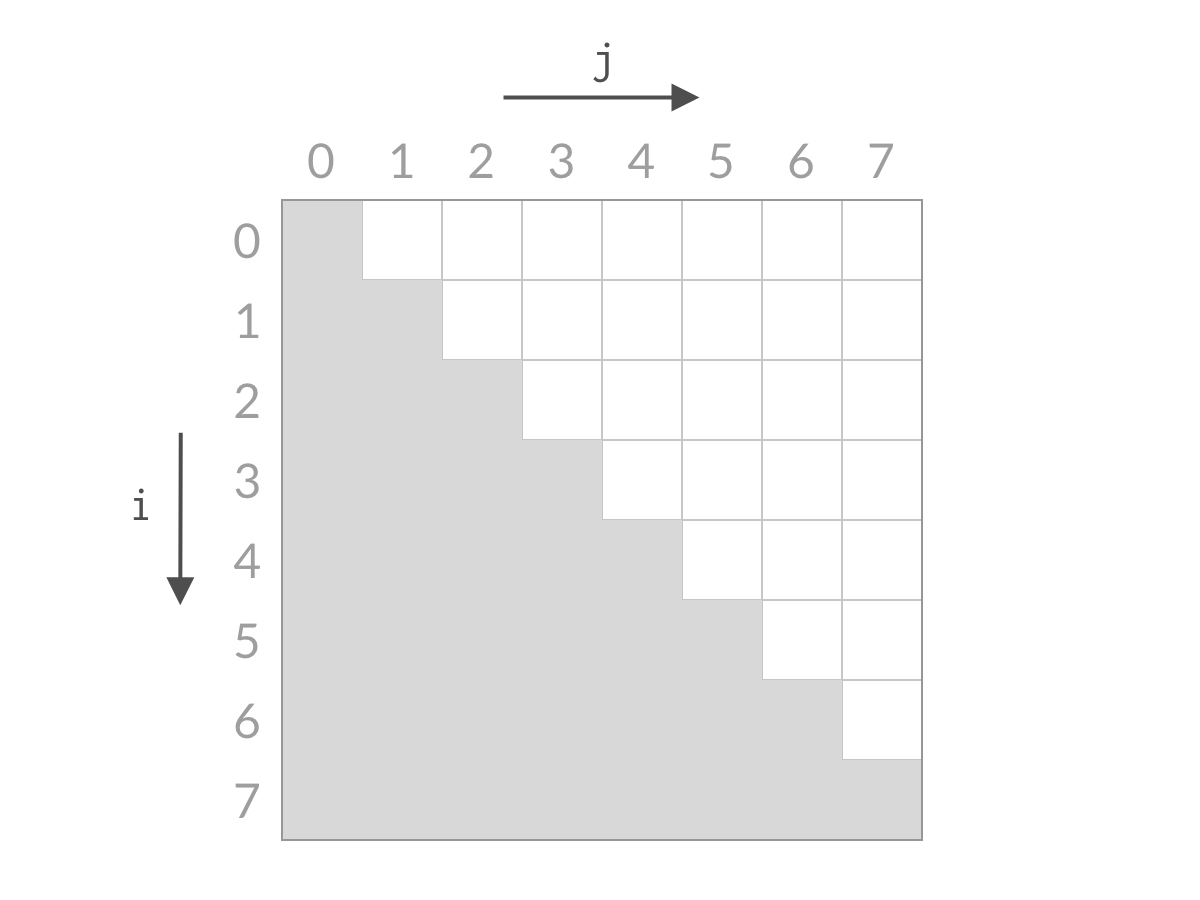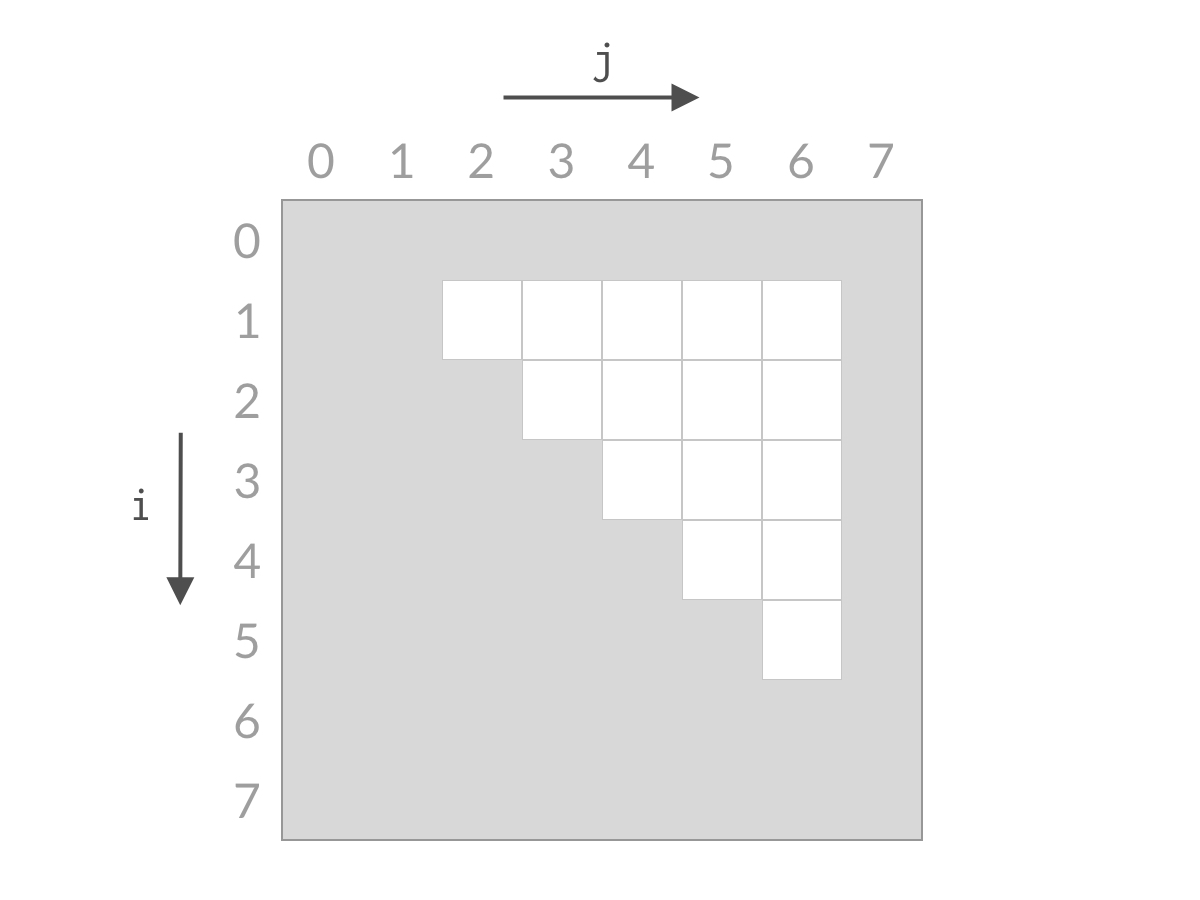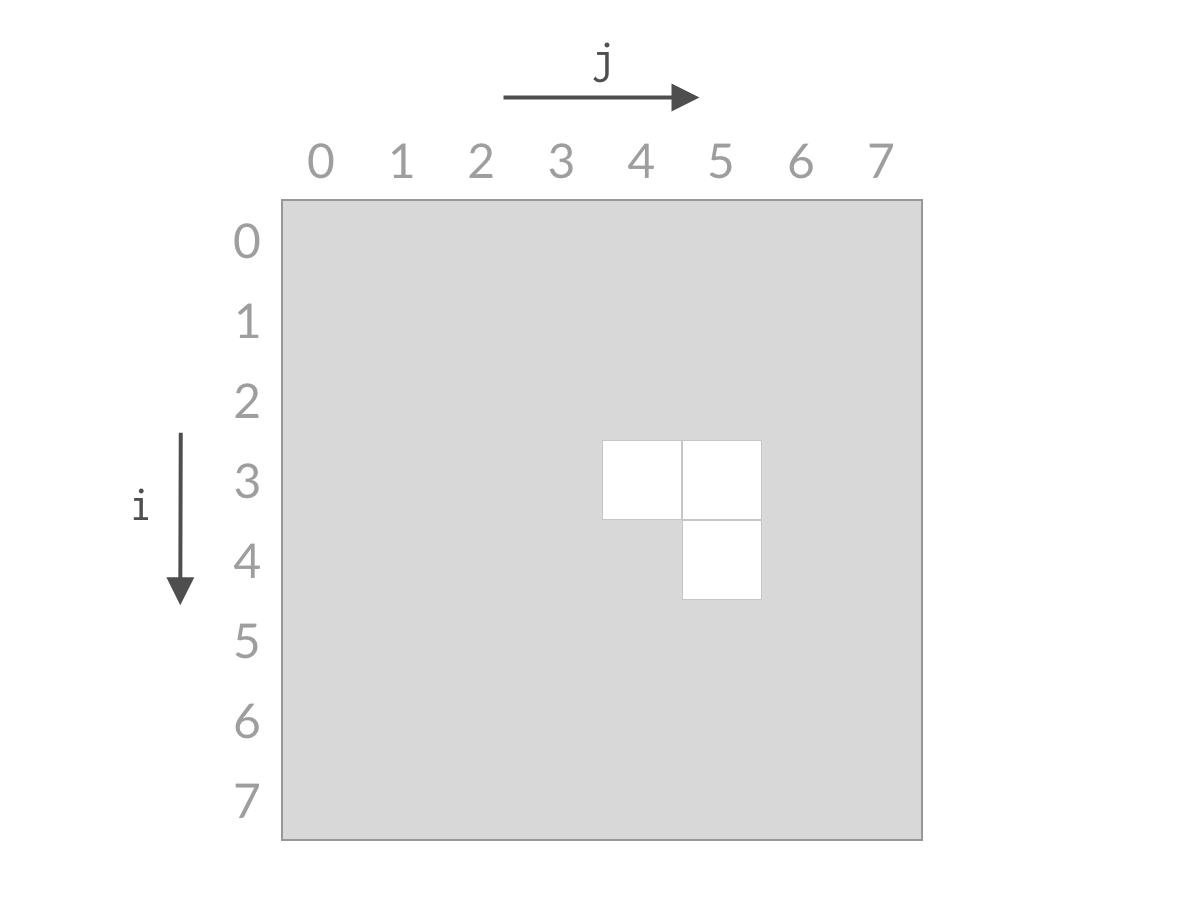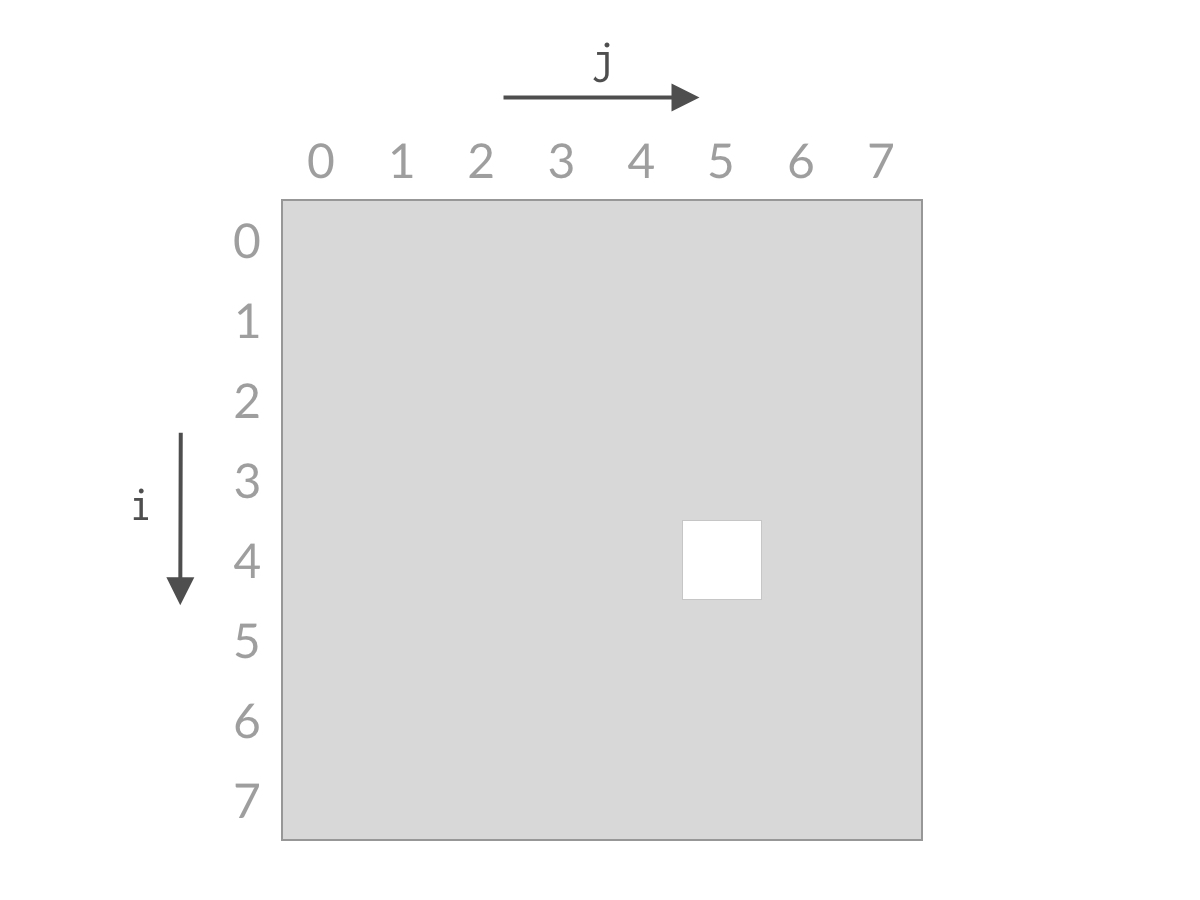
而我们希望从中找到满足 A[i] + A[j] == target 的下标 (i, j)(i,j)。以 n = 8n=8 为例,这时候全部的搜索空间是:
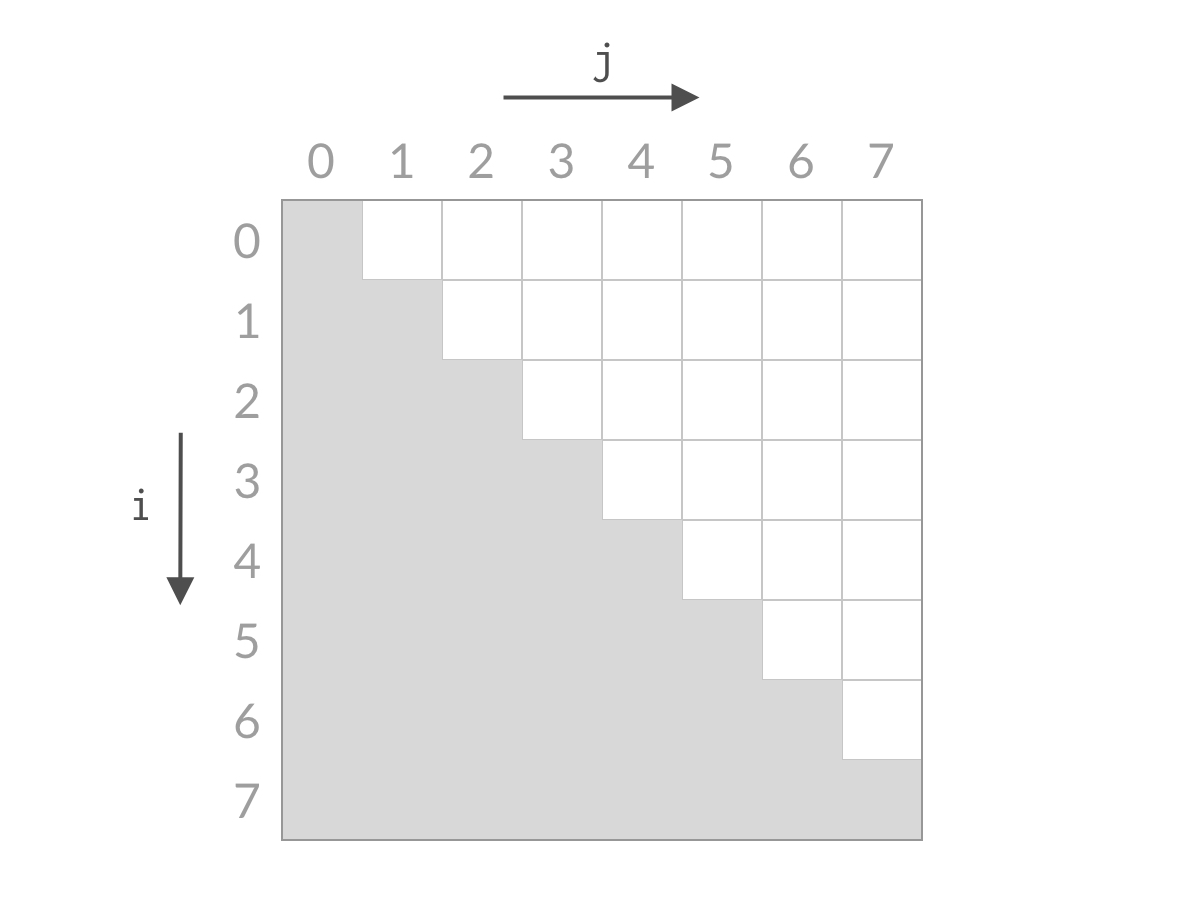
由于 ii、jj 的约束条件的限制,搜索空间是白色的倒三角部分。可以看到,搜索空间的大小是 O(n^2)O(n 2 ) 数量级的。如果用暴力解法求解,一次只检查一个单元格,那么时间复杂度一定是 O(n^2)O(n 2 )。要想得到 O(n)O(n) 的解法,我们就需要能够一次排除多个单元格。那么我们来看看,本题的双指针解法是如何削减搜索空间的:
一开始,我们检查右上方单元格 (0, 7)(0,7),即计算 A[0] + A[7] ,与 target 进行比较。如果不相等的话,则要么大于 target,要么小于 target。
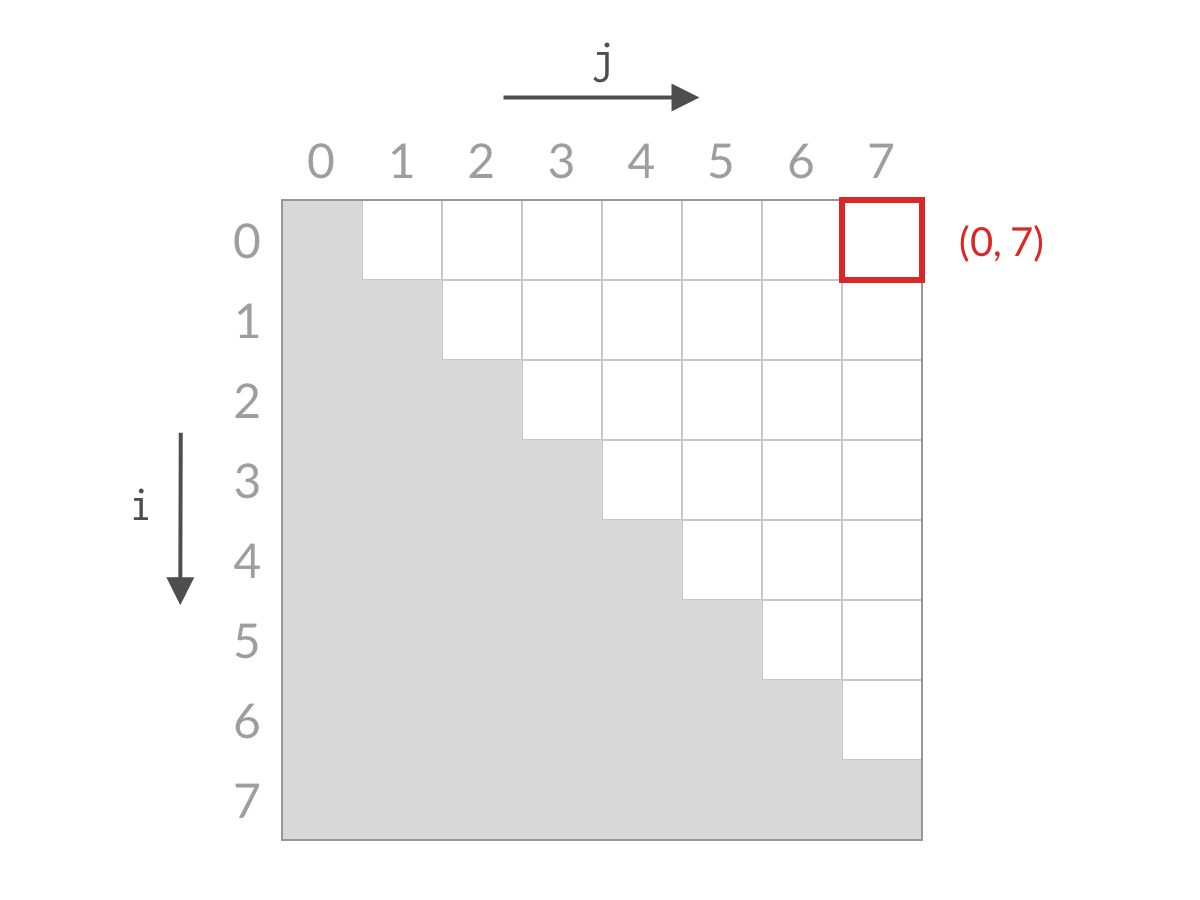
假设此时 A[0] + A[7] 小于 target。这时候,我们应该去找和更大的两个数。由于 A[7] 已经是最大的数了,其他的数跟 A[0] 相加,和只会更小。也就是说 A[0] + A[6] 、A[0] + A[5]、……、A[0] + A[1] 也都小于 target,这些都是不合要求的解,可以一次排除。这相当于 i=0i=0 的情况全部被排除。对应用双指针解法的代码,就是 i++,对应于搜索空间,就是削减了一行的搜索空间,如下图所示。
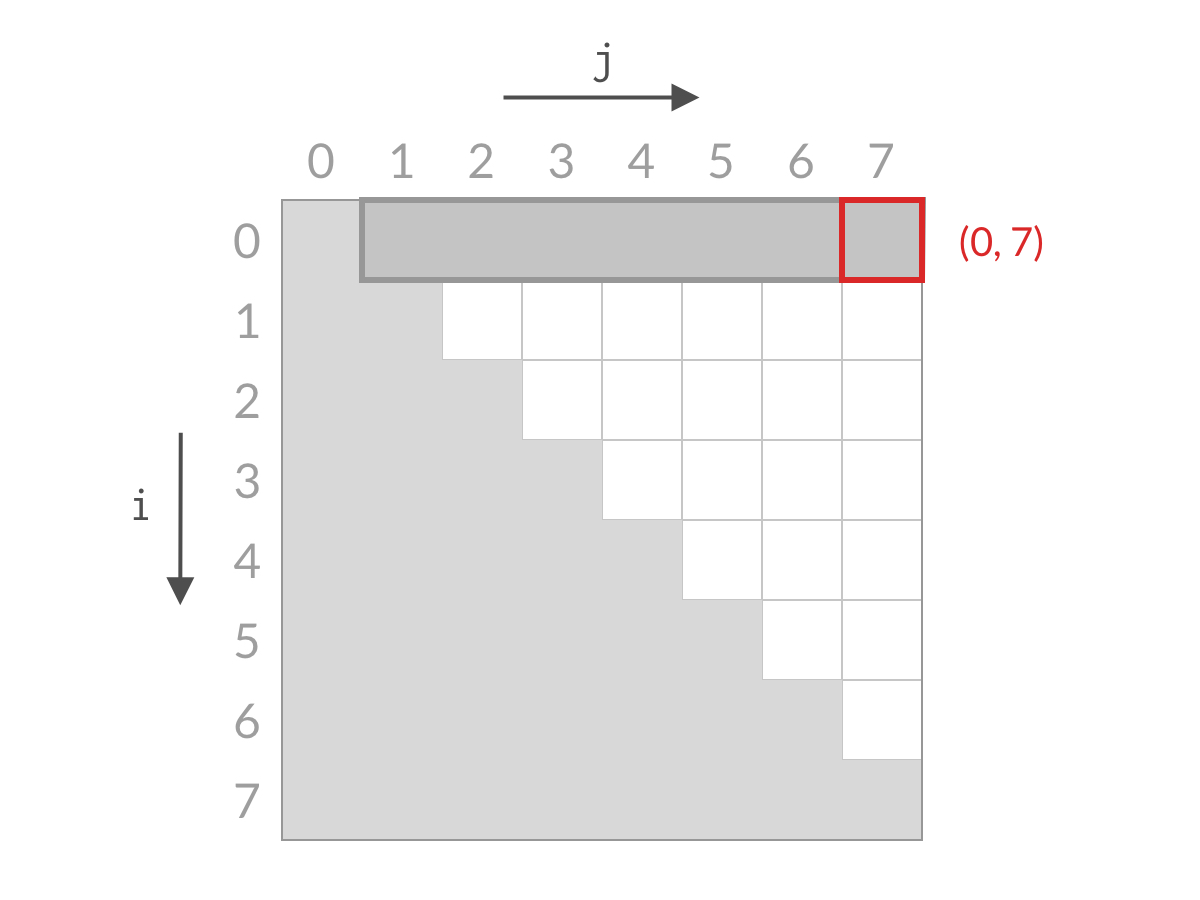
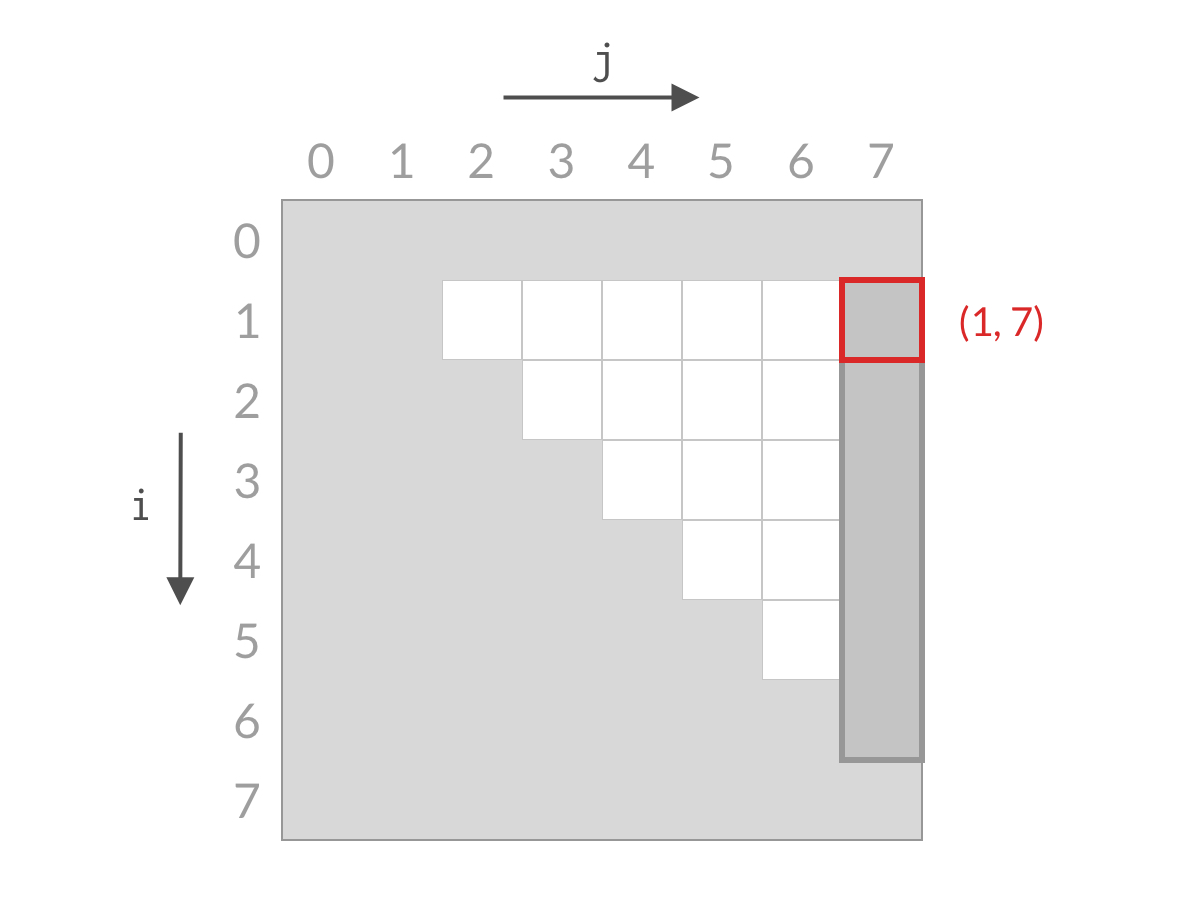
排除掉了搜索空间中的一行之后,我们再看剩余的搜索空间,仍然是倒三角形状。我们检查右上方的单元格 (1, 7)(1,7),计算 A[1] + A[7] 与 target 进行比较。
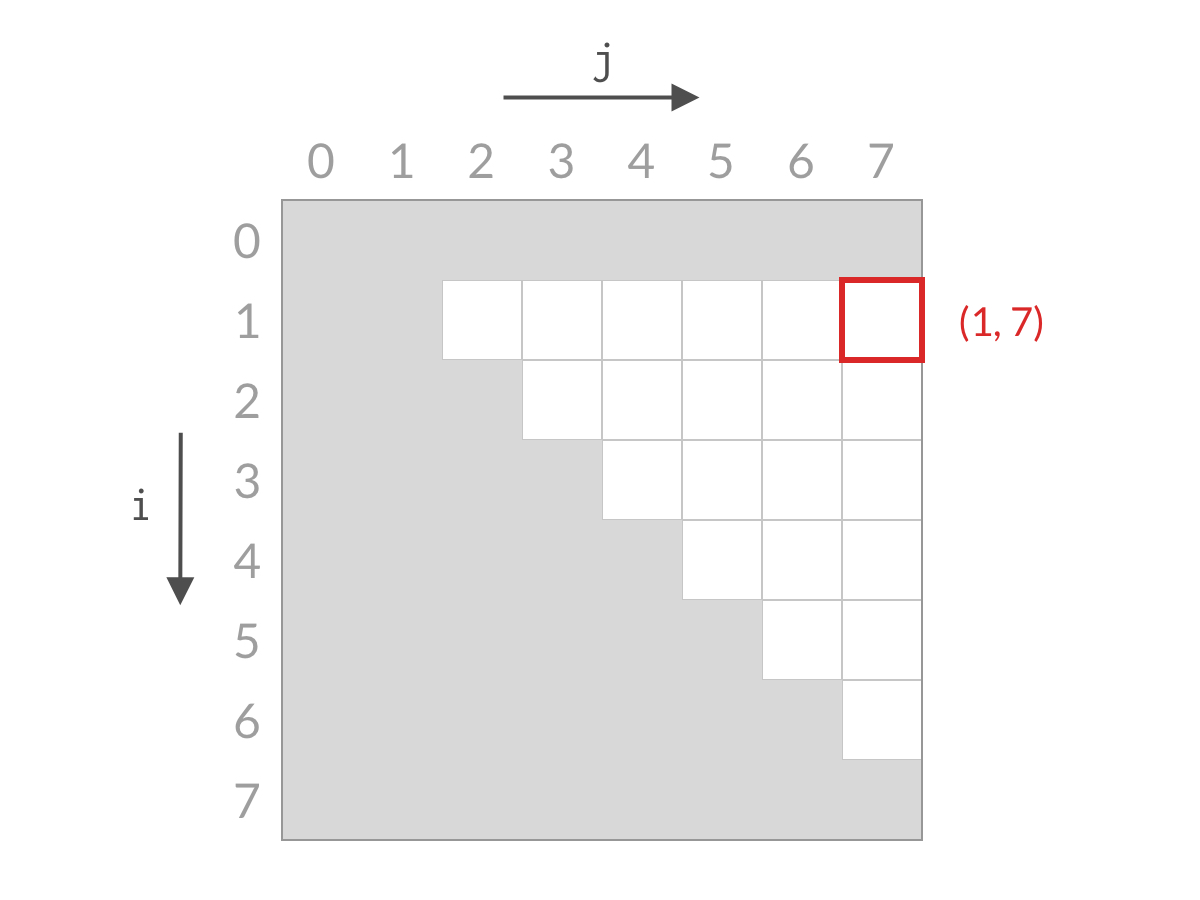
假设此时 A[0] + A[7] 大于 target。这时候,我们应该去找和更小的两个数。由于 A[1] 已经是当前搜索空间最小的数了,其他的数跟 A[7] 相加的话,和只会更大。也就是说 A[1] + A[7] 、A[2] + A[7]、……、A[6] + A[7] 也都大于 target,这些都是不合要求的解,可以一次排除。这相当于 j=0j=0 的情况全部被排除。对应用双指针解法的代码,就是 j++,对应于搜索空间,就是削减了一列的搜索空间,如下图所示。
可以看到,无论 A[i] + A[j] 的结果是大了还是小了,我们都可以排除掉一行或者一列的搜索空间。经过 nn 步以后,就能排除所有的搜索空间,检查完所有的可能性。搜索空间的减小过程如下面动图所示:
实际上还有几道题也是用到了这样的缩减搜索空间的思想:


 浙公网安备 33010602011771号
浙公网安备 33010602011771号