拟合线性模型

R 中最简单的模型就是线性模型，即使用一个线性模型描述两个随机变量在一系列假
设下的关系。在以下例子中，我们创建了一个线性函数，将 x 映射到 3+2*x（即 f(x)）。
然后，生成一个正态分布的随机数值向量 x，再用 f(x)加上一些独立的噪声生成 y：
f <- function(x) 3 +2 * x
x <- rnorm(100)
y <- f(x) +0.5 * rnorm(100)

假设不知道 y 是如何通过 x 生成的，那么我们还能用线性模型还原它们之间的关系，
即还原线性模型的系数吗？以下代码中，lm( )用线性模型拟合 x 和 y 的关系。需要注意
的是 y~x 表达式告诉 lm( )这个线性回归是关于因变量 y 和单个回归元（regressor）x 的：
model1 <- lm(y ~x)
model1
##
## Call:
## lm(formula = y ~ x)
##
## Coefficients:
## (Intercept) x
## 2.969 1.972
真实模型的系数是 3（截距）和 2（斜率），用样本数据 x 和 y 拟合的模型系数为
2.9692146（截距）和 1.9716588（斜率），这和模型的真实系数非常接近。
我们将模型保存为 model1。要得到模型的系数，可以用以下代码：
coef(model1)
## (Intercept) x
## 2.969215 1.971659
也可以用 model1$查看模型的系数，因为 model1 本质上是一个列表。
此外，还可以调用 summary( )了解更多关于这个线型模型的统计性质：
summary(model1)
##
## Call:
## lm(formula = y ~ x)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.96258 -0.31646 -0.04893 0.34962 1.08491
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 2.96921 0.04782 62.1 <2e-16 ***
## x 1.97166 0.05216 37.8 <2e-16 ***
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

##
## Residual standard error: 0.476 on 98 degrees of freedom
## Multiple R-squared: 0.9358, Adjusted R-squared: 0.9352
## F-statistic: 1429 on 1 and 98 DF, p-value: < 2.2e-16
要理解以上统计内容，最好回顾一两本统计学教材的线性回归章节。图 7-31 将数据和
拟合模型放到了一起：
plot(x, y, main = "A simple linear regression")
abline(coef(model1), col = "blue")

 

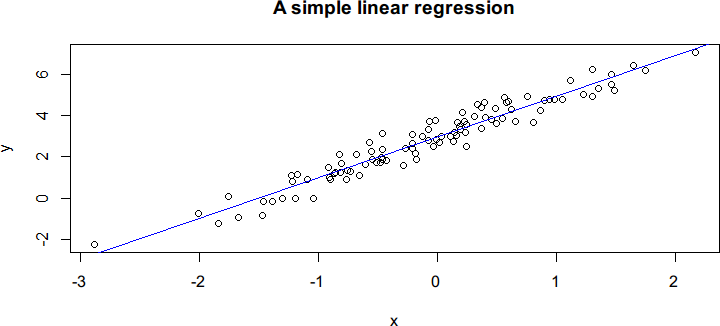
图 7-31
在上述代码中，我们直接为 abline( )提供包含回归系数估计的两元素数值向量，
用来添加拟合的回归线。
接下来，我们可以调用 predict( )对所拟合模型进行预测。在一个标准误差下，预
测 x=-1 和 x=0.5 时的 y，运行以下代码：
predict(model1, list(x = c(-1, 0.5)), se.fit = TRUE)
## $fit
## 1 2
## 0.9975559 3.9550440
##
## $se.fit
## 1 2
## 0.06730363 0.05661319
##
## $df
## [1] 98
##
## $residual.scale
## [1] 0.4759621

预测结果是一个列表，其中包含了 y 的预测值（$fit）、拟合值的标准误差（$se.fit）、
自由度（$df）和残差标准差（$residual.scale）。
现在，我们已经基本上学会了如何对给定数据拟合线性模型，接下来就看一些现实生
活中的数据。下面的例子中，我们试着用不同复杂度的线性模型预测航班的飞行时间。其
中，对于预测飞行时间最为显著的变量是飞行距离。
首先，我们加载数据集并绘制飞行距离和飞行时间 air_time 的散点图。因为数据集
的记录条数非常多，我们用 pch="." 使每个数据点变得非常小：
data("flights", package = "nycflights13")
plot(air_time ~distance, data = flights,
pch = ".",
main = "flight speed plot")
图 7-32 清楚地表明飞行距离和飞行时间之间有正向相关关系，因此用线性模型拟合这
两个变量是合理的。

 

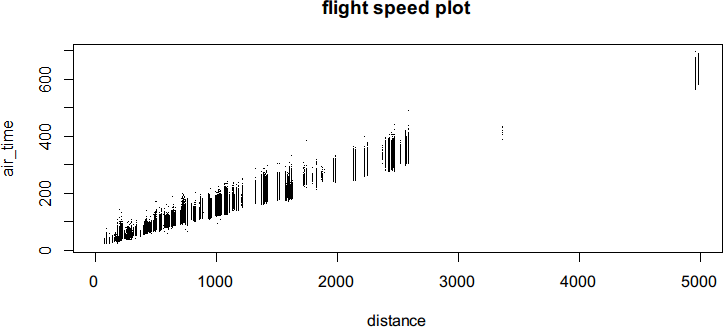
图 7-32
在将整个数据集输入线性模型之前，我们将数据集分成两部分：训练集和测试集。划分
测试集的目的是我们不仅想要进行模型的样本内评估，还要进行样本外评估。更具体地说，
我们把 75%的数据放入训练集，把剩下 25%的数据放入测试集。在以下代码中，sample( )
取出原始数据记录 75%的随机样本，并用 setdiff( )得到剩下的数据记录：
rows <- nrow(flights)
rows_id <- 1:rows
sample_id <- sample(rows_id, rows * 0.75, replace = FALSE)
flights_train <- flights[sample_id,]
flights_test <- flights[setdiff (rows_id, sample_id), ]
注意，setdiff(rows_id, sample_id)返回的是 rows_id 的索引而不是 sample_id

的索引。
现在，flights_train 是训练集，flights_test 是测试集。使用划分好的数据集，
模型的拟合和评估流程就很简单了。首先，我们使用训练集拟合模型，然后做一个样本内
预测来看样本内误差的大小：
model2 <- lm(air_time ~distance, data = flights_train)
predict2_train <- predict(model2, flights_train)
error2_train <- flights_train$air_time -predict2_train
为了计算误差的大小，我们定义一个 evaluate_error( )函数计算平均绝对误差和
误差的标准差：
evaluate_error <- function(x) {
c(abs_err = mean(abs(x), na.rm = TRUE),
std_dev = sd(x, na.rm = TRUE))
}
用这个函数，我们可以计算模型 model2 的样本内预测误差：
evaluate_ _error(error2_train)
## abs_err std_dev
## 9.413836 12.763126
平均绝对误差表示平均来看预测值偏离真实值的绝对值约为 9.41 分钟，且误差的标准
差为 12.8。
接下来，我们用模型对测试集进行预测，做一个简单的样本外评估：
predict2_test <- predict (model2, flights_test)
error2_test <- flights_test$air_time -predict2_test
evaluate_ _error(error2_test)
## abs_err std_dev
## 9.482135 12.838225
预测结果被保存在一个含预测值的数值向量中。平均绝对误差和误差的标准差都有轻
微的上升，表明样本外预测的质量没有明显地变差，看来 model2 没有过拟合。
因为 model2 只有一个回归元——路程（distance），很自然地就会想到包含更多回归
元是否会提高模型的预测效果。以下代码拟合一个新的线性模型，它不仅包含路程，还包
含航空公司（carrier）、月份（month）和起飞时间（dep_time）：
model3 <- lm(air_time ~ carrier + distance + month + dep_time,
data = flights_train)

predict3_train <- predict(model3, flights_train)
error3_train <- flights_train$air_time - predict3_train
evaluate_ _error(error3_train)
## abs_err std_dev
## 9.312961 12.626790
样本内误差的大小和方差都小幅下降：
predict3_test <- predict(model3, flights_test)
error3_test <- flights_test$air_time - predict3_test
evaluate_ _error(error3_test)
## abs_err std_dev
## 9.38309 12.70168
另外，样本外误差也比 model2 看起来稍好一些。为了比较添加新回归元前后的样本
外误差分布，我们将两条密度曲线相互叠加到一起，如图 7-33 所示。
plot(density(error2_test, na.rm = TRUE),
main = "Empirical distributions of out-of-sample errors")
lines(density(error3_test, na.rm = TRUE), lty = 2)
legend("topright", legend = c("model2", "model3"),
lty = c(1, 2), cex = 0.8,
x.intersp = 0.6, y.intersp = 0.6)

 

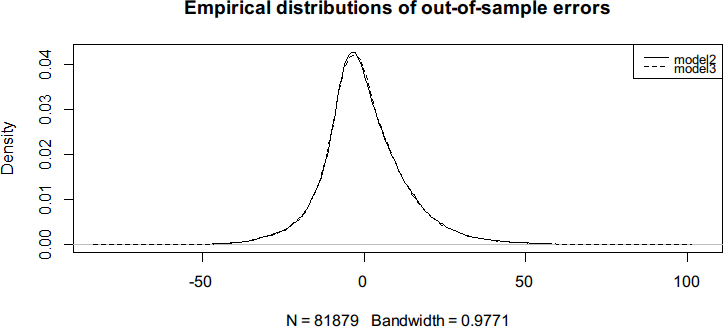
图 7-33
由以上密度图可知，model2 到 model3 模型拟合效果的提升小到可以忽略，即没有
得到明显的改善。