题解 [CF13D] Triangles

传送门

很好的思维/计算几何题，有多种解法

解法1（鬼知道这怎么想到）：
首先是点和三角形关系想到套路「如果一个点位于三角形的内部，那么对于逆时针遍历有向直线，该点总是落在左边」
康康在这里怎么用这个性质
放张图：

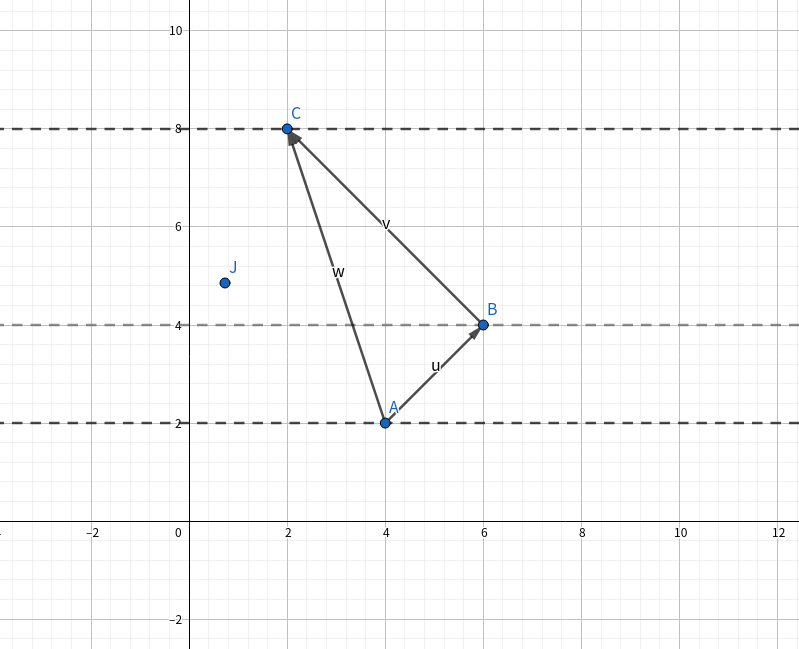
发现如果重定义一条线 $(a, b)$ 的左边为相对于坐标轴的左边，且这个点的纵坐标 $y\in (y_a, y_b]$，则称这个点在这条线左边
如图，点 $J$ 在v的左边但不在u的左边
于是发现图中三角形中没有蓝点的条件是 u左边点数+v左边点数=w左边点数
于是可以预处理 $f_{i, j}$ 代表线段 $(i, j)$ 左边的蓝点数
于是可以check，注意这个做法中枚举的三角形三个点需要满足纵坐标递增

解法2（官方题解）：

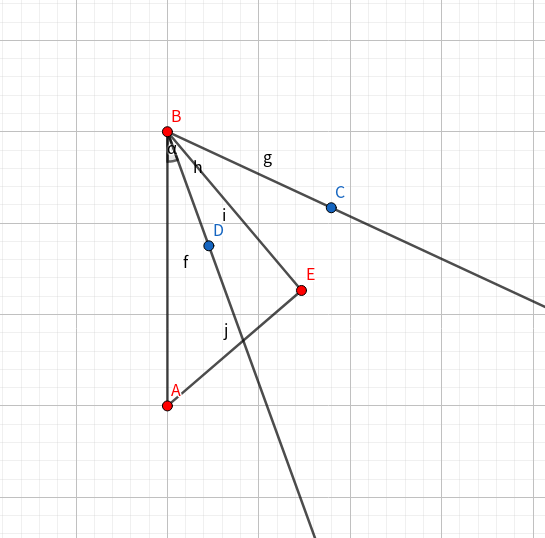
先枚举一条边 $(A, B)$ 将所有其它点按照与点 $A$ 的极角排序
于是按极角从小到大枚举点，记录一个点 $D$ 表示与点B夹角最小的蓝点
然后每当枚举到一个红点时check一下点D在不在形成的三角形中就可以了
正确性很好证，但并不知道如何想

Code:

#include <bits/stdc++.h>
using namespace std;
#define INF 0x3f3f3f3f
#define N 510
#define ll long long
//#define int long long

char buf[1<<21], *p1=buf, *p2=buf;
#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf, 1, 1<<21, stdin)), p1==p2?EOF:*p1++)
inline int read() {
	int ans=0, f=1; char c=getchar();
	while (!isdigit(c)) {if (c=='-') f=-f; c=getchar();}
	while (isdigit(c)) {ans=(ans<<3)+(ans<<1)+(c^48); c=getchar();}
	return ans*f;
}

int n, m;
int f[N][N], ans;
struct point{ll x, y; inline void build() {x=read(); y=read();}}a[N], b[N];
inline bool operator < (point a, point b) {return a.y<b.y;}
struct vec{ll x, y; vec(point a, point b) {x=b.x-a.x; y=b.y-a.y;}};
inline ll operator ^ (vec a, vec b) {return a.x*b.y-b.x*a.y;}
bool toleft(point a, point b, point c) {
	if (c.y>=b.y || c.y<a.y) return 0;
	else return (vec(a, b)^vec(a, c))>0;
}

signed main()
{
	n=read(); m=read();
	for (int i=1; i<=n; ++i) a[i].build();
	for (int i=1; i<=m; ++i) b[i].build();
	sort(a+1, a+n+1);
	for (int i=1; i<=n; ++i)
		for (int j=i+1; j<=n; ++j)
			for (int k=1; k<=m; ++k)
				if (toleft(a[i], a[j], b[k])) ++f[i][j];
	for (int i=1; i<=n; ++i)
		for (int j=i+1; j<=n; ++j)
			for (int k=j+1; k<=n; ++k)
				if (f[i][j]+f[j][k]==f[i][k]) ++ans;
	printf("%d\n", ans);

	return 0;
}