SP174题解

SP174 题解

题面

原题传送门

题意

原题题意等价为如下。

\(0\) 阶图是一个 \(1\times1\) 的黑色格子阵，这个格子是黑色的。

\(i\) 阶图由 \(4\) 个边长为 \(2^{i-1}\) 的 \(i-1\) 阶图以“田”字形拼接成的边长为 \(2^i\) 的图，其中左上角的图是纯白的，其他的图是 \(i-1\) 阶图。

问，给定一个 \(n\) 阶图，将其向右平移 \(X\) 格，向上平移 \(Y\) 格得到的图与原本的图叠放在一起，有多少个格子都是黑色。

思路

首先看到 \(n\) 的范围就知道这题要高精度，这里不多赘述，可以去模板题查看。

接下来，我为格点编号，从左到右，从下到上编号。（因为是往右往上移动，所以这么编号，平移就是加法了，我们就只要考虑进位，如果有减法还得考虑退位。）

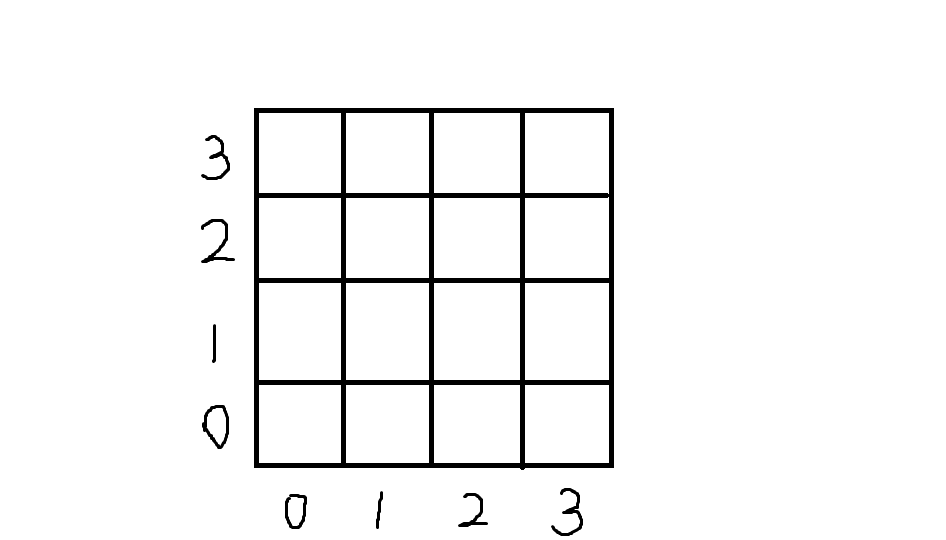
注意到，对于 \(k(k\geqslant1)\) 阶图中的一个格子 \((x,y)\)，它所在的是哪一个 \(k-1\) 阶图只由 \(x,y\) 二进制表示下第 \(k\) 位决定。

1. 若第 \(k\) 位为 \((0,0)\)，则 \((x,y)\) 在左下角。
2. 若第 \(k\) 位为 \((0,1)\)，则 \((x,y)\) 在左上角。
3. 若第 \(k\) 位为 \((1,0)\)，则 \((x,y)\) 在右下角。
4. 若第 \(k\) 位为 \((1,1)\)，则 \((x,y)\) 在右上角。

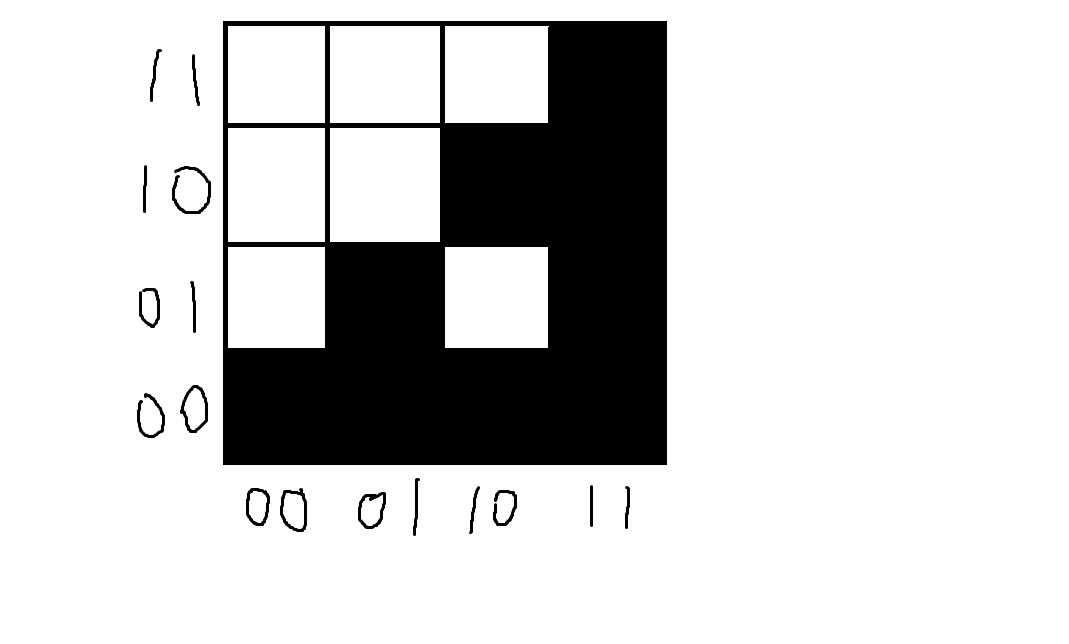
而对于每一个 \(k\) 阶图，左上角都是白色，所以第 \(k\) 位的 \((x,y)\) 为 \((0,0),(1,0),(1,1)\) 时，\((x,y)\) 才有可能是黑色。

所以推广一下，若 \(x,y\) 二进制表示下的任意一位都满足 \(x=1\) 或 \(y=0\) 时，\((x,y)\) 才是黑色。

故我们把问题转化为有多少个 \((x,y)\) 满足 \((x,y)\) 和 \((x+X,y+Y)\) 二进制表示下的任意一位都满足 \(x=1\) 或 \(y=0\)。

这个问题就好解决了，这是经典的数位 dp。

设 \(dp_{i,0/1,0/1}\) 表示 \(i\) 阶图中，上一位的 \(x,y\) 是否进位的黑色的 \((x+X,y+Y)\) 的个数。

转移只要枚举上一位 \((x,y)\) 的情况，判断 \((x,y)\) 是否是黑色，然后再判断 \((x+X,y+Y)\) 是否是黑色即可。

具体请看代码实现。

代码

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
//#define gc getchar
#define gc()(p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
#define ll long long
using namespace std;
const int MN=105;
ll n,x[MN],y[MN];
string s1,s2;
char buf[1<<23],*p1=buf,*p2=buf;
void write(ll n){if(n<0){putchar('-');write(-n);return;}if(n>9)write(n/10);putchar(n%10+'0');}
ll read(){ll x=0,f=1;char ch=gc();while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=gc();}while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=gc();}return x*f;}
class gaojing{
    public:
    ll a[MN];
    gaojing(){memset(a,0,sizeof(a));}
    void clear(){memset(a,0,sizeof(a));}
    void print(){if(a[0]==0)putchar('0');else for(int i=a[0]; i>=1; i--)putchar(a[i]+'0');}
    gaojing(ll x){clear();while(x){a[++a[0]]=x%10;x/=10;}while(a[a[0]]==0&&a[0])a[0]--;}
    // gaojing& opeartor = (ll x){clear();while(x){a[++a[0]]=x%10;x/=10;}while(a[a[0]]==0&&a[0])a[0]--;return *this;}
    gaojing& operator = (string s){clear();for(int i=s.size()-1; i>=0; i--)a[++a[0]]=s[i]-'0';return *this;}
    short cmp(const gaojing& x){if(a[0]>x.a[0])return 1;if(a[0]<x.a[0])return -1;for(int i=a[0]; i>=1; i--){if(a[i]>x.a[i]) return 1;if(a[i]<x.a[i]) return -1;}return 0;}
    bool operator > (const gaojing& x){return cmp(x)==1;}
    bool operator == (const gaojing& x){return cmp(x)==0;}
    bool operator < (const gaojing& x){return cmp(x)==-1;}
    bool operator >= (const gaojing& x){return !(*this<x);}
    bool operator <= (const gaojing& x){return !(*this>x);}
    gaojing operator - (const gaojing& x){gaojing a=*this,c;c.a[0]=a.a[0]>x.a[0]?a.a[0]:x.a[0];for(int i=1; i<=c.a[0]; i++){c.a[i]+=a.a[i]-x.a[i];if(c.a[i]<0){c.a[i]+=10;a.a[i+1]--;}}while(c.a[c.a[0]]==0&&c.a[0])c.a[0]--;return c;}
    gaojing operator + (const gaojing& x){gaojing a=*this,c;c.a[0]=max(a.a[0],x.a[0]);for(int i=1; i<=c.a[0]; i++){c.a[i]+=a.a[i]+x.a[i];if(c.a[i]>9){c.a[i]-=10;a.a[i+1]++;if(i==c.a[0])c.a[0]++;}}while(c.a[c.a[0]]==0&&c.a[0])c.a[0]--;return c;}
    gaojing operator * (const gaojing& x){gaojing c;for(int i=1; i<=a[0]; i++) for(int j=1; j<=x.a[0]; j++) c.a[i+j-1]+=a[i]*x.a[j];c.a[0]=a[0]+x.a[0];for(int i=1; i<=c.a[0]; i++) if(c.a[i]>=10){c.a[i+1]+=c.a[i]/10;c.a[i]%=10;}while(c.a[c.a[0]]==0&&c.a[0]>0)c.a[0]--;return c;}
    gaojing operator / (const ll& x){gaojing c;ll t=0,s=0;bool flag=true;for(int i=a[0]; i>=1; i--){t=s*10+a[i];if(t/x>0||t==0){c.a[++c.a[0]]=t/x;s=t%x;flag=false;}else{s=t;if(!flag)c.a[++c.a[0]]=0;}}reverse(c.a+1,c.a+c.a[0]+1);return c;}
    gaojing operator % (const ll& x){gaojing a=*this,b,c=x;b=a/x;b=b*c;return a-b;}
    gaojing operator ^ (const ll& x){gaojing res=1,a=*this;ll b=x;while(b){if(b&1)res=res*a;a=a*a;b>>=1;}return res;}
}dp[MN][2][2],n1,n2,tmp,zero,one;
void init(){for(int i=1; i<=n; i++) for(int j=0; j<2; j++) for(int k=0; k<2; k++) dp[i][j][k].clear();}
void solve(){
    init();
    cin>>n>>s1>>s2;n1=s1;n2=s2;dp[0][0][0]="1";
    for(int i=0; i<n; i++){tmp=n1%2;x[i]=(tmp==one)?1:0;n1=n1/2;}
    for(int i=0; i<n; i++){tmp=n2%2;y[i]=(tmp==one)?1:0;n2=n2/2;}
    for(int i=0; i<n; i++) for(int a=0; a<2; a++) for(int b=0; b<2; b++) for(int c=0; c<2; c++) for(int d=0; d<2; d++) if((c||!d)&&((a^c^x[i])||!(b^d^y[i]))) dp[i+1][(a+c+x[i])>>1][(b+d+y[i])>>1]=dp[i+1][(a+c+x[i])>>1][(b+d+y[i])>>1]+dp[i][a][b];
    dp[n][0][0].print();putchar('\n');
}
int main(){
    ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
    zero="0";one="1";
    ll T;cin>>T;while(T--)solve();
    return 0;
}//250721

当然，这样来空间会很大，因此我们还可以让 dp 数组滚动起来，这样 \(n\) 的范围就可以来到 \(5000\)，代码如下。

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
//#define gc getchar
#define gc()(p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
#define ll long long
#define ni i&1
#define li i&1^1
using namespace std;
const int MN=5005;
ll n,x[MN],y[MN];
string s1,s2;
char buf[1<<23],*p1=buf,*p2=buf;
void write(ll n){if(n<0){putchar('-');write(-n);return;}if(n>9)write(n/10);putchar(n%10+'0');}
ll read(){ll x=0,f=1;char ch=gc();while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=gc();}while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=gc();}return x*f;}
class gaojing{
    public:
    ll a[MN];
    gaojing(){memset(a,0,sizeof(a));}
    void clear(){memset(a,0,sizeof(a));}
    void print(){if(a[0]==0)putchar('0');else for(int i=a[0]; i>=1; i--)putchar(a[i]+'0');}
    gaojing(ll x){clear();while(x){a[++a[0]]=x%10;x/=10;}while(a[a[0]]==0&&a[0])a[0]--;}
    // gaojing& opeartor = (ll x){clear();while(x){a[++a[0]]=x%10;x/=10;}while(a[a[0]]==0&&a[0])a[0]--;return *this;}
    gaojing& operator = (string s){clear();for(int i=s.size()-1; i>=0; i--)a[++a[0]]=s[i]-'0';return *this;}
    short cmp(const gaojing& x){if(a[0]>x.a[0])return 1;if(a[0]<x.a[0])return -1;for(int i=a[0]; i>=1; i--){if(a[i]>x.a[i]) return 1;if(a[i]<x.a[i]) return -1;}return 0;}
    bool operator > (const gaojing& x){return cmp(x)==1;}
    bool operator == (const gaojing& x){return cmp(x)==0;}
    bool operator < (const gaojing& x){return cmp(x)==-1;}
    bool operator >= (const gaojing& x){return !(*this<x);}
    bool operator <= (const gaojing& x){return !(*this>x);}
    gaojing operator - (const gaojing& x){gaojing a=*this,c;c.a[0]=a.a[0]>x.a[0]?a.a[0]:x.a[0];for(int i=1; i<=c.a[0]; i++){c.a[i]+=a.a[i]-x.a[i];if(c.a[i]<0){c.a[i]+=10;a.a[i+1]--;}}while(c.a[c.a[0]]==0&&c.a[0])c.a[0]--;return c;}
    gaojing operator + (const gaojing& x){gaojing a=*this,c;c.a[0]=max(a.a[0],x.a[0]);for(int i=1; i<=c.a[0]; i++){c.a[i]+=a.a[i]+x.a[i];if(c.a[i]>9){c.a[i]-=10;a.a[i+1]++;if(i==c.a[0])c.a[0]++;}}while(c.a[c.a[0]]==0&&c.a[0])c.a[0]--;return c;}
    gaojing operator * (const gaojing& x){gaojing c;for(int i=1; i<=a[0]; i++) for(int j=1; j<=x.a[0]; j++) c.a[i+j-1]+=a[i]*x.a[j];c.a[0]=a[0]+x.a[0];for(int i=1; i<=c.a[0]; i++) if(c.a[i]>=10){c.a[i+1]+=c.a[i]/10;c.a[i]%=10;}while(c.a[c.a[0]]==0&&c.a[0]>0)c.a[0]--;return c;}
    gaojing operator / (const ll& x){gaojing c;ll t=0,s=0;bool flag=true;for(int i=a[0]; i>=1; i--){t=s*10+a[i];if(t/x>0||t==0){c.a[++c.a[0]]=t/x;s=t%x;flag=false;}else{s=t;if(!flag)c.a[++c.a[0]]=0;}}reverse(c.a+1,c.a+c.a[0]+1);return c;}
    gaojing operator % (const ll& x){gaojing a=*this,b,c=x;b=a/x;b=b*c;return a-b;}
    gaojing operator ^ (const ll& x){gaojing res=1,a=*this;ll b=x;while(b){if(b&1)res=res*a;a=a*a;b>>=1;}return res;}
}dp[2][2][2],n1,n2,tmp,zero,one;
void init(){for(int i=0; i<2; i++) for(int j=0; j<2; j++) for(int k=0; k<2; k++) dp[i][j][k].clear();}
void solve(){
    init();
    cin>>n>>s1>>s2;n1=s1;n2=s2;dp[0][0][0]="1";
    for(int i=0; i<n; i++){tmp=n1%2;x[i]=(tmp==one)?1:0;n1=n1/2;}
    for(int i=0; i<n; i++){tmp=n2%2;y[i]=(tmp==one)?1:0;n2=n2/2;}
    for(int i=0; i<n; i++){
        for(int a=0; a<2; a++) for(int b=0; b<2; b++) dp[li][a][b]=zero;
        for(int a=0; a<2; a++) for(int b=0; b<2; b++) for(int c=0; c<2; c++) for(int d=0; d<2; d++) if((c||!d)&&((a^c^x[i])||!(b^d^y[i]))) dp[li][(a+c+x[i])>>1][(b+d+y[i])>>1]=dp[li][(a+c+x[i])>>1][(b+d+y[i])>>1]+dp[ni][a][b];
    }
    dp[n&1][0][0].print();putchar('\n');
}
int main(){
    ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
    zero="0";one="1";
    ll T;cin>>T;while(T--)solve();
    return 0;
}//250721