2022 China Collegiate Programming Contest (CCPC) Weihai Site ACEGJ
A. Dunai 思维
题意:之前有\(n\)场比赛,有\(n\)个冠军队伍,每个队伍5个人。接下来给你\(m\)个即将参加比赛的人和所在位置(1~5)。问你在保证一个队伍至少有一个冠军在,并且每个位置都要有人。问最多能组成多少个队伍。
思路:我们考虑木桶原理,肯定是最少的那个位置决定最终的。但是又有考虑每个队伍都要有至少一个冠军,那我们贪心的去放,一个冠军放在一个队伍。那么最后的答案就是:\(min(冠军数,最少人数的位置的人数)\)
// AC one more times
// nndbk
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod = 1e9 + 7;
const int N = 2e5 + 10;
int main()
{
ios::sync_with_stdio(false); cin.tie(nullptr), cout.tie(nullptr);
int n,m;
cin>>n;
map<string,bool>mp;
map<int,int>c1,c2;
for(int i = 1;i <= n; i++)
{
for(int j = 1;j <= 5; j++)
{
string x; cin>>x;
mp[x] = true;
}
}
cin>>m;
for(int i = 1;i <= m; i++)
{
string x;
int pos;
cin>>x>>pos;
if(mp.count(x))
c1[pos]++;
c2[pos]++;
}
int mn = 1e9,ans = 0;
for(int i = 1;i <= 5; i++)
mn = min(mn,c2[i]);
for(int i = 1;i <= 5;i++)
ans += c1[i];
cout<<min(ans,mn)<<"\n";
return 0;
}
C. Grass 计算几何
题意:给你\(n\)个点,问你是否能找到5个点,使得在确定这5个点中某一个点为中心点之后其他点到它的连线中不存在别的另外4个中的公共点。

比如上图:\((1)\)符合题意,但是 \((2)\)不符合,因为对于\(AE,AC\)它们除了\(A\)还存在\(E\)这个公共点。
思路:考虑什么情况下是一定不存在的?当且仅当这\(5\)个点都共线。我们可以从斜率的角度考虑。
我们可以考虑随便找\(4\)个点,假设找一开始的\(4\)个点。然后去枚举第\(5\)个点。如果这\(5\)个点不是共线的,那么一定可以满足条件。我们再对于这\(5\)个点去枚举中心点去\(check\)即可。
// AC one more times
// nndbk
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod = 1e9 + 7;
const int N = 2e5 + 10;
int main()
{
ios::sync_with_stdio(false); cin.tie(nullptr), cout.tie(nullptr);
int t;
cin>>t;
while(t--)
{
int n;
cin>>n;
vector<array<int,2>>v;
vector<int>res;
for(int i = 1;i <= n; i++)
{
int x,y; cin>>x>>y;
v.push_back({x,y});
}
auto invalid = [&]()//如果一开始都共线,或者点数小于5那肯定是不行的,否则一定存在
{
int sz = v.size();
if(sz<5)return true;
set<array<int,2>>s;
for(int i = 1; i < sz; i++)
{
int tx = v[i][0]-v[0][0],ty = v[i][1]-v[0][1];
int g = abs(__gcd(tx,ty));
if(tx<0)tx = -tx,ty = -ty;
tx/=g,ty/=g;
s.insert({tx,ty});
}
return s.size() == 1;
};
auto valid_p = [&](int p)//看枚举的第五个点是否合法
{
set<array<int,2>>s;
for(int i = 0; i < 4; i++)
{
int tx = v[i][0]-v[p][0],ty = v[i][1]-v[p][1];
int g = abs(__gcd(tx,ty));
if(tx<0)tx = -tx,ty = -ty;//注意统一负号,不然同侧和异侧会被当成是不同的
tx/=g,ty/=g;
s.insert({tx,ty});
}
return s.size() != 1;
};
if(invalid())
{
cout<<"NO\n";
continue;
}
for(int i = 0;i < 4; i++)
res.push_back(i);
for(int i = 4;i < n; i++)
{
if(valid_p(i))
{
res.push_back(i);
break;
}
}
int cent = 0;
for(int i = 0;i < 5; i++)
{
int cx = v[res[i]][0],cy = v[res[i]][1];
set<array<int,2>>s;
for(int j = 0; j < 5; j++)
{
if(i==j)continue;
int tx = v[res[j]][0]-cx,ty = v[res[j]][1]-cy;
int g = abs(__gcd(tx,ty));
tx/=g,ty/=g;
s.insert({tx,ty});
}
if(s.size()==4)//如果斜率有4种,说明是合法的(因为我们不同方向是不一样的,那么异侧的情况就合法,同侧不合法)
{
cent = res[i];
break;
}
}
cout<<"YES\n";
cout<<v[cent][0]<<" "<<v[cent][1]<<"\n";
for(int i = 0;i < 5; i++)
{
if(res[i]==cent)continue;
cout<<v[res[i]][0]<<" "<<v[res[i]][1]<<"\n";
}
}
return 0;
}
E. Python Will be Faster than C++
题意:给你\(n\)个\(Python\)的版本和运行速度,以及\(C\)++的运行速度。对于未来版本\((>n)\),我们的递推柿子是\(a_i = max(0,2a_{i-1}-a{i-2})\)。
思路:如果前\(n\)个有比\(k\)小的就直接输出,否则就开始递推。注意如果\(a[n]<a[n+1]\)(即递增的),那么只会越来越大。如果前面\(n\)个不满足,后面肯定更不满足的。我们考虑递推\(1e7\)以内的,如果都不行,那么就永远不可能。
// AC one more times
// nndbk
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod = 1e9 + 7;
const int N = 2e7 + 10;
int a[N];
int main()
{
ios::sync_with_stdio(false); cin.tie(nullptr), cout.tie(nullptr);
int n,k;
cin>>n>>k;
for(int i = 1;i <= n; i++)
cin>>a[i];
for(int i = 1;i <= n; i++)
{
if(a[i]<k)
{
cout<<"Python 3."<<i<<" will be faster than C++\n";
return 0;
}
}
int idx = n+1;
while(idx<=1e7&&a[n-1]>a[n])
{
a[idx] = max(0,2*a[idx-1]-a[idx-2]);
if(a[idx]<k)
{
cout<<"Python 3."<<idx<<" will be faster than C++\n";
return 0;
}
idx++;
}
cout<<"Python will never be faster than C++\n";
return 0;
}
G. Grade 2
题意:求\(\sum_{k = l}^{r}[\gcd(kx⊕x,x)=1]\)
思路:打表,发现有循环节。
打表代码:
// AC one more times
// nndbk
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod = 1e9 + 7;
const int N = 2e5 + 10;
int main()
{
ios::sync_with_stdio(false); cin.tie(nullptr), cout.tie(nullptr);
int x; cin>>x;
cout<<"x = "<<x<<"\n";
for(int k = 1;k <= 100; k++)
{
cout<<"k = "<<k<<" res = "<<(__gcd(k*x^x,x)==1)<<"\n";
}
cout<<"\n";
return 0;
}
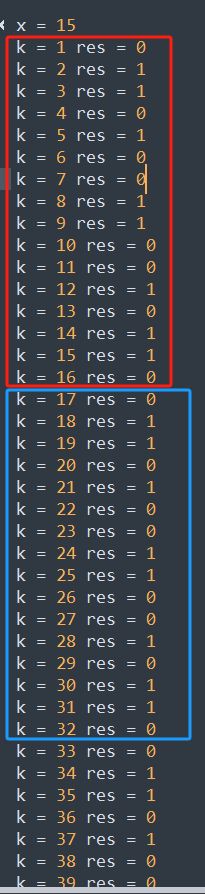
对于\(x = 15\)有(其中0表示满足条件):
对于\(x = 3\)
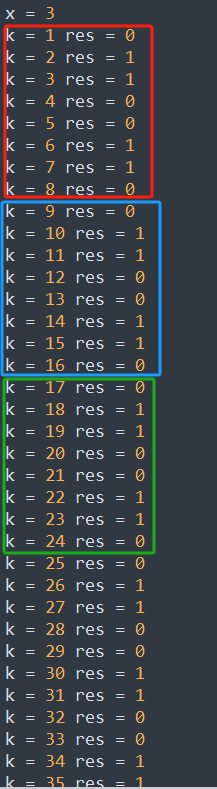
多试几个发现:循环节长度是第一个大于\(x\)的2的幂次。
对于题目\(\sum_{l}^{r}\)我们可以拆成\(\sum_{1}^{r}-\sum_{1}^{l-1}\)
那么长成这样可以考虑用前缀和处理,对于一个循环节里面,我们可以处理出前\(i\)个有多少个\(1\)即\(pre[i]\)
然后我们的答案就是完整的循环节+多出来的部分。
// AC one more times
// nndbk
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod = 1e9 + 7;
const int N = 2e6 + 10;
ll x,n,l,r,pre[N];
int main()
{
ios::sync_with_stdio(false); cin.tie(nullptr), cout.tie(nullptr);
cin>>x>>n;
ll t = x,c= 1;
while(t)
t/=2,c*=2;
for(int i = 1;i <= c; i++)
pre[i] = pre[i-1]+(__gcd(i*x^x,x)==1);
for(int i = 1;i <= n; i++)
{
cin>>l>>r;
l--;
ll res = 0;
res -= (l/c)*pre[c];
res -= pre[l%c];
res += (r/c)*pre[c];
res += pre[r%c];
cout<<res<<"\n";
}
return 0;
}
J. Eat, Sleep, Repeat
题意:给你\(n\)个数字,\(a_1\)到\(a_n\),然后再给你\(k\)个限制,表示\(x_i\)的出现次数不能超过\(y_i\)个。
\(P\)和\(F\)轮流操作,每次选一个数\(-1\)。当且仅当无论选哪个数\(-1\)都不满足限制或者全都是\(0\)的时候输。\(P\)是先手,问最后谁赢?
思路:我们考虑最后最多的操作次数,然后看是奇数还是偶数即可(奇数先手赢)。
我们考虑用\(map\)来记录限制,当限制变成\(0\)了,那么不可能再跨越。我们以\(0\)作为分界,找它的最大可能操作的变化。变完以后记得限制要改变。
// AC one more times
// nndbk
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod = 1e9 + 7;
const int N = 2e5 + 10;
int a[N];
int main()
{
ios::sync_with_stdio(false); cin.tie(nullptr), cout.tie(nullptr);
int t;
cin>>t;
while(t--)
{
int n,k;
cin>>n>>k;
for(int i = 1;i <= n; i++)
cin>>a[i];
sort(a+1,a+1+n);
map<ll,int>mp;
set<ll>s;
for(int i = 1;i <= k; i++)
{
int x,y;
cin>>x>>y;
mp[x] = y;
if(y==0)s.insert(x);
}
s.insert(-1),s.insert(1e18);//手动加入上下界
for(int i = 1;i <= n; i++)
{
if(mp.count(a[i])==0)
mp[a[i]] = n;
}
if(mp.count(0)==0)
mp[0] = n;
// cout<<"mp:\n";
// for(auto [x,c]:mp)
// cout<<x<<" "<<c<<"\n";
int cnt = 0;
for(int i = 1;i <= n; i++)
{
int x = a[i];
auto p = lower_bound(s.begin(),s.end(),x);
p = prev(p);
// cout<<"p:";
// cout<<*p<<"\n";
if(*p==-1){
cnt += x,mp[0]--;
if(mp[0]==0)s.insert(0);
}else{
cnt += x-(*p+1);
if(mp.count(*p+1)){
mp[*p+1]--;
if(mp[*p+1]==0)s.insert(*p+1);
}
}
}
//cout<<"cnt = "<<cnt<<"\n";
if(cnt%2)cout<<"Pico\n";
else cout<<"FuuFuu\n";
}
return 0;
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号