Cartesian tree(笛卡尔树)
1.概念
比如拿最小的当根建树,中序遍历是原数组
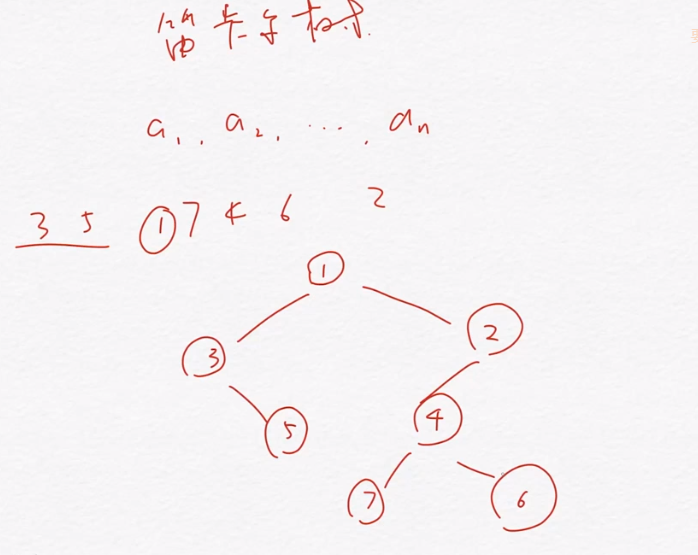
笛卡尔树是形如上图的一棵树,满足:
①:堆的性质,以上图为例(小根堆),两个儿子的值大于等于他们的父亲
②:二叉搜索树性质:左边子树的下标比根小,右边子树的下标比根大。显然中序遍历可得原数组
③:询问下标为\(i\)到下标为\(j(i<j)\)之间的最小值,就是找\((i,j)\)的LCA
2.性质
- 区间最小值(RMQ),LCA的值,比如上图4和6的LCA是2,表示我们4,6,2这个区间里面的最小值是2
- 找y左边第一个<=y的数就是y往上看第一个向左拐的数
3.构造(增量法)
对每个前缀考虑
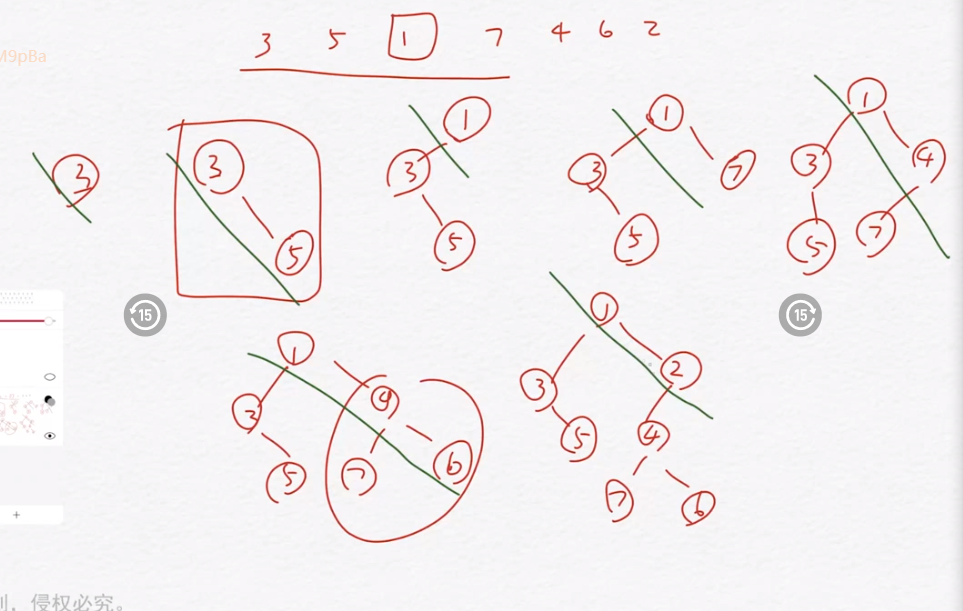
我们发现只有右链是会变的,一旦走到左边,那就不会变了
比如举个例子:该链插入4
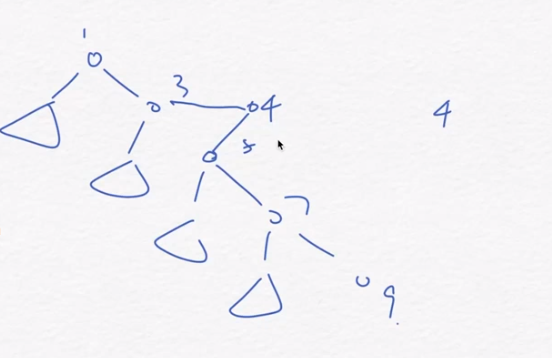
就会变成:
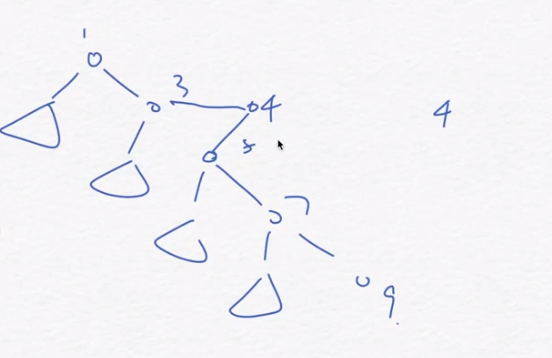
因此我们考虑用一个单调栈维护右链:
具体过程就是:
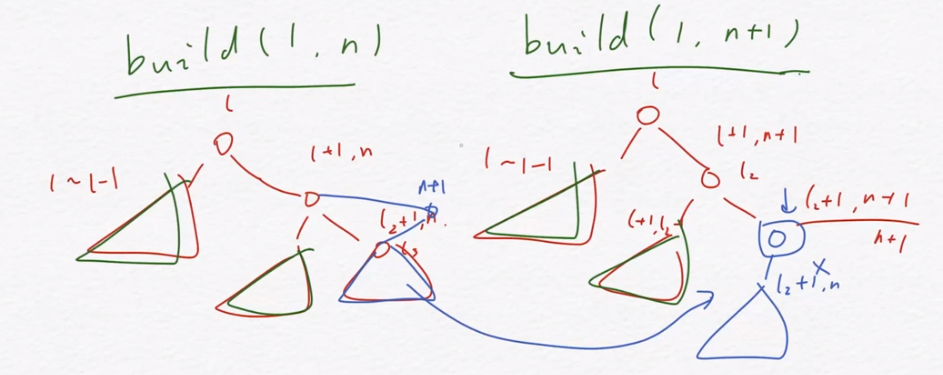
我们倒着for,如果这个数比我们新插入的数大的话,我们就pop,否则就把新加入的数插入变成右儿子(保证右链的单调性),原来pop掉的变为左儿子。
每个元素至多进栈一次,出栈一次,O(n)完成构造
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 201000;
int n,a[N],l[N],r[N];
void build()
{
stack<int>st;
int root = 0;
for(int i = 1;i<=n;i++)
{
int last = 0;//在栈里面最后一个被弹出的节点
while(!st.empty()&&a[st.top()]>a[i])
{
last = st.top();
st.pop();
}
if(!st.empty())r[st.top()] = i;//新加入的元素设为栈顶元素的右儿子
else root = i;
l[i] = last;
st.push(i);
}
// for(int i = 1;i<=n;i++)
// cout<<"i = "<<i<<" a[i] = "<<a[i]<<" l[i] = "<<l[i]<<" r[i] = "<<r[i]<<endl;
}
int main()
{
cin>>n;
for(int i = 1;i<=n;i++)
cin>>a[i];
build();
}
/*
7
3 5 1 7 4 6 2
*/
4.用处
能用一个树形的结构去揭示一个序列区间最小值问题,实现把序列问题转化为树上问题
比如:求所有区间的最小值之和
\(\sum_{i = 1}^{n}\sum_{j = i+1}^{n}min(Ai...Aj)\)
做法一:找到左边第一个小于它的元素\(L_i\),右边第一个小于它的元素\(R_i\),那么它的贡献区间是\([L_{i+1},R_{i-1}]\),那么贡献值就是\(A_i\times (i-L_i+1)\times (R_i - i+1)\)
做法二:从笛卡尔树的角度看,还是考虑每个数的贡献,即这个数在多少个区间里是最小值,实际上就是看看它的左儿子有多大它的右儿子有多大。相当于多少对点LCA等于这个点本身,也就是左端点选择左子树的点或者这个点本身,右端点选择右子树或者这个点本身。即:\(A_i\times (L_{size}+1)\times (R_{size}+1)\)
实现了把序列问题转化为树上问题。
eg1笛卡尔树
给你一个\(1∼n\)的排列\(p_1,p_2,…,p_n\)。
让你找到一个\(1∼n\)的排列\(q\),满足对于任意区间\([l,r](1≤l≤r≤n)\),满足\(p_l,p_{l+1},…,p_r\)中的最小值的位置,和\(q_l,q_{l+1},…,q_r\)的最小值的位置相同。
输出满足条件的字典序最小的\(q\)。
思路:从笛卡尔树的角度来看,两个序列的最小值位置相同,说明两个序列的笛卡尔树一样。因为要求字典序最小的,我们按照先序遍历把数字填上去。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 2010000;
int n,a[N],l[N],r[N],ans[N],cnt;
void dfs(int x)
{
ans[x] = ++cnt;
if(l[x])dfs(l[x]);
if(r[x])dfs(r[x]);
}
void build()
{
stack<int>st;
int root = 0;
for(int i = 1;i<=n;i++)
{
int last = 0;//在栈里面最后一个被弹出的节点
while(!st.empty()&&a[st.top()]>a[i])
{
last = st.top();
st.pop();
}
if(!st.empty())r[st.top()] = i;//新加入的元素设为栈顶元素的右儿子
else root = i;
l[i] = last;
st.push(i);
}
// for(int i = 1;i<=n;i++)
// cout<<"i = "<<i<<" a[i] = "<<a[i]<<" l[i] = "<<l[i]<<" r[i] = "<<r[i]<<endl;
dfs(root);
}
int main()
{
cin>>n;
for(int i = 1;i<=n;i++)
cin>>a[i];
build();
for(int i = 1;i<=n;i++)
cout<<ans[i]<<" ";
cout<<endl;
}
/*
7
3 5 1 7 4 6 2
*/
ST table
1.思想
一般用于解决RMQ (Range Minimum/Maximum Query)问题。
倍增的思想1—>2—>4—>8—>16
我们先处理出所有区间长度为1的最小值
\(f[i][j]\)表示左端点为\(i\),区间长度为\(2^j\)的区间的最小值。即:\([i,i+2^j-1] (i+2^j-1 \le n)\)
\(f[i][0] = a[i]\)
\(f[i][1] = min(a[i],a[i+1])\)
\(f[i][2] = min(f[i][1],f[i+2][1])\)

那么:\(f[i][j] = min(f[i][j-1],f[i+2^{j-1}][j-1])\)
对于一段区间\([l,r]\),\(len = r-l+1\)
我们要找\(2^x \le len\)的最大的\(x\)(因为最大的\(x\)一定能使得我们找的这两个区间把整个区间覆盖。)
这样我们一定能找到两个长度为\(2^x\)的区间,分别是\([l,l+2^x-1]\)和\([r-2^x+1,r]\)(这两个区间有交集是没有关系的)
2.局限性
- 易看出,只有当区间中重叠的部分对最终答案无影响时,才能使用 st 表。
比如区间&,|,gcd是可以的,但像求区间*或者区间+就是不行的了
- 不能进行修改操作
3. 复杂度:\(O(n \log n)\)建表,\(O(1)\)查询
4. eg.RMQ
给\(n\)个数\(a1,a2,…,an\),\(q\)个询问。
每个询问给定两个数\(l,r\),求出\(al,al+1,…,ar\)中的最大值。
//读入
unsigned int A, B, C;
inline unsigned int rng61() {
A ^= A << 16;
A ^= A >> 5;
A ^= A << 1;
unsigned int t = A;
A = B;
B = C;
C ^= t ^ A;
return C;
}
int main(){
scanf("%d%d%u%u%u", &n, &q, &A, &B, &C);
for (int i = 1; i <= n; i++) {
a[i] = rng61();
}
for (int i = 1; i <= q; i++) {
unsigned int l = rng61() % n + 1, r = rng61() % n + 1;
if (l > r) swap(l, r);
}
}
代码:
//O(nlogn)建表,O(1)查询
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1010000;
int n,q,lg[N];
unsigned int A,B,C,a[N],ans;
//unsigned int f[N][22];
unsigned int f[22][N];//尽量让靠里的那一维连续的变,让内存访问更加连续
inline unsigned int rng61() {
A ^= A << 16;
A ^= A >> 5;
A ^= A << 1;
unsigned int t = A;
A = B;
B = C;
C ^= t ^ A;
return C;
}
int main(){
scanf("%d%d%u%u%u", &n, &q, &A, &B, &C);
for (int i = 1; i <= n; i++) {
a[i] = rng61();
f[0][i] = a[i];
}
// for(int j = 1;j<=20;j++)
// for(int i = 1;i+(1<<j)-1<=n;i++)
// f[i][j] = max(f[i][j-1],f[i+(1<<(j-1))][j-1]);
for(int j = 1;j<=20;j++)
for(int i = 1;i+(1<<j)-1<=n;i++)
f[j][i] = max(f[j-1][i],f[j-1][i+(1<<(j-1))]);
lg[1] = 0;//2^0
for(int i = 2;i<=n;i++)//手写,对2求lg取下整
lg[i] = lg[i/2]+1;
for (int i = 1; i <= q; i++) {
unsigned int l = rng61() % n + 1, r = rng61() % n + 1;
if (l > r) swap(l, r);
//写法1
//int len = lg[r-l+1];
//写法2
//int len = __lg(r-l+1);
//写法3
int len = 31-__builtin_clz(r-l+1);//__builtin_clz数二进制位的前导0
//2^x<=len,2^(x+1)>len
ans ^= max(f[len][l],f[len][r-(1<<len)+1]);
}
cout<<ans<<endl;
}

5.ST 表维护其他信息
除了RQM之外,还有其它的「可重复贡献问题」,例如「区间按位和」、「区间按位或」、「区间 GCD」,ST 表都能高效地解决。
6.板子代码
const int N = 5e4+10;
struct S_T {
// op 函数需要支持两个可以重叠的区间进行合并
// 例如 min、 max、 gcd、 lcm 等
int f[22][N], lg[N];
void build(int n) {
lg[0] = -1;
for (int i = 1; i <= n; ++i) {
f[0][i] = a[i];
lg[i] = lg[i / 2] + 1;
}
for (int i = 1; i <= 20; ++i)
for (int j = 1; j + (1 << i) - 1 <= n; ++j)
f[i][j] = max(f[i - 1][j], f[i - 1][j + (1 << (i - 1))]);
}
int query(int l, int r) {
int len = lg[r - l + 1];
return max(f[len][l], f[len][r - (1 << len) + 1]);
}
} ST;
Weighted Disjoint-set(带权并查集)
eg带权并查集
给你\(n\)个变量\(a_1,a_2,…,a_n\),一开始不知道这些数是多少。
你要执行\(q\)次操作。
1 l r x,给你一条线索,表示\(a_l−a_r=x\),如果与已知条件矛盾,那么忽略这次操作。2 l r回答\(a_l−a_r\),如果现在的线索无法推出答案,那么忽略这次操作。
强制在线(读一个操作一个):
有一个变量\(t\),一开始\(t=0\),每次未被忽略的查询操作之后,\(t\)会变成答案的绝对值,也就是\(|a_l−a_r|\)。每次操作输入的是加密后的\(l^′,r^′,\)实际上的\(l=(l^′+t)\bmod n+1,r=(r^′+t)\bmod n+1\)。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 201000;
int n,q,fa[N];
ll w[N];
int find(int x)
{
if(x==fa[x])return x;
int p = fa[x];
find(p);//先把fa[x]做一个路径压缩,假设现在的fa[p] = q
/*
w[x] = a[x]-a[p]
fa[p] = q , w[p]:a[p]-a[q]
fa[x] = p , w[x]:a[x]-a[p]
a[x] - a[p] + a[p] - a[q] = a[x]+a[p]
*/
w[x] = w[x]+w[p];
return fa[x] = fa[p];
}
int main()
{
cin>>n>>q;
//w[i] = a[i]-a[fa[i]];
for(int i = 1;i<=n;i++)fa[i] = i,w[i] = 0;
ll t = 0;
for(int i = 0;i<q;i++)
{
int op,l,r;
cin>>op>>l>>r;
l = (l+t)%n + 1;
r = (r+t)%n + 1;
if(op==2)
{
if(find(l)!=find(r))continue;
else cout<<w[l]-w[r]<<endl;
t = abs(w[l]-w[r]);
}
else if(op==1)
{
int x;
cin>>x;
if(find(l)==find(r))continue;
/*
w[fa[l]] = a[fa[l]]-a[fa[r]];
a[l]-a[r] = x;
w[l] = a[l]-a[fa[l]],w[r] = a[r]-a[fa[r]];
a[l] - w[l] = a[fa[l]],a[r]-w[r] = a[fa[r]]
w[fa[l]] = a[l]-w[l]-(a[r]-w[r])
*/
//先改权值再变父亲
w[fa[l]] = x-w[l]+w[r];
fa[fa[l]] = fa[r];
}
}
return 0;
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号