【洛谷P1983】车站分级 [NOIP2013普及]

今天做了两道绿题 调的有点久

还是拓扑排序的 这题主要是建图的关系 至于拓扑排序倒没过于深入

P1983 [NOIP 2013 普及组] 车站分级

题目背景

NOIP2013 普及组 T4

题目描述

一条单向的铁路线上，依次有编号为 \(1, 2, …, n\) 的 $n $ 个火车站。每个火车站都有一个级别，最低为 \(1\) 级。现有若干趟车次在这条线路上行驶，每一趟都满足如下要求：如果这趟车次停靠了火车站 \(x\)，则始发站、终点站之间所有级别大于等于火车站 \(x\) 的都必须停靠。
注意：起始站和终点站自然也算作事先已知需要停靠的站点。

例如，下表是 $ 5 $ 趟车次的运行情况。其中，前 $ 4$ 趟车次均满足要求，而第 \(5\) 趟车次由于停靠了 \(3\) 号火车站（\(2\) 级）却未停靠途经的 \(6\) 号火车站（亦为 \(2\) 级）而不满足要求。

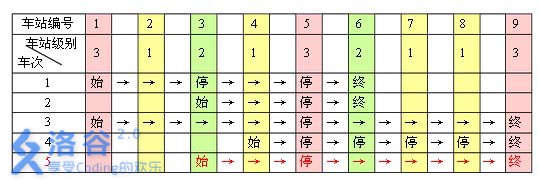
现有 \(m\) 趟车次的运行情况（全部满足要求），试推算这 $ n$ 个火车站至少分为几个不同的级别。

输入格式

第一行包含 \(2\) 个正整数 \(n, m\)，用一个空格隔开。

第 \(i + 1\) 行 \((1 ≤ i ≤ m)\) 中，首先是一个正整数 \(s_i\ (2 ≤ s_i ≤ n)\)，表示第 $ i$ 趟车次有 \(s_i\) 个停靠站；接下来有 $ s_i$ 个正整数，表示所有停靠站的编号，从小到大排列。每两个数之间用一个空格隔开。输入保证所有的车次都满足要求。

输出格式

一个正整数，即 \(n\) 个火车站最少划分的级别数。

输入输出样例 #1

输入 #1

9 2 
4 1 3 5 6 
3 3 5 6

输出 #1

2

输入输出样例 #2

输入 #2

9 3 
4 1 3 5 6 
3 3 5 6 
3 1 5 9

输出 #2

3

说明/提示

对于 $ 20%$ 的数据，\(1 ≤ n, m ≤ 10\)；

对于 \(50\%\) 的数据，\(1 ≤ n, m ≤ 100\)；

对于 \(100\%\) 的数据，\(1 ≤ n, m ≤ 1000\)。

解法&&个人感想

我们来看看题干所说的 “对于一个停靠的站，等级大于等于它的站一定停靠”
我们不能判断其他停靠站跟它是同级还是大于 但是我们反着想想
WOW!只要不停地就是比它小的 于是思路就出来了
注意：vis数组是必要的 因为给出的是该死的第i个车站 而且第1个是起始站 第n个是终止站
所以不能用st[i]去循环 而应该在一开始打个标记
欧耶！
这题我采用了邻接矩阵和vector来存图
vector是动态数组 也就是根据输入自动调整大小的数组
a.push_back(x)表示把元素x插入vector的末尾
而a.size()返回a的元素数量 注意 vector的下标从0开始

#include<bits/stdc++.h>
#define ll long long
using namespace std;
int n,m,tot,s;
int edge[1005][1005],deg[1005];
vector<int>pvz[1005];
int vis[1005];
int st[1005];
struct node{
    int ver,rank;
};
queue<node>q;
int ans;
int main(){
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;i++){
        memset(st,0,sizeof(st));
        memset(vis,0,sizeof(vis));
        scanf("%d",&s);
        for(int j=1;j<=s;j++){
            scanf("%d",&st[j]);
            vis[st[j]]=1;
        }
        for(int j=1;j<=s;j++){
            for(int k=st[1];k<=st[s];k++){
                if(!vis[k]&&!edge[k][st[j]]){
                    edge[k][st[j]]=1;
                    pvz[k].push_back(st[j]);
                    deg[st[j]]++;
                }
            }
        }
    }
    for(int i=1;i<=n;i++){
        if(!deg[i]){
            q.push(node{i,1});
        }
    }
    while(!q.empty()){
        node x=q.front();q.pop();
        for(int i=0;i<pvz[x.ver].size();i++){
            int y=pvz[x.ver][i];
            --deg[y];
            if(!deg[y]){
                ans=max(ans,x.rank+1);
                q.push(node{y,x.rank+1});
            }
        }
    }
    printf("%d",ans);
    system("pause");
    return 0;
}