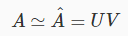

目标函数
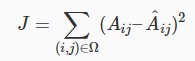
优化目标函数
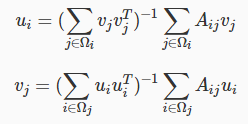
利用坐标下降法,依次更新u和v的值。u和v的先后顺序无所谓,只要保证两者是交替更新的就好。这种方法又称为alternating least squares(ALS)。
增加偏置项
在行和列都增加一个常数项,去除每个用户的个体影响。
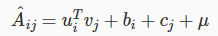
更新的公式修正为
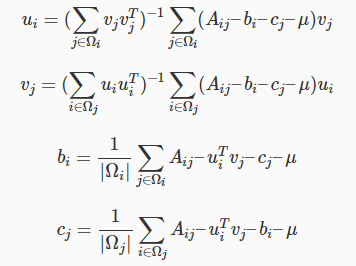
增加正则项
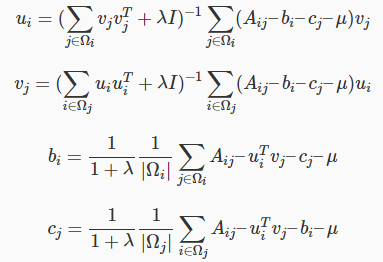
实现代码
## 初始化矩阵
U = np.random.randn(M, K) / K
V = np.random.randn(K, N) / K
B = np.zeros(M)
C = np.zeros(N)
## 迭代T步,每一步依次更新B、U、C、V矩阵
for t in xrange(T):
# update B
for i in xrange(M):
if i in ratings_by_i:
accum = 0
for j, r in ratings_by_i[i]:
accum += (r - U[i,:].dot(V[:,j]) - C[j] - mu)
B[i] = accum / (1 + reg) / len(ratings_by_i[i])
# update U
for i in xrange(M):
if i in ratings_by_i:
matrix = np.zeros((K, K)) + reg*np.eye(K)
vector = np.zeros(K)
for j, r in ratings_by_i[i]:
matrix += np.outer(V[:,j], V[:,j])
vector += (r - B[i] - C[j] - mu)*V[:,j]
U[i,:] = np.linalg.solve(matrix, vector)
# update C
for j in xrange(N):
if j in ratings_by_j:
accum = 0
for i, r in ratings_by_j[j]:
accum += (r - U[i,:].dot(V[:,j]) - B[i] - mu)
C[j] = accum / (1 + reg) / len(ratings_by_j[j])
# update V
for j in xrange(N):
if j in ratings_by_j:
matrix = np.zeros((K, K)) + reg*np.eye(K)
vector = np.zeros(K)
for i, r in ratings_by_j[j]:
matrix += np.outer(U[i,:], U[i,:])
vector += (r - B[i] - C[j] - mu)*U[i,:]
V[:,j] = np.linalg.solve(matrix, vector)




 浙公网安备 33010602011771号
浙公网安备 33010602011771号