Trie

835. Trie字符串统计

模板题：

维护一个字符串集合，支持两种操作：

1. I x 向集合中插入一个字符串 x；
2. Q x 询问一个字符串在集合中出现了多少次。

共有 N 个操作，所有输入的字符串总长度不超过 10^5，字符串仅包含小写英文字母。

输入格式

第一行包含整数 N，表示操作数。

接下来 N 行，每行包含一个操作指令，指令为 I x 或 Q x 中的一种。

输出格式

对于每个询问指令 Q x，都要输出一个整数作为结果，表示 x 在集合中出现的次数。

每个结果占一行。

数据范围

1≤N≤2∗10^4

输入样例：

5
I abc
Q abc
Q ab
I ab
Q ab

输出样例：

1
0
1

个人理解：

个人感觉这个Trie是比较简单理解的，直接给上注意点还有图解；

AC代码：

#include <iostream>
using namespace std;
//定义：不超过 10^5；
//符合要求即可；
const int Ma=100010;
//这里的26是a~z(字符串仅包含小写英文字母)
//con[Ma]是记录Trie每个父节点最后一个的子节点(有图解)；
//idx是记录c的“下标”；
int Trie[Ma][26],con[Ma],idx;   //这里容易误解的点：26 a~z并不是层级；而是以a~z带头的父节点；
char str[Ma];
//这是构造Trie树；
void insert(char str[]){
    int p=0;
    for(int i=0;str[i];i++){
        int c=str[i]-'a';
        //如果没有记录这个字符，idx开辟一个位置来兜住；
        if(!Trie[p][c]){
            Trie[p][c]=++idx;
        }
        //p来指向下一个；
        p=Trie[p][c];
    }
    //记录最后一个字符的位置的个数； 比如 abcd 记录一次，abcd 再来一次 con[p]=2;
    con[p]++;
}
//查找
int search(char str[]){
    int p=0;
    for(int i=0;str[i];i++){
        int c=str[i]-'a';
        //按顺序找下去，不对直接返回0；
        if(!Trie[p][c]){
            return 0;
        }else{
            //指向下一个；
            p=Trie[p][c];
        }
    }
    //返回结果；
    return con[p];
}
int main(){
    int n;
    cin >> n;
    while(n--){
        char c;
        cin >> c >> str;
        if(c=='I'){
           insert(str);
        }else{
            cout << search(str) << endl;
        }
    }
    return 0;
}

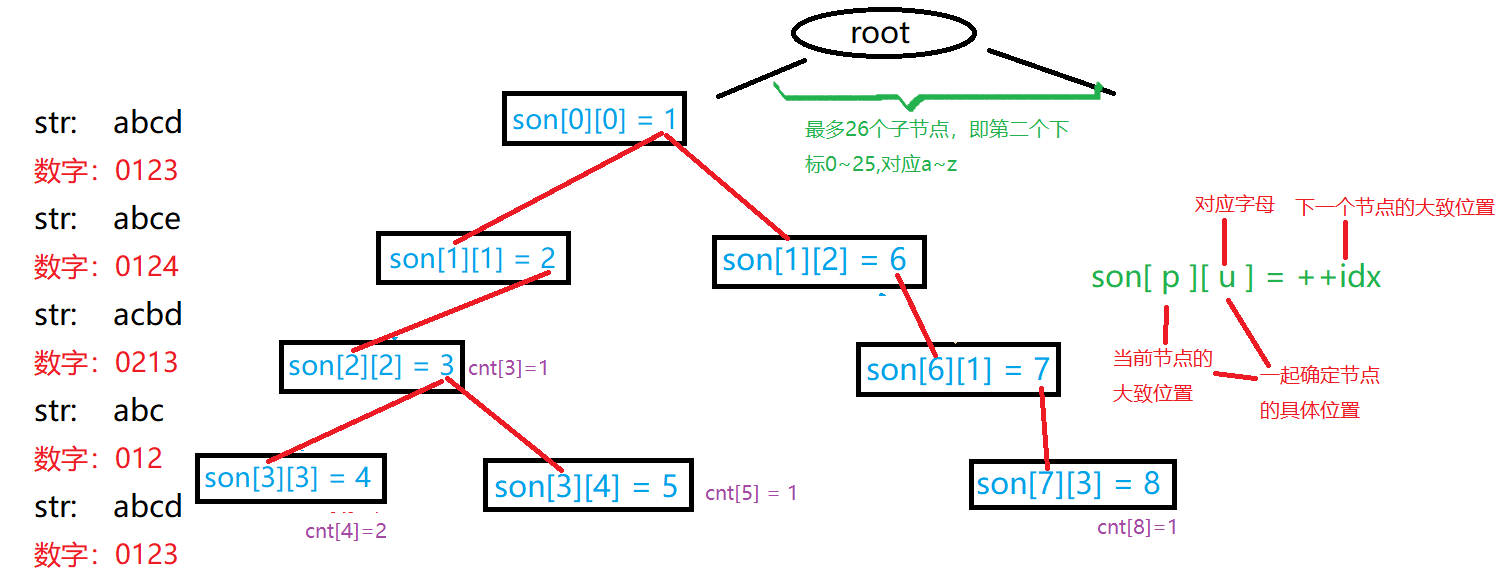
图解：来源--------AC 四谷夕雨

解疑：

Trie[p][c]=++idx; //这是什么？idx干什么用的？    

• 一维下标：父节点的位置（层级）
  二维下标：当前节点的位置(a_z->025)
  值：当前节点的id(用idx标识，唯一性)
• 这里是可以自己图画手推的：手推也可能就会发现用这种方法的话，是会浪费一层里的空间的.......这就自定义想了，在下面我会给出一些例题，是很明显的吧，有优化可以q我
• 自己手推很重要，本人在没手推之前，总是觉得字符之间会重复什么的.......,手推才意识到idx的强大，idx是即将待操作的结点下标 (看自己的理解吧)；
• 哦对，在这以前要知道怎么构建Trie，要不然够呛，比如abcd 的“路径”是可以保存 abc的只需记录最后一个节点；

相关例题：

AC. 最大异或对：

在给定的 N 个整数 A1，A2……AN中选出两个进行 xor（异或）运算，得到的结果最大是多少？

输入格式

第一行输入一个整数 N。

第二行输入 N 个整数 A1～AN。

输出格式

输出一个整数表示答案。

数据范围

1≤N≤10^5
0≤Ai<2^31

输入样例：

3
1 2 3

输出样例：

3

解析：

• 异或对：随便两个数进行逻辑异或操作求出两两匹配之间最大的异或值；

• 逻辑异或操作： 异或（XOR）

  逻辑异或运算，运算规则：相异为一，相同为零。即两个操作数不一样时结果为1，两个操作数相同时结果为0。（这都是二进制的形式比较）

  操作数1	操作数2	结果值
  1	1	0
  1	0	1
  0	1	1
  0	0	0

AC代码（暴力）：

#include<iostream>
using namespace std;
int sum[100005],a[100005];
int main(){
    int n,ans=0;
    cin >> n;
    for(int i=1;i<=n;i++){
        cin >> a[i];
        //前缀和；
        sum[i]=sum[i-1]^a[i];
    }
    //两两比较；
    for(int i=1;i<=n;i++){
        for(int j=1;j<=i;j++){
            ans=max(ans,sum[i]^sum[j-1]);
        }
    }
    cout << ans << endl;
    return 0;
}

• 暴力的做法是:第一个循环时间复杂度O(n),第二个O(N^2)，时间复杂度肯定是爆掉的；在下面用Trie优化一下

AC代码（Trie）：

#include <iostream>
using namespace std;
//0≤Ai<2^31所以最高位是第30位。
//因为是正数，所以要保证第一位是1
const int Ma=3100010,N=1e5+10;
#define int long long
int e[Ma][2],idx;
int a[N];
//构建Trie；
void insert(int x){
    int p=0;
    for(int i=30;i>=0;i--){
        int u=x >> i & 1;
        if(!e[p][u]) e[p][u]=++idx;
        p=e[p][u];
    }
}
int search(int x){
    int p=0,res=0;
    for(int i=30;i>=0;i--){
        //捋明白位移情况在配合上述的Trie手推就很好理解了
        int u=x >> i & 1;
        //判断同层有没有相反的数，只有1或者0，1取反找0，0取反找1；没有走原路；(建议画图理解)
        if(e[p][!u]){
            p=e[p][!u];
            res=res*2+1;  //这里跟转10进制一样的0*10+n
        }
        else{
            //走原路，不要把取反的值带过来看了......
            p=e[p][u];
            res=res*2+0;
        }
    }
    return res;
}
signed main(){
    int n;
    cin >> n;
    if(n==1){int x;cin >> x;cout << x << endl;return 0;}
    for(int i=0;i<n;i++){
        cin >> a[i];
        insert(a[i]);
    }
    int res=0;
    for(int i=0;i<n;i++){
        res=max(res,search(a[i]));
    }
    cout << res << '\n';
}

总结：手推, 手推 , 还是手推；

再分享一道马蹄的题:

MT2055最大异或和:

给定一串手链，每个珠子被赋予一个价值wi,现要从中截取连续的一段，使得他们的异或和最大（注意，手链还未串上）。

格式

输入格式：

第11行包含一个正整数N；
第22行n个正整数wi​，表示珠子价格。

输出格式：

一个正整数，输出最大异或和。

样例 1

输入：

5
1 2 3 4 5

输出：

7

备注

其中：n≤2000,wi≤100000

早期代码: 前缀和+暴力

#include<iostream>
using namespace std;
int sum[100005],a[100005];
int main(){
    int n,ans=0;
    cin >> n;
    for(int i=1;i<=n;i++){
        cin >> a[i];
        //前缀和;
        sum[i]=sum[i-1]^a[i];
    }
    //第一个和每一个进行比较;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=i;j++){
            ans=max(ans,sum[i]^sum[j-1]);
        }
    }
    cout << ans << endl;
    return 0;
}

后期的优化: 前缀和+Trie

#include <iostream>
using namespace std;
const int Ma=3100010,N=1e5+10;
#define int long long
int e[Ma][2],idx;
int a[N];
void insert(int x){
    int p=0;
    for(int i=30;i>=0;i--){
        int u=x >> i & 1;
        if(!e[p][u]) e[p][u]=++idx;
        p=e[p][u];
    }
}
int search(int x){
    int p=0,res=0;
    for(int i=30;i>=0;i--){
        int u=x >> i & 1;
        if(e[p][!u]){
            p=e[p][!u];
            res=res*2+1;
        }
        else{
            p=e[p][u];
            res=res*2+0;
        }
    }
    return res;
}
signed main(){
    int n;
    cin >> n;
    if(n==1){int x;cin >> x;cout << x << endl;return 0;}
    for(int i=0;i<n;i++){
        cin >> a[i];
        //前缀和
        a[i]^=a[i-1];
        insert(a[i]);
    }
    int res=0;
    for(int i=0;i<n;i++){
        res=max(res,search(a[i]));
    }
    cout << res << '\n';
}

• 这题是跟上述不同的:这个是实现前缀和的异或相加,在进行异或对操作;