数据结构模板
数据结构
离散化
结构体实现
#include <bits/stdc++.h>
using namespace std;
const int maxn = 100;
//input:
//5
//9 1 0 5 4
int n = 0;
struct node
{
int x, id;
}a[maxn];
int b[maxn] = {};
bool cmp(node &nd1, node &nd2)
{
return nd1.x < nd2.x;
}
int main()
{
scanf("%d", &n);
for(int i=1; i<=n; i++)
{
scanf("%d", &a[i].x);
a[i].id = i;
}
sort(a+1, a+1+n, cmp);
for(int i=1; i<=n; i++) b[a[i].id] = i;
for(int i=1; i<=n; i++) printf("%d ", b[i]);
}
使用STL实现-方法一
#include <bits/stdc++.h>
using namespace std;
const int maxn = 100;
//input:
//6
//9 1 1 0 5 4
int n = 0;
int a[maxn] = {}, b[maxn] = {};
int main()
{
scanf("%d", &n);
for(int i=1; i<=n; i++)
{
scanf("%d", &a[i]);
b[i] = a[i];
}
sort(a+1, a+1+n);
int cnt = unique(a+1, a+1+n) - (a+1);
for(int i=1; i<=n; i++)
{
b[i] = lower_bound(a+1, a+1+cnt, b[i]) - a;
}
for(int i=1; i<=n; i++) printf("%d ", b[i]);
}
使用STL实现-方法二
#include <bits/stdc++.h>
using namespace std;
const int maxn = 100;
//input:
//5
//9 1 0 5 4
int n = 0;
map<int, int> mp;
int cnt = 0;
int a[maxn] = {}, b[maxn] = {};
int main()
{
scanf("%d", &n);
for(int i=1; i<=n; i++)
{
scanf("%d", &a[i]);
b[i] = a[i];
}
sort(a+1, a+1+n);
for(int i=1; i<=n; i++) mp[a[i]] = ++cnt;
for(int i=1; i<=n; i++) printf("%d ", mp[b[i]]);
}
并查集
朴素并查集
例题:提高题库 161.亲戚
#include <bits/stdc++.h>
using namespace std;
const int inf = 0x3f3f3f3f;
const int maxn = 20010;
int n = 0, m = 0, q = 0;
int fa[maxn] = {};
//查找祖先节点
int getfa(int x)
{
if(x == fa[x]) return fa[x];
return fa[x] = getfa(fa[x]);
}
//将y合并到x
void merge(int x, int y)
{
int fx = getfa(x);
int fy = getfa(y);
if(fx != fy) fa[fy] = fx;
}
int main()
{
int x = 0, y = 0;
scanf("%d%d", &n, &m);
//初始化
for(int i=1; i<=n; i++) fa[i] = i;
for(int i=1; i<=m; i++)
{
scanf("%d%d", &x, &y);
merge(x, y);
}
scanf("%d", &q);
for(int i=1; i<=q; i++)
{
scanf("%d%d", &x, &y);
int fx = getfa(x);
int fy = getfa(y);
if(fx == fy) printf("Yes\n");
else printf("No\n");
}
return 0;
}
维护size的并查集
例题:提高题库 163.打击犯罪
const int maxn = 1010;
int n = 0;
//fa[]存储每个点的祖宗节点, size[]只有祖宗节点的有意义,表示祖宗节点所在集合中的点的数量
int fa[maxn] = {}, size[maxn] = {};
//返回x的祖宗节点
int findset(int x)
{
if(fa[x] != x) fa[x] = findset(fa[x]);
return fa[x];
}
//合并a和b所在的两个集合:
void merge(int x, int y)
{
int fx = findset(x), fy = findset(y);
if(fx != fy)
{
fa[fy] = fx;
size[fx] += size[fy];
}
}
//初始化,假定节点编号是1~n
for(int i=1; i<=n; i++)
{
fa[i] = i;
size[i] = 1;
}
维护到祖宗节点距离的并查集
例题:提高题库 167.信息传递
const int maxn = 200010;
int n = 0;
//fa[]存储每个点的祖宗节点, d[]存储x到fa[x]的距离
int fa[maxn] = {}, d[maxn] = {};
//返回x的祖宗节点
int findset(int x)
{
if(fa[x] != x)
{
int y = findset(fa[x]);
d[x] += d[fa[x]];
fa[x] = y;
}
return fa[x];
}
//将y所在集合合并到x集合
void merge(int x, int y)
{
int fx = findset(x), fy = findset(y);
if(fx != fy)
{
fa[fy] = fx;
d[fy] = d[x] + 1;
}
}
// 初始化,假定节点编号是1~n
for(int i=1; i<=n; i++) fa[i] = i;
树状数组
单点修改,区间查询
例题:提高题库 232.数列操作
#include <bits/stdc++.h>
using namespace std;
const int maxn = 100010;
int n = 0, m = 0;
int c[maxn] = {};
int lowbit(int x)
{
return x & -x;
}
void add(int x, int val)
{
while(x <= n)
{
c[x] += val;
x += lowbit(x);
}
}
int getsum(int x)
{
int res = 0;
while(x)
{
res += c[x];
x -= lowbit(x);
}
return res;
}
int main()
{
char op[5];
int a = 0, b = 0;
scanf("%d", &n);
for(int i=1; i<=n; i++)
{
scanf("%d", &a);
add(i, a);
}
scanf("%d", &m);
for(int i=1; i<=m; i++)
{
scanf("%s%d%d", op, &a, &b);
if(op[0] == 'S') //区间查询
{
printf("%d\n", getsum(b) - getsum(a-1));
}
else //单点修改
{
add(a, b);
}
}
return 0;
}
区间修改,单点查询
例题:提高题库 210 数列操作b
#include <bits/stdc++.h>
using namespace std;
const int maxn = 100010;
int n = 0, m = 0;
int a[maxn] = {}, c[maxn] = {};
int lowbit(int x)
{
return x & -x;
}
void add(int x, int val)
{
while(x <= n)
{
c[x] += val;
x += lowbit(x);
}
}
int getsum(int x)
{
int res = 0;
while(x)
{
res += c[x];
x -= lowbit(x);
}
return res;
}
int main()
{
char op[5];
int x = 0, y = 0, z = 0;
scanf("%d", &n);
for(int i=1; i<=n; i++)
{
scanf("%d", &a[i]);
}
scanf("%d", &m);
for(int i=1; i<=m; i++)
{
scanf("%s", op);
if(op[0] == 'Q') //单点查询
{
scanf("%d", &x);
printf("%d\n", getsum(x) + a[x]);
}
else //区间修改
{
scanf("%d%d%d", &x, &y, &z);
add(x, z);
add(y+1, -z);
}
}
return 0;
}
区间修改,区间查询
例题:提高题库 235 数列操作c
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 100010;
int n = 0, m = 0;
int a[maxn] = {};
ll c1[maxn] = {}, c2[maxn] = {};
int lowbit(int x)
{
return x & -x;
}
void add(int x, int val)
{
ll val2 = 1ll * val * x;
while(x <= n)
{
c1[x] += val;
c2[x] += val2;
x += lowbit(x);
}
}
ll getsum1(int x)
{
ll res = 0;
while(x)
{
res += c1[x];
x -= lowbit(x);
}
return res;
}
ll getsum2(int x)
{
ll res = 0;
while(x)
{
res += c2[x];
x -= lowbit(x);
}
return res;
}
ll getsum(int l, int r)
{
ll res1 = getsum1(r) * (r + 1) - getsum1(l-1) * l;
ll res2 = getsum2(r) - getsum2(l-1);
return res1 - res2;
}
int main()
{
char op[5];
int x = 0, y = 0, z = 0;
scanf("%d", &n);
for(int i=1; i<=n; i++) scanf("%d", &a[i]);
for(int i=n; i>=2; i--) a[i] = a[i] - a[i-1];
for(int i=1; i<=n; i++) add(i, a[i]);
scanf("%d", &m);
for(int i=1; i<=m; i++)
{
scanf("%s", op);
if(op[0] == 'A') //区间修改
{
scanf("%d%d%d", &x, &y, &z);
add(x, z);
add(y+1, -z);
}
else //区间查询
{
scanf("%d%d", &x, &y);
printf("%lld\n", getsum(x, y));
}
}
return 0;
}
求逆序对
树状数组开到值域的大小,将原数组按数值倒序存到树状数组中,
每存一个数值,给对应位置+1,这样当存的值为\(x\)时,
\(sum(x-1)\)即\(x-1\)的前缀和即为\(x\)对应的逆序对的个数
注意:如果值域较大,需要离散化
例题:求逆序对个数
https://h.hszxoj.com/d/gyktg/p/HZTG109?tid=66b3378e4a2d69bf4ecdd081
#include <bits/stdc++.h>
using namespace std;
/*
树状数组求逆序对
树状数组开到值域的大小,将原数组按数值倒序存到树状数组中,
每存一个数值,给对应位置+1,这样当存的值为x时,
sum(x-1)即x-1的前缀和即为x对应的逆序对的个数
注意:如果值域较大,需要离散化
*/
typedef long long ll;
const int maxn = 3000010;
int n = 0;
//a表示原序列,b表示离散化后的序列,c为树状数组
int a[maxn] = {}, b[maxn] = {}, c[maxn] = {};
int lowbit(int x)
{
return x & (-x);
}
void add(int x, int val)
{
while(x <= n)
{
c[x] += val;
x += lowbit(x);
}
}
ll getsum(int x)
{
ll res = 0;
while(x)
{
res += c[x];
x -= lowbit(x);
}
return res;
}
int main()
{
scanf("%d", &n);
for(int i=1; i<=n; i++)
{
scanf("%d", &a[i]);
b[i] = a[i];
}
sort(a+1, a+1+n);
int cnt = unique(a+1, a+1+n) - (a+1);
for(int i=1; i<=n; i++)
{
b[i] = lower_bound(a+1, a+1+cnt, b[i]) - a;
}
ll ans = 0;
for(int i=n; i>=1; i--)
{
ans += getsum(b[i] - 1);
add(b[i], 1);
}
printf("%lld", ans);
}
二维树状数组
单点修改,区间查询
例题:提高题库 201.移动电话
#include <bits/stdc++.h>
using namespace std;
//二维树状数组板子题
const int maxn = 1050;
int n = 0;
int a[maxn][maxn] = {}, c[maxn][maxn] = {};
int lowbit(int x)
{
return x & (-x);
}
//单点加
//修改(x, y)这个点的值
void add(int x, int y, int val)
{
for(int i=x; i<=n; i+=lowbit(i))
{
for(int j=y; j<=n; j+=lowbit(j))
{
c[i][j] += val;
}
}
}
//求(0, 0)到(x, y)之间矩阵的和
int getsum(int x, int y)
{
int res = 0;
for(int i=x; i>0; i-=lowbit(i))
{
for(int j=y; j>0; j-=lowbit(j))
{
res += c[i][j];
}
}
return res;
}
//求子矩阵和,子矩阵x满足l<=x<=r,子矩阵y满足b<=y<=t
int sum(int l, int b, int r, int t)
{
int res = 0;
res = getsum(r, t) - getsum(l-1, t) - getsum(r, b-1) + getsum(l-1, b-1);
return res;
}
int main()
{
int op = 0;
int x = 0, y = 0, val = 0;
int l = 0, b = 0, r = 0, t = 0;
scanf("%d%d", &op, &n);
while(1)
{
scanf("%d", &op);
if(op == 3) break;
else if(op == 1)
{
scanf("%d%d%d", &x, &y, &val);
add(x+1, y+1, val);
}
else if(op == 2)
{
scanf("%d%d%d%d", &l, &b, &r, &t);
int res = sum(l+1, b+1, r+1, t+1);
printf("%d\n", res);
}
}
return 0;
}
线段树
线段树基础
1、线段树是竞赛中常用来维护区间信息的数据结构
2、主要操作:
单点修改,区间查询
区间修改,单点查询
区间修改,区间查询
3、原理:
线段树是一颗完全二叉树,用来维护一段区间的信息,每个节点管某一段的信息
线段树中若某个节点为\(p\),则他的左儿子为\(2p\),右儿子为\(2p+1\)
4、线段树的节点个数一般开4倍的区间长度,oi-wiki上有证明
5、线段树常见操作:
建线段树(build)
更新操作(update)
查询操作(query)
向上回溯(pushup)
向下延迟更新(pushdown)
单点修改,区间查询
例题:提高题库 232.数列操作
#include <bits/stdc++.h>
using namespace std;
//预编译命令,做符号代换
#define lson (rt << 1)
#define rson (rt << 1 | 1)
const int maxn = 1e5 + 10;
int n = 0, m = 0;
struct node
{
int l, r, sum;
}tree[maxn << 2];
int a[maxn] = {};
void pushup(int rt)
{
tree[rt].sum = tree[lson].sum + tree[rson].sum;
}
//建树
void Build(int rt, int l, int r)
{
tree[rt].l = l;
tree[rt].r = r; //节点信息初始化
if(l == r) //到叶节点
{
tree[rt].sum = a[l];
return;
}
int mid = (l + r) >> 1;
Build(lson, l, mid);
Build(rson, mid+1, r);
//子树建好后,回溯时更新父节点信息
pushup(rt);
}
void Update(int rt, int pos, int val)
{
if(tree[rt].l == tree[rt].r) //找到对应的叶子节点
{
tree[rt].sum += val;
return;
}
int mid = (tree[rt].l + tree[rt].r) >> 1;
if(pos <= mid) Update(lson, pos, val);
else Update(rson, pos, val);
pushup(rt);
}
//当前节点为rt,要查询的区间是[l, r]
int Query(int rt, int l, int r)
{
//如果节点表示的区间是查询区间的真子集
if(l<=tree[rt].l && tree[rt].r<=r)
{
return tree[rt].sum;
}
int mid = (tree[rt].l + tree[rt].r) >> 1;
if(r <= mid) return Query(lson, l, r);
else if(l > mid) return Query(rson, l, r);
else return Query(lson, l, r) + Query(rson, l, r);
}
int main()
{
char op[5];
int x = 0, y = 0;
scanf("%d", &n);
if(n == 0) return 0;
for(int i=1; i<=n; i++) scanf("%d", &a[i]);
Build(1, 1, n);
scanf("%d", &m);
for(int i=1; i<=m; i++)
{
scanf("%s%d%d", op, &x, &y);
if(op[0] == 'S')
{
printf("%d\n", Query(1, x, y));
}
else
{
Update(1, x, y);
}
}
return 0;
}
区间修改,单点查询
例题:提高题库 210 数列操作b
#include <bits/stdc++.h>
using namespace std;
//预编译命令,做符号代换
#define lson (rt << 1)
#define rson (rt << 1 | 1)
const int maxn = 1e5 + 10;
int n = 0, m = 0;
struct node
{
int l, r, sum;
int lazy; //延迟标记
}tree[maxn << 2];
int a[maxn] = {};
void pushup(int rt)
{
tree[rt].sum = tree[lson].sum + tree[rson].sum;
}
//把当前节点rt的延迟标记下放到左右儿子
void pushdown(int rt)
{
if(tree[rt].lazy) //此节点有延迟标记
{
int lz = tree[rt].lazy;
tree[rt].lazy = 0; //记住要清零
tree[lson].lazy += lz;
tree[rson].lazy += lz;
tree[lson].sum += lz * (tree[lson].r - tree[lson].l + 1);
tree[rson].sum += lz * (tree[rson].r - tree[rson].l + 1);
}
}
//建树
void Build(int rt, int l, int r)
{
tree[rt].l = l;
tree[rt].r = r; //节点信息初始化
if(l == r) //到叶节点
{
tree[rt].sum = a[l];
return;
}
int mid = (l + r) >> 1;
Build(lson, l, mid);
Build(rson, mid+1, r);
//子树建好后,回溯时更新父节点信息
pushup(rt);
}
void Update(int rt, int l, int r, int val)
{
//更新区间完全覆盖节点表示的区间
if(l<=tree[rt].l && tree[rt].r<=r)
{
tree[rt].lazy += val;
tree[rt].sum += val * (tree[rt].r - tree[rt].l + 1);
return;
}
//如果不能完全覆盖,此时需要向下递归,要下放标记
pushdown(rt);
int mid = (tree[rt].l + tree[rt].r) >> 1;
if(l <= mid) Update(lson, l, r, val);
if(r > mid) Update(rson, l, r, val);
pushup(rt);
}
//当前节点为rt,要查询的点是pos
int Query(int rt, int pos)
{
//左右边界相等,说明找到了该pos点
if(tree[rt].l == tree[rt].r)
{
return tree[rt].sum;
}
//如果不能完全覆盖,此时需要向下递归,要下放标记
pushdown(rt);
int mid = (tree[rt].l + tree[rt].r) >> 1;
if(pos <= mid) return Query(lson, pos);
if(pos > mid) return Query(rson, pos);
return 0;
}
int main()
{
char op[10];
int x = 0, y = 0, z = 0;
scanf("%d", &n);
if(n == 0) return 0;
for(int i=1; i<=n; i++) scanf("%d", &a[i]);
Build(1, 1, n);
scanf("%d", &m);
for(int i=1; i<=m; i++)
{
scanf("%s", op);
if(op[0] == 'Q')
{
scanf("%d", &x);
printf("%d\n", Query(1, x));
}
else
{
scanf("%d%d%d", &x, &y, &z);
Update(1, x, y, z);
}
}
return 0;
}
区间修改,区间查询
例题:提高题库 235 数列操作c
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
//预编译命令,做符号代换
#define lson (rt << 1)
#define rson (rt << 1 | 1)
const int maxn = 1e5 + 10;
int n = 0, m = 0;
struct node
{
int l, r;
ll sum;
int lazy; //延迟标记
}tree[maxn << 2];
int a[maxn] = {};
void pushup(int rt)
{
tree[rt].sum = tree[lson].sum + tree[rson].sum;
}
//把当前节点rt的延迟标记下放到左右儿子
void pushdown(int rt)
{
if(tree[rt].lazy) //此节点有延迟标记
{
int lz = tree[rt].lazy;
tree[rt].lazy = 0; //记住要清零
tree[lson].lazy += lz;
tree[rson].lazy += lz;
tree[lson].sum += lz * (tree[lson].r - tree[lson].l + 1);
tree[rson].sum += lz * (tree[rson].r - tree[rson].l + 1);
}
}
//建树
void Build(int rt, int l, int r)
{
tree[rt].l = l;
tree[rt].r = r; //节点信息初始化
if(l == r) //到叶节点
{
tree[rt].sum = a[l];
return;
}
int mid = (l + r) >> 1;
Build(lson, l, mid);
Build(rson, mid+1, r);
//子树建好后,回溯时更新父节点信息
pushup(rt);
}
void Update(int rt, int l, int r, int val)
{
//更新区间完全覆盖节点表示的区间
if(l<=tree[rt].l && tree[rt].r<=r)
{
tree[rt].lazy += val;
tree[rt].sum += val * (tree[rt].r - tree[rt].l + 1);
return;
}
//如果不能完全覆盖,此时需要向下递归,要下放标记
pushdown(rt);
int mid = (tree[rt].l + tree[rt].r) >> 1;
if(l <= mid) Update(lson, l, r, val);
if(r > mid) Update(rson, l, r, val);
pushup(rt);
}
//当前节点为rt,要查询的区间是[l, r]
long long Query(int rt, int l, int r)
{
//如果节点表示的区间是查询区间的真子集
if(l<=tree[rt].l && tree[rt].r<=r)
{
return tree[rt].sum;
}
//如果不能完全覆盖,此时需要向下递归,要下放标记
pushdown(rt);
int mid = (tree[rt].l + tree[rt].r) >> 1;
if(r <= mid) return Query(lson, l, r);
else if(l > mid) return Query(rson, l, r);
else return Query(lson, l, r) + Query(rson, l, r);
}
int main()
{
char op[10];
int x = 0, y = 0, z = 0;
scanf("%d", &n);
if(n == 0) return 0;
for(int i=1; i<=n; i++) scanf("%d", &a[i]);
Build(1, 1, n);
scanf("%d", &m);
for(int i=1; i<=m; i++)
{
scanf("%s", op);
if(op[0] == 'S')
{
scanf("%d%d", &x, &y);
printf("%lld\n", Query(1, x, y));
}
else
{
scanf("%d%d%d", &x, &y, &z);
Update(1, x, y, z);
}
}
return 0;
}
动态开点&权值线段树
1、动态开点核心思想: 结点只有在有需要的时候才被创建
2、动态开点原理:
上面讲到,普通线段树需要开\(4n\)大小的数组,为节省空间,我们可以不一次性建好树,而是在更新操作(update)时,再建立结点。
这时不再用\(2p\)和\(2p+1\)代表\(p\)的左右儿子,而是用\(ls\)和\(rs\)记录儿子的编号
3、动态开点空间计算:
单次操作的时间复杂度是不变的,为\(O(logn)\)。由于每次操作都有可能创建并访问全新的一系列节点,因此m次单点操作后节点的数量规模是\(O(mlogn)\),节点的数组开到\(mlogn\)即可
4、权值线段树的理解:
权值线段树就是用线段树维护一个桶,他可以以\(O(logv)\) (\(v\)为值域)查询某个范围内数出现的总次数。
它常常可以代替平衡树使用
5、权值线段树需要按值域开空间,当值域过大时需要离散化或动态开点
6、权值线段树举例:
我们现有一个长度为10的数组{1,5,2,3,4,1,3,4,4,4}
1 出现了 2 次,2 出现了 1 次,3 出现了 2 次,4 出现了 4 次,5 出现了 1 次。
则这个线段树长这样:
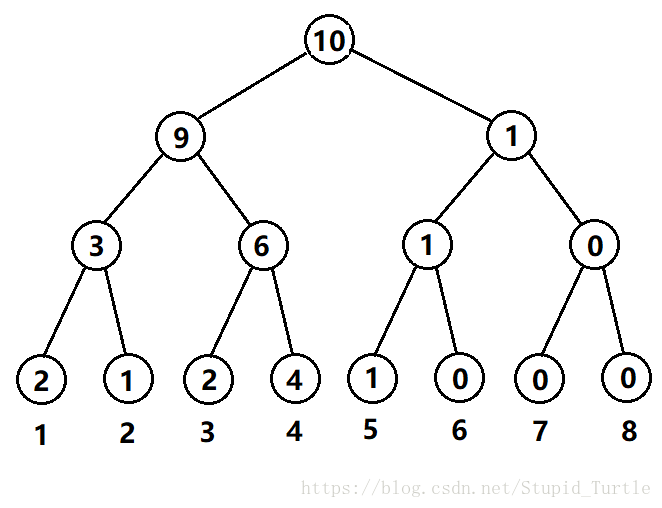
每个叶子节点的值:代表这个值出现的次数
非叶子节点的值:代表了某一个值域内,所有值出现次数的和
上图中并非所有的点都需要,可以动态开点来实现
6、权值线段树的用途:
求某个数\(x\)的排名
求排名为\(x\)的数值
求某个数的前趋
求某个数的后继
求数列中低\(k大/小\)的数
7、例题: 普通平衡树
题库:h.hszxoj.com
#include <bits/stdc++.h>
using namespace std;
/*
动态开点权值线段树
*/
#define lson tree[rt].ls
#define rson tree[rt].rs
const int maxn = 1e5 + 10;
int n = 0;
//建立一棵权值线段树
//底层叶子节点的数量即为数字的值域[-1e7,1e7]
//树的高度为log(2e7)≈25
//所以线段树点数理论为maxn*25,保险起见开30*maxn
struct node
{
int ls, rs, cnt, num;
}tree[maxn*30];
int root = 0, segtot = 0;
//动态开点
//给pos这个值的数量增加val个,若val为负数,则为减少val个
void update(int &rt, int l, int r, int pos, int val)
{
if(!rt) rt = ++segtot;
if(l == r)
{
tree[rt].num = pos;
tree[rt].cnt += val;
return;
}
int mid = (l + r) >> 1;
if(pos <= mid) update(lson, l, mid, pos, val);
else update(rson, mid+1, r, pos, val);
tree[rt].cnt = tree[lson].cnt + tree[rson].cnt;
}
//查询区间[L,R]数字的个数
//这里的区间[L,R]指的是值域,所谓该函数会把值域[L,R]之间所有数返回,包括重复的数字
int query(int rt, int l, int r, int L, int R)
{
if(!rt) return 0;
if(L <= l && r <= R) return tree[rt].cnt;
int ans = 0;
int mid = (l + r) / 2;
if(L <= mid) ans += query(lson, l, mid, L, R);
if(mid < R) ans += query(rson, mid + 1, r, L, R);
return ans;
}
//查询第k小的元素(排名为k的数)
//这里是指从小到大第k个数,重复数字的排名不一样,会按顺序往下排
int queryk(int rt, int l, int r, int k)
{
if(!rt) return -0x3f3f3f3f;
if(l == r) return tree[rt].num;
int mid = (l + r) >> 1;
//因为是从小到大排,所以比较左子树,小于左子树的数量,就在左子树中找
if(k <= tree[lson].cnt)
{
return queryk(lson, l, mid, k);
}
else
{
return queryk(rson, mid+1, r, k - tree[lson].cnt);
}
}
int main()
{
int opt = 0, x = 0, y = 0;
scanf("%d", &n);
while(n--)
{
scanf("%d%d", &opt, &x);
if(opt == 1) //插入一个x数
{
update(root, 1, 2e7+1, x, 1);
}
else if(opt == 2) //删除一个x数
{
update(root, 1, 2e7+1, x, -1);
}
else if(opt == 3) //查询x数的排名
{
//先找到所有[-1e7,x-1]之间的数的数量
//那么x的排名就是该数量+1
y = query(root, 1, 2e7+1, -1e7, x - 1);
printf("%d\n", y + 1);
}
else if(opt == 4) //查询排名为x的数
{
y = queryk(root, 1, 2e7+1, x);
printf("%d\n", y);
}
else if(opt == 5) //求x的前趋
{
//x的前趋指小于x的数中最大的那个
//先求出[-1e7,x-1]之间的数的数量y
//那么排名为y的数就是x的前趋
y = query(root, 1, 2e7+1, -1e7, x - 1);
y = queryk(root, 1, 2e7+1, y);
printf("%d\n", y);
}
else if(opt == 6) //求x的后继
{
//x的后继指大于x的数中最小的那个
//先求出[-1e7,x]之间的数的数量y
//那么排名为y+1的数就是x的后继
int t = 0;
y = query(root, 1, 2e7+1, -1e7, x);
t = queryk(root, 1, 2e7+1, y + 1);
printf("%d\n", t);
}
}
return 0;
}
线段树合并
1、概念: 线段树合并是指建立一棵新的线段树,这棵线段树的每个节点都是两颗原线段树对应节点合并后的结果。
2、线段树合并常被用于维护树上或是图上的信息
3、我们不可能真的每次建满一棵新的线段树,因此需要使用动态开点线段树
ps:线段树合并不会产生新的节点,做题时计算节点数量时要注意
4、合并过程:
线段树合并的过程本质上相当暴力
假设两颗线段树为A和B,我们从1号节点开始递归合并
递归到某个节点时,如果A树或B树上的对应节点为空,直接返回另一个树上对应节点,这里运用了动态开点线段树的特性
如果递归到叶子节点,我们合并两棵树上的对应节点
最后,根据子节点更新当前节点并返回。
5、时间复杂度:
对于两颗满的线段树,合并操作的复杂度是\(O(nlogn)\)的。
实际情况下,使用的常常是权值线段树,总点数和\(n\)的规模相差并不大。
并且合并时一般不会重复地合并某个线段树,所以最终增加的点数大致是\(O(nlogn)\)级别的。
这样,总的复杂度就是\(O(nlogn)\)级别的。
例题:2009.Promotion Counting
h.hszxoj.com
#include <bits/stdc++.h>
using namespace std;
#define lson tree[rt].ls
#define rson tree[rt].rs
const int maxn = 1e5 + 10;
int n = 0, len = 0; //n为原始长度,len为离散化后的长度
int a[maxn] = {}, b[maxn] = {};
//邻接链表存图
int h[maxn] = {}, to[maxn] = {}, nxt[maxn] = {}, tot = 0;
//线段树变量
int root[maxn] = {}, segtot = 0;
//为树的每个节点建立一棵权值线段树,每个权值线段树只标记一个值
//离散化后,值的范围为maxn,所以每插入一个值,需要开log(maxn)≈17个点
//线段树合并不会产生新节点,所以tree开20*maxn个节点就够了
struct node
{
int ls, rs, cnt;
}tree[20*maxn];
//存储答案
int ans[maxn] = {};
void addedge(int x, int y)
{
to[++tot] = y;
nxt[tot] = h[x];
h[x] = tot;
}
//权值线段树加点
void update(int &rt, int l, int r, int pos, int val)
{
if(!rt) rt = ++segtot;
if(l == r)
{
tree[rt].cnt += val;
return;
}
int mid = (l + r) >> 1;
if(pos <= mid) update(lson, l, mid, pos, val);
else update(rson, mid+1, r, pos, val);
tree[rt].cnt = tree[lson].cnt + tree[rson].cnt;
}
//线段树合并
int segmerge(int ra, int rb)
{
if(!ra) return rb;
if(!rb) return ra;
tree[ra].cnt += tree[rb].cnt;
tree[ra].ls = segmerge(tree[ra].ls, tree[rb].ls);
tree[ra].rs = segmerge(tree[ra].rs, tree[rb].rs);
return ra;
}
//查询以rt为根节点的权值线段树中值>=val的个数
int query(int rt, int l, int r, int val)
{
if(!rt) return 0;
if(l == r) return tree[rt].cnt;
int mid = (l + r) >> 1;
if(val <= mid) return query(lson, l, mid, val) + tree[rson].cnt;
return query(rson, mid+1, r, val);
}
//遍历整棵树,并不断将子树合并到父节点
void dfs(int x)
{
for(int i=h[x]; i; i=nxt[i])
{
int y = to[i];
dfs(y);
root[x] = segmerge(root[x], root[y]);
}
ans[x] = query(root[x], 1, len, a[x]) - 1;
}
int main()
{
int x = 0;
scanf("%d", &n);
for(int i=1; i<=n; i++)
{
scanf("%d", &a[i]);
b[i] = a[i];
}
//离散化
sort(b+1, b+1+n);
len = unique(b+1, b+1+n) - (b+1);
for(int i=1; i<=n; i++)
{
a[i] = lower_bound(b+1, b+1+n, a[i]) - b;
update(root[i], 1, len, a[i], 1);
}
//读边
for(int i=2; i<=n; i++)
{
scanf("%d", &x);
addedge(x, i);
}
dfs(1);
for(int i=1; i<=n; i++) printf("%d\n", ans[i]);
return 0;
}
单调队列
例题
例题:249.窗口
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e6+10;
int n = 0, k = 0;
int a[maxn] = {};
deque<int> q; //双端队列
int main()
{
scanf("%d%d", &n, &k);
for(int i=1; i<=n; i++) scanf("%d", &a[i]);
//求最小值,单调递减队列
for(int i=1; i<=n; i++)
{
if(i>k && q.front()==i-k) q.pop_front(); //越界元素出队
while(q.size() && a[q.back()]>a[i]) q.pop_back(); //将队尾不合法元素出队
q.push_back(i);
if(i >= k) printf("%d ", a[q.front()]);
}
printf("\n");
while(q.size()) q.pop_front(); //清空队列
//求最大值,单调递增队列
for(int i=1; i<=n; i++)
{
if(i>k && q.front()==i-k) q.pop_front(); //越界元素出队
while(q.size() && a[q.back()]<a[i]) q.pop_back(); //将队尾不合法元素出队
q.push_back(i);
if(i >= k) printf("%d ", a[q.front()]);
}
return 0;
}
ST算法
例题
例题:346.均衡队形
#include <bits/stdc++.h>
using namespace std;
const int maxn = 50010;
int n = 0, q = 0;
int a[maxn] = {}, f[maxn][30] = {}, g[maxn][30] = {};
//ST算法求最大值
int getmax(int l, int r)
{
int k = log2(r - l + 1);
return max(f[l][k], f[r-(1<<k)+1][k]);
}
//ST算法求最小值
int getmin(int l, int r)
{
int k = log2(r - l + 1);
return min(g[l][k], g[r-(1<<k)+1][k]);
}
int main()
{
scanf("%d%d", &n, &q);
for(int i=1; i<=n; i++)
{
scanf("%d", &a[i]);
f[i][0] = g[i][0] = a[i];
}
//ST算法初始化
int t = log2(n) + 1;
for(int j=1; j<t; j++)
{
for(int i=1; i+(1<<j)-1<=n; i++)
{
f[i][j] = max(f[i][j-1], f[i+(1<<(j-1))][j-1]);
g[i][j] = min(g[i][j-1], g[i+(1<<(j-1))][j-1]);
}
}
int x = 0, y = 0;
for(int i=1; i<=q; i++)
{
scanf("%d%d", &x, &y);
printf("%d\n", getmax(x, y) - getmin(x, y));
}
return 0;
}
哈希
一般哈希
Hash表又被称为散列表,一般有Hash函数(散列函数)与链表结构共同实现。当我们要对若干复杂信息进行统计时,可以用Hash函数把这些复杂信息映射到一个容易维护得值域内。因为值域变简单、范围变小,有可能造成两个不同的原始信息被Hash函数映射为相同的值,所以我们需要处理这种冲突情况。
ps:离散化是一种特殊的哈希
拉链法
类似于邻接链表,开一个数组,数组的每个位置对应一个链表,查找或插入的时候,都是针对这个链表
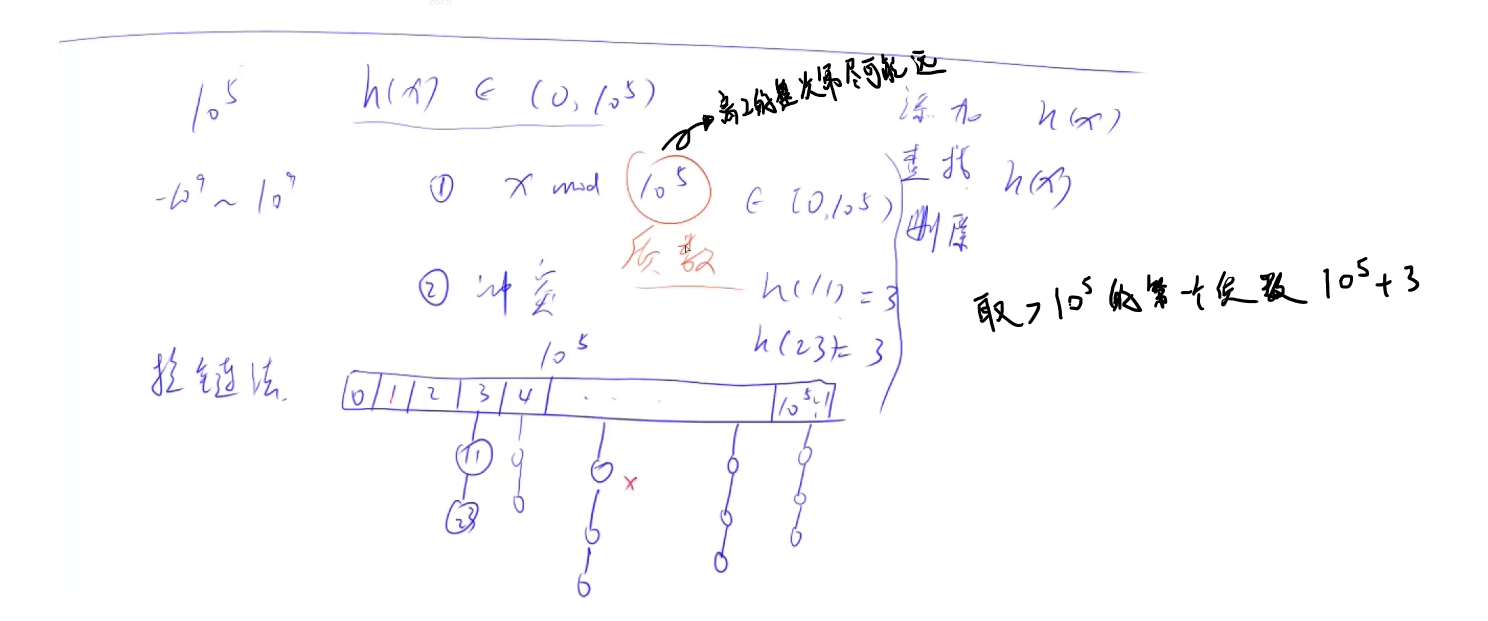
//mod为超过最大范围的第一个质数(可以避免重复,数学上有证明)
int h[mod], e[mod], ne[mod], idx;
// 向哈希表中插入一个数
void insert(int x)
{
int k = (x % mod + mod) % mod;
e[idx] = x;
ne[idx] = h[k];
h[k] = idx ++ ;
}
// 在哈希表中查询某个数是否存在
bool find(int x)
{
int k = (x % mod + mod) % mod; //此处是为了转化为正数
for (int i = h[k]; i != -1; i = ne[i])
if (e[i] == x)
return true;
return false;
}
开放寻址法
只需要开一个数组,每次找到该数应该存的位置,如果这个位置上有值,则往后寻找,直到找到一个空的位置
ps:根据经验,这个数组大小开到数据范围的2~3倍就没有问题
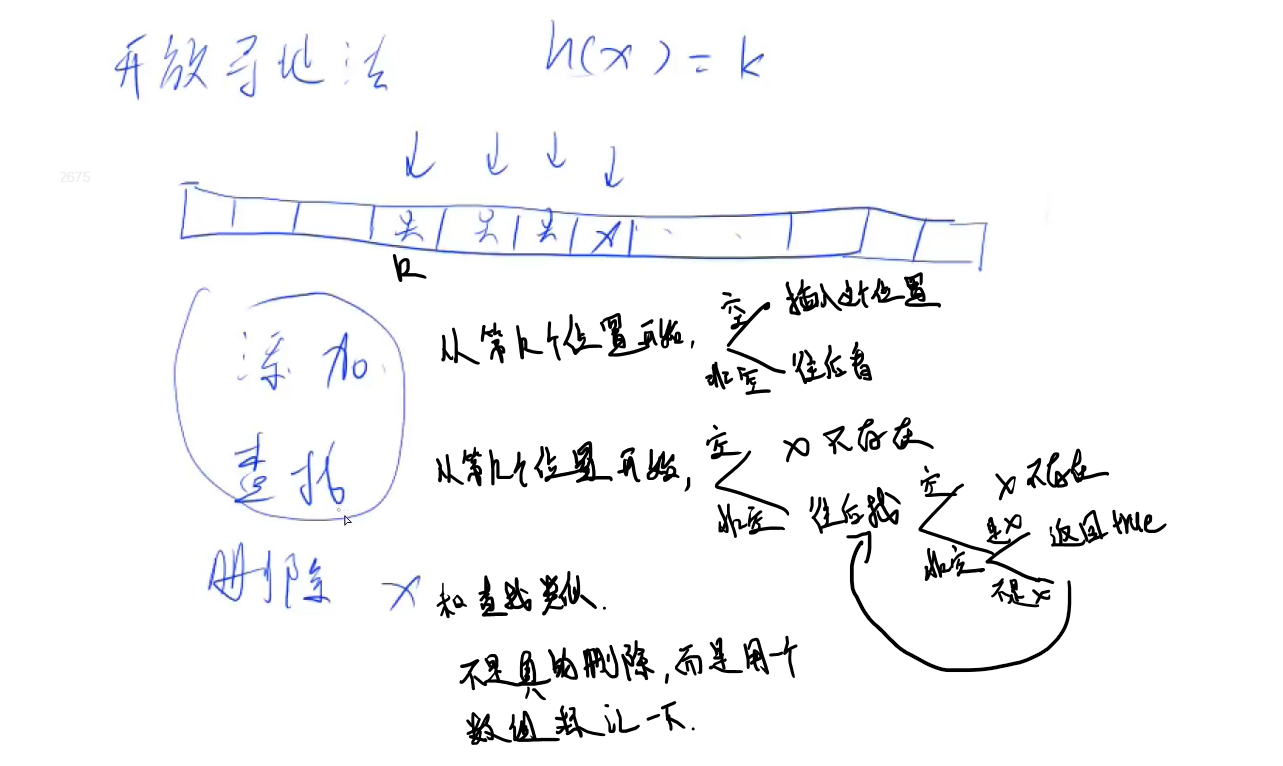
int h[mod];
// 如果x在哈希表中,返回x的下标;如果x不在哈希表中,返回x应该插入的位置
int find(int x)
{
int t = (x % mod + mod) % mod;
while (h[t] != null && h[t] != x)
{
t ++ ;
if (t == mod) t = 0;
}
return t;
}
字符串哈希
单哈希
取一固定值\(P\),把字符串看做\(P\)进制数,并分配一个大于\(0\)的数值,代表每种字符。取一固定值\(M\),求出该\(P\)进制数对\(M\)的余数,作为该字符串的\(Hash\)值。
注意:
1、需要给字符分配一个大于\(0\)的值。(比如:如果\('A'->0\),那么\('AA'->0\),这样就没法区分了)
2、通常\(P=131\)或\(13331\),\(M\)=\(2^{64}\),这种情况下\(Hash\)值产生冲突的概率极低(采用\(2^{64}\),直接使用unsigned long long自然溢出就可以)
实现模板
typedef unsigned long long ull;
ull h[maxn], p[maxn]; // h[k]存储字符串前k个字母的哈希值, p[k]存储 P^k mod 2^64
int P = 1331;
// 初始化
p[0] = 1;
for (int i = 1; i <= n; i ++ )
{
h[i] = h[i - 1] * P + str[i];
p[i] = p[i - 1] * P;
}
// 计算子串 str[l ~ r] 的哈希值
ull get(int l, int r)
{
return h[r] - h[l - 1] * p[r - l + 1];
}
双哈希
Hash冲突: Hash冲突是指两个不同的字符串映射到相同的Hash值
多值哈希: 就是有多个Hash函数,每个Hash函数的模数不一样,这样就能解决Hash冲突的问题。判断时只要其中一个Hash值不同,就认为两个字符串不同,若Hash值都相同,则认为两个字符串相同。
ps:一般来说,双值Hash就够用了
实现模板
#include <bits/stdc++.h>
using namespace std;
typedef unsigned long long ull;
const int maxn = 100010;
const int mod = 1e9 + 7;
const int base = 1331;
char s[maxn];
ull h1[maxn] = {}, h2[maxn] = {};
ull get1(int l, int r)
{
return h1[r] - h1[l-1] * p1[r - l + 1];
}
ull get2(int l, int r)
{
return (h2[r] - h2[l-1] * p2[r - l + 1] % mod + mod) % mod;
}
int main()
{
scanf("%s", s + 1);
int len = strlen(s + 1);
for(int i=1; i<=len; i++)
{
h1[i] = h1[i-1] * base + s[i];
h2[i] = (h2[i-1] * base % mod + s[i]) % mod;
}
p1[0] = 1;
p2[0] = 1;
for(int i=1; i<=100000; i++)
{
p1[i] = p1[i-1] * base;
p2[i] = p2[i-1] * base % mod;
}
//比较字符串s的[l1, r1]和[l2, r2]是否相同
int l1, r1, l2, r2;
scanf("%d%d%d%d", &l1, &r1, &l2, &r2);
//只有两次哈希值都相同才相同,只要有一次不同,那就不同
if(get1(l1, r1)==get1(l1, r1) && get2(l1, r1)==get2(l2, r2)) printf("yes");
else printf("no");
return 0;
}
例题: [POJ3461]乌力波(双哈希板子题)
#include <bits/stdc++.h>
using namespace std;
typedef unsigned long long ull;
const int maxn = 1e6 + 10;
const int base = 131, mod = 1e9 + 7;
int t = 0;
char w[maxn], s[maxn];
ull hs1[maxn] = {}, hs2[maxn] = {}, p1[maxn] = {}, p2[maxn] = {}, hw1 = 0, hw2 = 0;
ull get1(int l, int r)
{
return hs1[r] - hs1[l-1] * p1[r-l+1];
}
ull get2(int l, int r)
{
return (hs2[r] - hs2[l-1] * p2[r-l+1] % mod + mod) % mod;
}
int main()
{
scanf("%d", &t);
p1[0] = 1;
p2[0] = 1;
for(int i=1; i<=10000; i++)
{
p1[i] = p1[i-1] * base; //自然溢出
p2[i] = p2[i-1] * base % mod;
}
while(t--)
{
scanf("%s%s", w + 1, s + 1);
hw1 = hw2 = 0;
memset(hs1, 0, sizeof(hs1));
memset(hs2, 0, sizeof(hs2));
int lenw = strlen(w + 1), lens = strlen(s + 1);
for(int i=1; i<=lenw; i++)
{
hw1 = hw1 * base + w[i];
hw2 = (hw2 * base % mod + w[i]) % mod;
}
for(int i=1; i<=lens; i++)
{
hs1[i] = hs1[i-1] * base + s[i];
hs2[i] = (hs2[i-1] * base % mod + s[i]) % mod;
}
int ans = 0;
for(int l=1; l+lenw-1<=lens; l++)
{
int r = l + lenw - 1;
if(hw1 == get1(l, r) && hw2 == get2(l, r)) ans++;
}
printf("%d\n", ans);
}
return 0;
}
前缀数组
后缀 是指从某个位置 \(i\) 开始到整个串末尾结束的一个特殊子串。字符串 \(S\) 的从 \(i\) 开头的后缀表示为 \(Suffix(S,i)\),也就是 \(Suffix(S,i)=S[i..|S|-1]\)。
真后缀 指除了 \(S\) 本身的 \(S\) 的后缀。
举例来说,字符串 abcabcd 的所有后缀为 {d, cd, bcd, abcd, cabcd, bcabcd, abcabcd},而它的真后缀为 {d, cd, bcd, abcd, cabcd, bcabcd}。
前缀 是指从串首开始到某个位置 \(i\) 结束的一个特殊子串。字符串 \(S\) 的以 \(i\) 结尾的前缀表示为 \(Prefix(S,i)\),也就是 \(Prefix(S,i)=S[0..i]\)。
真前缀 指除了 \(S\) 本身的 \(S\) 的前缀。
举例来说,字符串 \(abcabcd\) 的所有前缀为 \({a, ab, abc, abca, abcab, abcabc, abcabcd}\), 而它的真前缀为 \({a, ab, abc, abca, abcab, abcabc}\)。
前缀数组定义
给定一个长度为 \(n\) 的字符串 s,其 前缀函数 被定义为一个长度为 \(n\) 的数组 \(next\)。 其中 \(next[i]\) 的定义是:
如果子串 \(s[1...i]\) 有一对相等的真前缀与真后缀:\(s[1...k]\) 和 \(s[i - k + 1 ... i]\),那么 \(next[i]\)就是这个相等的真前缀(或者真后缀,因为它们相等)的长度,也就是 \(next[i]=k\);
如果不止有一对相等的,那么 \(next[i]\) 就是其中最长的那一对的长度;
如果没有相等的,那么 \(next[i]=0\)。
简单来说 \(next[i]\) 就是,子串 \(s[0...i]\) 最长的相等的真前缀与真后缀的长度。
next[1] = 0,因为单个字符没有真前缀
ps:求前缀数组,字符串一般从1开始存(个人习惯)
举例
对于字符串 \(abcabcd\)(下标从1开始存)
\(next[1]=0\),因为 \(a\) 没有真前缀和真后缀,根据规定为 \(0\)
\(next[2]=0\),因为 \(ab\) 无相等的真前缀和真后缀
\(next[3]=0\),因为 \(abc\) 无相等的真前缀和真后缀
\(next[4]=1\),因为 \(abca\) 只有一对相等的真前缀和真后缀:\(a\),长度为 \(1\)
\(next[5]=2\),因为 \(abcab\) 相等的真前缀和真后缀只有 \(ab\),长度为 \(2\)
\(next[6]=3\),因为 \(abcabc\) 相等的真前缀和真后缀只有 \(abc\),长度为 \(3\)
\(next[7]=0\),因为 \(abcabcd\) 无相等的真前缀和真后缀
同理可以计算字符串 aabaaab 的前缀函数为 \([0, 0, 1, 0, 1, 2, 2, 3]\)。
计算过程
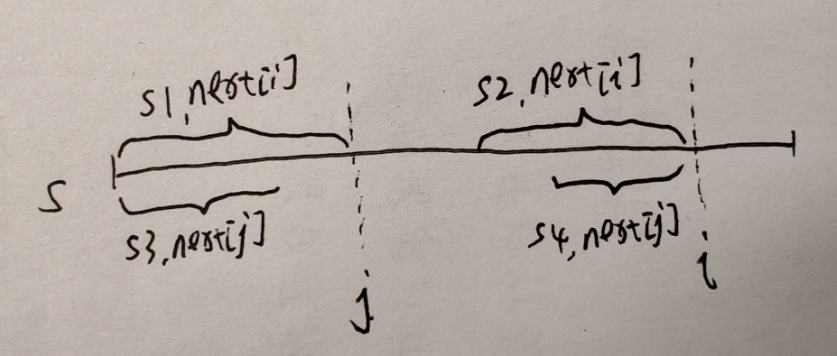
优化思想: 当已经求出了\(next[i]\)之后,此时\(j=next[i]\),效果图如上图,\(s[1,j]\)与\(s[i-j+1,i]\)相等,此时求\(i\)的下一个位置的\(next\)。
令\(i++\),然后求\(next[i]\)。
1、如果\(s[j+1]==s[i]\),则\(next[i]=j+1\),因为根据前面求的\(next\),\(s1\)和\(s2\)是相等的,只要下一个字符相等,那么就可以求出\(next[i]\)
2、如果\(s[j+1]!=s[i]\),则需要再比较前面的字符,但此时注意:我们只需要跳到\(next[j]\),然后再比较即可,因为\(s3==s4\),所以只需要令\(j=next[j]\),然后再比较\(s[j+1]\)和\(s[i]\)是否相等即可
算法模板:
// p[]是模式串,m是p的长度
求模式串的next数组:
for (int i=2, j=0; i<m; i++)
{
while(j > 0 && p[i] != p[j + 1]) j = nxt[j];
if(p[i] == p[j + 1]) j ++ ;
nxt[i] = j;
}
KMP
KMP算法思想: KMP算法,又称模式匹配算法,能够在线性时间内判定字符串\(p[1,m]\)(长度为\(m\),下标从\(1\)开始)是否为字符串\(s[1,n]\)(长度为\(n\),下标从\(1\)开始)的子串,并求出字符串\(p\)在字符串\(s\)中各次出现的位置。
算法流程:
1、对字符串\(p\)进行自我"匹配",求出其前缀数组\(next[]\)
2、对字符串\(p\)与\(s\)进行匹配,求出一个数组\(f[]\),其中\(f[i]\)表示"\(s\)中以\(i\)结尾的子串"与“\(p\)的前缀”能够匹配的最长长度,即:
f[i]=maxn{j},其中\(j<=i\)并且\(s[i-j+1,i]=p[1,j]\)
当\(f[i]==m\)时,说明\(p\)正好与\(s[i]\)的后缀匹配上,即\(p[1,m]=s[i-m+1, i]\)
优化思想:
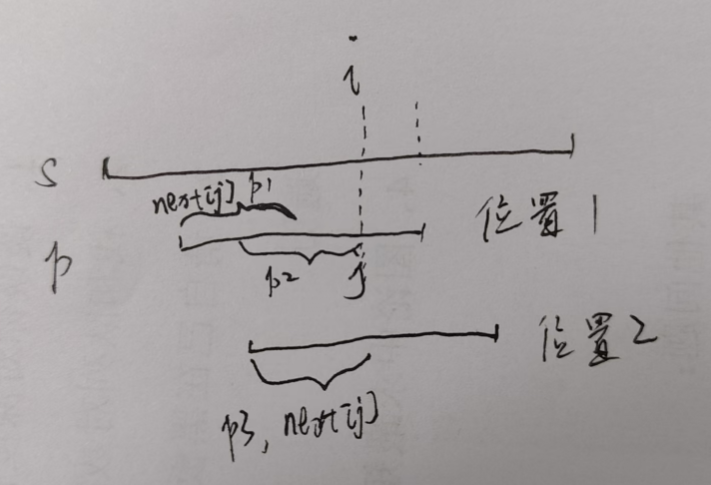
当让串\(p\)匹配串\(s\)时,假如匹配到\(s[i]\)时
此时,令\(i++\)
如果\(s[i]==p[j+1]\),则\(f[i]=j+1\),相当于在\(f[i-1]\)的基础上再扩展一个
如果\(s[i]!=p[j+1]\),则需要再跳到前面去找,按上图中,假如\(p\)在位置\(1\)时,\(f[i]=j\),当挪到位置\(2\)时,再次匹配上了,这时\(p1==p2==p3\),也就是说位置\(1\)时,\(p1\)到\(j\)的这段距离是可以跳过的,也就是直接跳到\(p1\)的位置,然后再比较\(p[j+1]\)和\(s[i]\)是否相等即可,而跳到\(p1\)的位置,就是跳\(next[j]\)
算法模板:
// s[]是长文本,p[]是模式串,n是s的长度,m是p的长度
先求模式串p的next数组:
for (int i=2, j=0; i<m; i++)
{
while(j > 0 && p[i] != p[j + 1]) j = nxt[j];
if(p[i] == p[j + 1]) j ++ ;
nxt[i] = j;
}
// 匹配
for (int i=1, j=0; i<=n; i++)
{
while(j > 0 && (j==m || s[i] != p[j+1])) j = nxt[j];
if(s[i] == p[j+1]) j++;
f[i] = j;
if(f[i] == m)
{
// 匹配成功后的逻辑
}
}
例题: [POJ3461]乌力波(kmp板子题)
#include <bits/stdc++.h>
using namespace std;
/*
kmp板子
*/
int T = 0;
char w[10010], s[1000010];
int lenw = 0, lens = 0;
int nxt[10010] = {}, f[1000010] = {};
int main()
{
scanf("%d", &T);
while(T--)
{
memset(nxt, 0, sizeof(nxt));
memset(f, 0, sizeof(f));
scanf("%s%s", w + 1, s + 1);
lenw = strlen(w + 1);
lens = strlen(s + 1);
//求前缀数组nxt
for(int i=2, j=0; i<=lenw; i++)
{
while(j > 0 && w[i] != w[j+1]) j = nxt[j];
if(w[i] == w[j+1]) j++;
nxt[i] = j;
}
//kmp算法
int ans = 0;
for(int i=1, j=0; i<=lens; i++)
{
while(j > 0 && (j == lenw || s[i] != w[j+1])) j = nxt[j];
if(s[i] == w[j+1]) j++;
f[i] = j;
//匹配长度为lenw时,说明出现了一次,累加答案
if(f[i] == lenw) ans++;
}
printf("%d\n", ans);
}
return 0;
}
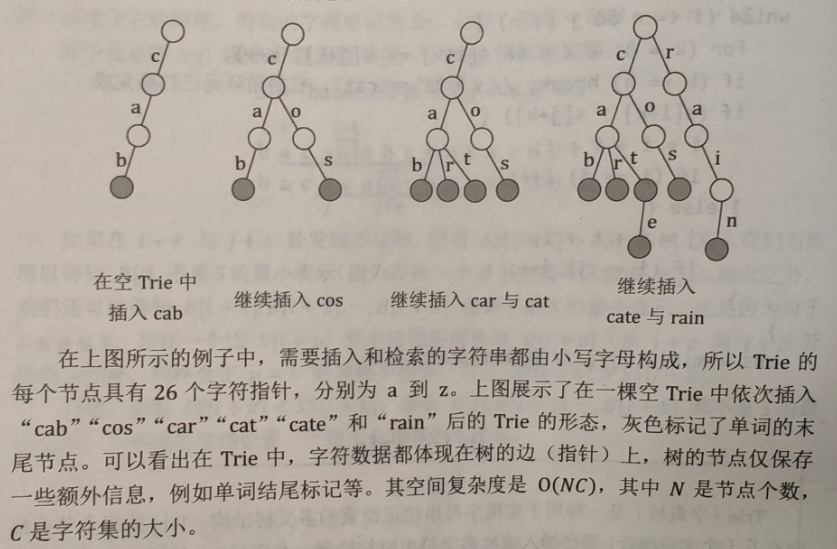
Trie树
\(Trie\)(字典树)是一种用于实现字符串快速检索的多叉树结构。
\(Trie\)的每个节点都拥有若干个字符指针,若在插入或检索字符串时扫描到一个字符\(c\),就沿着当前节点的\(c\)字符指针,走向该指针指向的节点
ps:每个节点不存储具体的信息,而是存储对应的指针
空间复杂度为\(O(nc)\),其中\(N\)是节点个数,\(C\)是字符集的大小。
主要有两个操作:插入和查询
插入
当需要插入一个字符串\(S\)时,我们令一个指针\(P\)起初指向根节点。然后,一次扫描\(S\)中的每个字符\(c\)
1、若\(P\)的\(c\)字符指针指向一个已经存在的节点\(Q\),则令\(P=Q\)
2、若\(P\)的\(c\)字符指针直向空,则新建一个节点\(Q\),令\(P\)的\(c\)字符指针指向\(Q\),然后令\(P=Q\)
查询
当需要检索一个字符串\(S\)在\(Trie\)中是否存在时,我们令一个指针\(P\)起初指向根节点,然后扫描\(S\)中的每个字符\(c\)
1、若\(P\)的\(c\)字符指针指向空,则说明\(S\)没有被插入过\(Trie\),结束检索
2、若\(P\)的\(c\)字符指针指向一个已经存在的节点\(Q\),则令\(P=Q\)
ps:在建\(Trie\)树时,可以维护其他信息,比如:结束节点,数量等
代码模板
int Trie[maxn][26] = {}, tot = 1, end[maxn*26] = {}; //初始化,假设字符串由小写字母构成
void insert(char str[]) //插入一个字符串
{
int len = strlen(str), p = 1;
for(int i=0; i<len; i++)
{
int ch = str[i] - 'a';
if(Trie[p][ch] == 0) Trie[p][ch] = ++tot;
p = Trie[p][ch];
}
end[p] = true;
}
bool search(char str[]) //检索字符串是否存在
{
int len = strlen(str), p = 1;
for(int i=0; i<len; i++)
{
p = Trie[p][str[i] - 'a'];
if(p == 0) return false
}
return end[p];
}
分块/莫队
分块
简介
分块是一种思想,而不是一种数据结构
基本思想: 通过对原数据的适当划分,并在划分后的每一块上预处理部分信息,从而较一般的暴力算法取得更优的时间复杂度,因此分块也被称为优雅地暴力
时间复杂度:
- 分块的时间复杂度主要取决于分块的块长,一般可以通过均值不等式求出某个问题下的最优块长,以及相应的时间复杂度
- 块的大小为b,当\(b = \sqrt{n}\)时,单次操作的时间复杂度最优,为\(O(\sqrt{n})\),总时间复杂度为\(O(m*\sqrt{n})\)
优点: 分块是一种很灵活的思想,实现起来也比较简单,相较于树状数组和线段树,分块的优点是通用性更好,可以维护很多树状数组和线段树无法维护的信息。
缺点: 一般情况下时间复杂度比线段树和树状数组要高
例题
例题: 5939.一个简单的整数问题
https://h.hszxoj.com/d/hztg/p/HZTG5939
分析: 将序列按每\(s\)个元素一块进行分块,并记录每块的区间和\(b_i\)
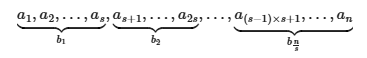
最后一个块可能是不完整的(因为\(n\)很可能不是\(s\)的倍数),不影响分析
查询:
- 若\(l\)和\(r\)在同一个块内,直接暴力求和即可,因为块长为\(s\),因此最坏的复杂度为\(O(s)\)
- 若\(l\)和\(r\)不在同一个块内,则答案由三部分组成:以\(l\)开头的不完整块,中间几个完整块,以\(r\)结尾的不完整块。对于不完整块,直接暴力计算,对于完整块,直接利用已经求出的\(b_i\)求和即可。最坏时间复杂度为\(O(n/s+s)\)
修改:
- 若\(l\)和\(r\)在同一个块内,直接暴力修改即可,因为块长为\(s\),因此最坏的复杂度为\(O(s)\)
- 若\(l\)和\(r\)不在同一个块内,则需要修改三部分:以\(l\)开头的不完整块,中间几个完整块,以\(r\)结尾的不完整块。对于不完整块,直接暴力修改,对于完整块,直接修改\(b_i\)即可。最坏时间复杂度为\(O(n/s+s)\)
利用均值不等式可知,当\(n/s == s\)时,即 \(s = \sqrt{n}\)时,单次操作的时间复杂度最优,为\(O(\sqrt{n})\)
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 1e5 + 10;
int n = 0, m = 0;
int a[maxn] = {};
//L[i]和R[i]表示第i段的左右端点,pos[i]表示a序列中的第i个位置的数位于第几段
//cnt表示分成的段数
int L[400] = {}, R[400] = {}, pos[maxn] = {}, cnt;
ll sum[400] = {}, add[400] = {};
//分块
void init()
{
cnt = sqrt(n);
for(int i=1; i<=cnt; i++)
{
L[i] = (i-1) * cnt + 1;
R[i] = i * cnt;
}
//分出sqrt(n)块后,还有剩余的部分,单独再分一块
if(R[cnt] < n)
{
cnt++;
L[cnt] = R[cnt-1] + 1;
R[cnt] = n;
}
//预处理pos和sum
for(int i=1; i<=cnt; i++)
{
for(int j=L[i]; j<=R[i]; j++)
{
pos[j] = i;
sum[i] += a[j];
}
}
}
ll Query(int l, int r)
{
ll ans = 0;
int p = pos[l], q = pos[r];
if(p == q)//l~r处于同一分块中
{
for(int i=l; i<=r; i++) ans += a[i];
ans += (r - l + 1) * add[p];
}
else
{
//先处理整块数据
for(int i=p+1; i<q; i++)
{
ans += sum[i] + add[i] * (R[i] - L[i] + 1);
}
//处理最左边块
for(int i=l; i<=R[p]; i++) ans += a[i];
ans += (R[p] - l + 1) * add[p];
//处理最右边块
for(int i=L[q]; i<=r; i++) ans += a[i];
ans += (r - L[q] + 1) * add[q];
}
return ans;
}
void Update(int l, int r, int d)
{
int p = pos[l], q = pos[r];
if(p == q)//l~r处于同一分块中
{
for(int i=l; i<=r; i++) a[i] += d;
sum[p] += d * (r - l + 1);
}
else
{
//先处理整块数据
for(int i=p+1; i<q; i++) add[i] += d;
//处理最左边块
for(int i=l; i<=R[p]; i++) a[i] += d;
sum[p] += d * (R[p] - l + 1);
//处理最右边块
for(int i=L[q]; i<=r; i++) a[i] += d;
sum[q] += d * (r - L[q] + 1);
}
}
int main()
{
char op[3] = {};
int l = 0, r = 0, d = 0;
scanf("%d%d", &n, &m);
for(int i=1; i<=n; i++) scanf("%d", &a[i]);
init();
//指令
while(m--)
{
scanf("%s", op);
if(op[0] == 'Q')
{
scanf("%d%d", &l, &r);
ll ans = Query(l, r);
printf("%lld\n", ans);
}
else
{
scanf("%d%d%d", &l, &r, &d);
Update(l, r, d);
}
}
return 0;
}
莫队
莫队:莫涛归纳总结的一种解决区间查询等问题的离线算法,基于分块思想。
朴素版
对于序列上的区间询问问题(序列长度为\(n\),询问为\(m\)),如果可以在\(O(1)\)内从\([l, r]\)的答案扩展到\([l-1, r],[l+1, r],[l, r-1],[l, r+1]\)(即与\([l, r]\)相邻的区间)的答案,可以考虑使用莫队算法来解决问题。
例题: 1648.HH的项链
https://h.hszxoj.com/d/hztg/p/HZTG1648?tid=67877d8357cd8663ca471038
从\([l, r]\)移动到\([l-1, r]\)相当于增加\(a[l]\)的值,时间复杂度\(O(1)\)
从\([l, r]\)移动到\([l+1, r]\)相当于减去\(a[l]\)的值,时间复杂度\(O(1)\)
所以该题可以用莫队算法,每次询问的移动的时间复杂度为\(O(n)\),总时间复杂度为\(O(mn)\)
#include <bits/stdc++.h>
using namespace std;
const int maxn = 50010;
const int maxx = 1e6+10;
int n = 0, m = 0;
int a[maxn] = {};
int l = 1, r = 0, cnt[maxx] = {}, ans = 0;
void add(int x)
{
if(cnt[x] == 0) ans++;
cnt[x]++;
}
void del(int x)
{
cnt[x]--;
if(cnt[x] == 0) ans--;
}
int main()
{
int x = 0, y = 0;
scanf("%d", &n);
for(int i=1; i<=n; i++) scanf("%d", &a[i]);
scanf("%d", &m);
while(m--)
{
scanf("%d%d", &x, &y);
//莫队算法
while(x<l) { l--; add(a[l]); }
while(x>l) { del(a[l]); l++; }
while(y<r) { del(a[r]); r--; }
while(y>r) { r++; add(a[r]); }
printf("%d\n", ans);
}
return 0;
}
分块排序版
- 对原序列进行分块,先按左端点所在块由小到大排序,再按右端点由小到大排序
时间复杂度:
假设m为操作数,B为块大小。考虑对于一个块内的l,其r是单增的,于是考虑如下:
- 左端点,在块内可能会一前一后这样设置,这样复杂度被卡到最满,为O(m*B)
- 右端点,考虑各块内的询问,显然都可以做到单块O(n),所以不需要考虑m的贡献,即右端点移动的复杂度就是\(\frac{n}{B} \cdot n = \frac{n^2}{B}\)
- 总的时间复杂度为\(O(m*b + \frac{n}{B} \cdot n = \frac{n^2}{B})\)
均值一下发现\(m \cdot B + \frac{n^2}{B} \geq 2\sqrt{n^2 m} = O(n\sqrt{m})\),此时有 \(m \cdot B = \frac{n^2}{B}\),解得 \(B = \frac{n}{\sqrt{m}}\)。
所以取块的大小为\(\frac{n}{\sqrt{m}}\)时达到理论最优,复杂度为\(O(n\sqrt{m})\)
例题: 1648.HH的项链
https://h.hszxoj.com/d/hztg/p/HZTG1648?tid=67877d8357cd8663ca471038
#include <bits/stdc++.h>
using namespace std;
const int maxn = 50010;
const int maxx = 1e6+10;
const int maxm = 2e5 + 10;
int n = 0, m = 0;
int a[maxn] = {};
int l = 1, r = 0, col[maxx] = {}, num = 0, ans[maxm] = {};
int L[maxn] = {}, R[maxn] = {}, pos[maxn] = {}, cnt = 0;
struct node
{
int x, y, id;
}q[maxm];
bool cmp(node &nd1, node &nd2)
{
int p = pos[nd1.x], q = pos[nd2.x];
if(p == q) return nd1.y < nd2.y;
return p < q;
}
void init()
{
int B = n / sqrt(m);
cnt = n / B;
for(int i=1; i<=cnt; i++)
{
L[i] = n / cnt * (i - 1) + 1;
R[i] = n / cnt * i;
}
if(R[cnt] < n)
{
cnt++;
L[cnt] = R[cnt-1] + 1;
R[cnt] = n;
}
for(int i=1; i<=cnt; i++)
{
for(int j=L[i]; j<=R[i]; j++)
{
pos[j] = i;
}
}
}
void add(int x)
{
if(col[x] == 0) num++;
col[x]++;
}
void del(int x)
{
col[x]--;
if(col[x] == 0) num--;
}
int main()
{
int x = 0, y = 0;
scanf("%d", &n);
for(int i=1; i<=n; i++) scanf("%d", &a[i]);
//分块
init();
scanf("%d", &m);
for(int i=1; i<=m; i++)
{
scanf("%d%d", &x, &y);
q[i] = { x, y, i };
}
sort(q+1, q+1+m, cmp);
for(int i=1; i<=m; i++)
{
x = q[i].x;
y = q[i].y;
//莫队算法
while(x<l) { l--; add(a[l]); }
while(x>l) { del(a[l]); l++; }
while(y<r) { del(a[r]); r--; }
while(y>r) { r++; add(a[r]); }
ans[q[i].id] = num;
}
for(int i=1; i<=m; i++) printf("%d\n", ans[i]);
return 0;
}
奇偶排序版
奇偶排序是对上述分块排序算法的优化
看下面这组数据:
//设块的大小为2(假设)
1 1
2 100
3 1
4 100
手动模拟一下就可以发现,\(r\)指针移动次数大概为\(300\)次,先从\(1\)移动到\(100\),再移动到\(1\),再移动到\(100\)
优化:
对于奇数块的询问,\(r\)按从小到大排序,偶数块的询问,\(r\)按从大到小排序,这样我们的\(r\)指针在处理完奇数块的问题后,将在返回的途中处理偶数块的问题,再向\(n\)移动处理下一个奇数块的问题,优化了\(r\)指针的移动次数。
一般情况下,这种优化能让程序快\(30\%\)左右
例题: 1648.HH的项链
https://h.hszxoj.com/d/hztg/p/HZTG1648?tid=67877d8357cd8663ca471038
#include <bits/stdc++.h>
using namespace std;
const int maxn = 50010;
const int maxx = 1e6+10;
const int maxm = 2e5 + 10;
int n = 0, m = 0;
int a[maxn] = {};
//莫队信息
int l = 1, r = 0, col[maxx] = {}, num = 0, ans[maxm] = {};
//分块信息
int L[maxn] = {}, R[maxn] = {}, pos[maxn] = {}, cnt = 0;
struct node
{
int x, y, id;
}q[maxm];
//奇偶排序
//左端点按所在块,由小到大排序
//奇数块时右端点由小到大,偶数块右端点由大到小
//奇偶排序可以做到上一块r由1~n,该块r由n~1
bool cmp(node &nd1, node &nd2)
{
int p = pos[nd1.x], q = pos[nd2.x];
if(p != q) return p < q;
if(p & 1 == 1) return nd1.y < nd2.y;
else return nd1.y > nd2.y;
}
void init()
{
//当块的大小取n/sqrt(m)时,时间复杂度可以达到最优
int B = n / sqrt(m);
cnt = n / B;
for(int i=1; i<=cnt; i++)
{
L[i] = B * (i - 1) + 1;
R[i] = B * i;
}
if(R[cnt] < n)
{
cnt++;
L[cnt] = R[cnt-1] + 1;
R[cnt] = n;
}
for(int i=1; i<=cnt; i++)
{
for(int j=L[i]; j<=R[i]; j++)
{
pos[j] = i;
}
}
}
void add(int x)
{
if(col[x] == 0) num++;
col[x]++;
}
void del(int x)
{
col[x]--;
if(col[x] == 0) num--;
}
int main()
{
int x = 0, y = 0;
scanf("%d", &n);
for(int i=1; i<=n; i++) scanf("%d", &a[i]);
//分块
scanf("%d", &m);
init();
for(int i=1; i<=m; i++)
{
scanf("%d%d", &x, &y);
q[i] = { x, y, i };
}
sort(q+1, q+1+m, cmp);
for(int i=1; i<=m; i++)
{
x = q[i].x;
y = q[i].y;
//莫队算法
while(x<l) { l--; add(a[l]); }
while(x>l) { del(a[l]); l++; }
while(y<r) { del(a[r]); r--; }
while(y>r) { r++; add(a[r]); }
ans[q[i].id] = num;
}
for(int i=1; i<=m; i++) printf("%d\n", ans[i]);
return 0;
}
带修莫队
带修莫队是一种支持单点修改的莫队算法。
普通莫队是不能带修改的,我们可以强行让他可以修改,就像\(DP\)一样,可以强行加上一维时间维,表示这次操作的时间
即把询问\([l, r]\)变成\([l, r, time]\)。
那么我们的坐标也可以在时间维上移动,即\([l, r, time]\)多了一维可以移动的方向,变成:
- \([l-1, r, time]\)
- \([l+1, r, time]\)
- \([l, r-1, time]\)
- \([l, r+1, time]\)
- \([l, r, time-1]\)
- \([l, r, time+1]\)
这样的转移也是\(O(1)\)的,但是排序多了一个关键字
算法简介:
还是对询问进行排序,每个询问除了左端点和右端点,还要记录这次询问是在第几次修改之后(时间),以左端点所在块为第一关键字,右端点所在块为第二关键字,时间为第三关键字进行排序
暴力查询时,如果当前修改数比询问的修改数少,就把没修改的进行修改,反之回退
需要注意的是,修改分为两部分:
- 若修改的位置在当前区间内,需要更新答案(del原颜色,add修改后的颜色)
- 无论修改的位置是否在当前区间内,都要进行修改(以供add和del函数在以后更新答案)
分块大小为\(n^{2/3}\),分成\(n^{1/3}\)块,此时时间复杂度最低,证明见\(oi-wiki\)
例题: 351.维护队列
https://h.hszxoj.com/d/hztg/p/HZTG351?tid=67877d8357cd8663ca471038
#include <bits/stdc++.h>
using namespace std;
const int maxn = 150010;
const int maxx = 1e6+10;
const int maxm = 150010;
//带修莫队,相当于在朴素莫队的基础上,增加了一维,表示时间
//在完成朴素莫队更新后,还要判断修改时间,将修改时间更新到正确位置
int n = 0, m = 0;
int a[maxn] = {};
//莫队数据
int l = 1, r = 0, t = 0, col[maxx] = {}, num = 0, ans[maxm] = {};
//分块数据
int L[500] = {}, R[500] = {}, pos[maxn] = {}, cnt = 0;
struct node1
{
//t表示该询问位于第几次修改
int id, l, r, t;
}q[maxm] = {};
//存储修改信息
struct node2
{
int x, c;
}rp[maxm] = {};
bool cmp(const node1 &nd1, const node1 &nd2)
{
//先按左端点所在块升序
//左端点块相同按右端点所在块升序
//左右端点块相同,按t升序
int p = pos[nd1.l], q = pos[nd2.l];
if(p != q) return p < q;
p = pos[nd1.r], q = pos[nd2.r];
if(p != q) return p < q;
return nd1.t < nd2.t;
}
//分块
void init()
{
int B = pow(n, 0.666);
cnt = n / B;
for(int i=1; i<=cnt; i++)
{
L[i] = (i-1) * B + 1;
R[i] = i * B;
}
if(R[cnt] < n)
{
cnt++;
L[cnt] = R[cnt-1] + 1;
R[cnt] = n;
}
for(int i=1; i<=cnt; i++)
{
for(int j=L[i]; j<=R[i]; j++)
{
pos[j] = i;
}
}
}
//朴素莫队加
void add(int x)
{
if(col[x] == 0) num++;
col[x]++;
}
//朴素莫队减
void del(int x)
{
col[x]--;
if(col[x] == 0) num--;
}
int main()
{
char op[3] = {};
int x = 0, y = 0;
int mq = 0, mr = 0;
scanf("%d%d", &n, &m);
for(int i=1; i<=n; i++) scanf("%d", &a[i]);
for(int i=1; i<=m; i++)
{
scanf("%s%d%d", op, &x, &y);
if(op[0] == 'Q') //单独记录查询的信息
{
mq++;
q[mq] = { mq, x, y, mr };
}
else //单独记录修改的信息
{
mr++;
rp[mr] = { x, y };
}
}
init();
sort(q+1, q+1+mq, cmp);
for(int i=1; i<=mq; i++)
{
//朴素莫队操作
while(q[i].l<l) { l--; add(a[l]); }
while(q[i].l>l) { del(a[l]); l++; }
while(q[i].r<r) { del(a[r]); r--; }
while(q[i].r>r) { r++; add(a[r]); }
//更新时间t这一维
while(q[i].t<t)
{
//修改的数据位于[l,r]之间,则需要更新,否则不需要更新
if(rp[t].x>=l && rp[t].x<=r)
{
del(a[rp[t].x]);
add(rp[t].c);
}
//注意这里是交换值,不是直接更改a数组,因为后面还要回滚
swap(a[rp[t].x], rp[t].c);
t--;
}
while(q[i].t>t)
{
t++;
if(rp[t].x>=l && rp[t].x<=r)
{
del(a[rp[t].x]);
add(rp[t].c);
}
swap(a[rp[t].x], rp[t].c);
}
ans[q[i].id] = num;
}
for(int i=1; i<=mq; i++) printf("%d\n", ans[i]);
return 0;
}
回滚莫队
引入:
- 有些题目在区间转移时,可能会出现增加或者删除无法实现的问题。在只有增加不可实现或者只有删除不可实现的时候,就可以使用回滚莫队在\(O(n\sqrt{m})\)的时间内解决问题。
- 回滚莫队分为只使用增加操作的回滚莫队和只使用删除操作的回滚莫队。
核心思想:
既然只能实现一个操作,那么就只使用一个操作,剩下的交给回滚莫队
复杂度证明:
假设回滚莫队的分块大小是\(b\):
- 对于左、右端点在同一个块内的询问,可以在\(O(b)\)时间内计算
- 对于其他询问,考虑左端点在相同块内的询问,他们的右端点单调递增,移动右端点的时间复杂度是\(O(n)\),而左端点单次询问的移动不超过\(b\),因为有\(\frac{n}{b}\)个块,所以总复杂度是\(O\left(mb + \frac{n^2}{b}\right)\),取\(b = \frac{n}{\sqrt{m}}\)最优,时间复杂度为\(O(n\sqrt{m})\)
块大小\(b\),当\(b = \frac{n}{\sqrt{m}}\)最优,时间复杂度为\(O(n\sqrt{m})\)
例题: 605 permu
https://h.hszxoj.com/d/hztg/p/HZTG605?tid=67877d8357cd8663ca471038
#include <bits/stdc++.h>
using namespace std;
const int maxn = 50010;
const int maxm = 50010;
int n = 0, m = 0;
int a[maxn] = {};
//分块信息
int L[300] = {}, R[300] = {}, pos[maxn] = {}, cnt = 0;
struct node
{
int id, l, r;
}q[maxm];
//ls[x]和rs[x]分别表示x点向左向右延伸距离
//backls, backrs用于后面的回滚
int ls[maxn] = {}, rs[maxn] = {}, backls[maxn] = {}, backrs[maxn] = {}, num = 0, ans[maxm] = {};
bool cmp(const node &nd1, const node &nd2)
{
int p = pos[nd1.l], q = pos[nd2.l];
if(p != q) return p < q;
return nd1.r < nd2.r;
}
void init()
{
int B = n / sqrt(m);
cnt = n / B;
for(int i=1; i<=cnt; i++)
{
L[i] = (i-1) * B + 1;
R[i] = i * B;
}
if(R[cnt] < n)
{
cnt++;
L[cnt] = R[cnt-1] + 1;
R[cnt] = n;
}
for(int i=1; i<=cnt; i++)
{
for(int j=L[i]; j<=R[i]; j++)
{
pos[j] = i;
}
}
}
void add(int x)
{
//更新x这个点的左右延伸距离
//如果x在某个连续区间的中间位置,可能会出现左延伸或右延伸不能更新,这种情况不影响答案
//因为我们求的是最大连续区间,所以只要保证当x为连续区间边界的点时,能够更新就可以
//因此,后面我们要更新rs[x-ls[x]+1]和ls[x+rs[x]-1]的值
ls[x] = ls[x-1] + 1; //左边延伸+1
rs[x] = rs[x+1] + 1; //右边延伸+1;
int t = ls[x] + rs[x] - 1;
//更新该连续区间左右端点的延伸距离
rs[x-ls[x]+1] = t;
ls[x+rs[x]-1] = t;
num = max(num, t);
}
int main()
{
int x = 0, y = 0;
scanf("%d%d", &n, &m);
for(int i=1; i<=n; i++)
{
scanf("%d", &a[i]);
}
for(int i=1; i<=m; i++)
{
scanf("%d%d", &x, &y);
q[i] = { i, x, y };
}
init();
sort(q+1, q+1+m, cmp);
for(int i=1; i<=m; )
{
int j = i;
while(j<=m && pos[q[i].l] == pos[q[j].l]) j++;
int right = R[pos[q[i].l]];
//块内移动,直接暴力
while(i<j && q[i].r<=right)
{
num = 0;
memset(ls, 0, sizeof(ls));
memset(rs, 0, sizeof(rs));
int id = q[i].id, l = q[i].l, r = q[i].r;
for(int k=l; k<=r; k++) add(a[k]);
ans[q[i].id] = num;
i++;
}
//块外移动
//r设置为q[i].l所在块终点位置,然后向右移动
//l设置为r+1,即q[i].l所在块的下一个块的起始位置,以保证初始空间为0,然后向左移动
//r的轨迹会一直往后移(前面对q的排序)
//l会在q[i].l中不断来回移动
//每次求出一个询问后,回滚到l的起始位置
num = 0;
memset(ls, 0, sizeof(ls));
memset(rs, 0, sizeof(rs));
int r = right, l = right + 1;
while(i < j)
{
//先向右扩展
while(r < q[i].r) { r++; add(a[r]); }
//先备份下来,以便后面回滚,然后再向左扩展
int backup = num;
memcpy(backls, ls, sizeof(ls));
memcpy(backrs, rs, sizeof(rs));
while(l > q[i].l) { l--; add(a[l]); }
ans[q[i].id] = num;
//回滚
l = right + 1;
num = backup;
memcpy(ls, backls, sizeof(ls));
memcpy(rs, backrs, sizeof(rs));
i++;
}
num = 0;
memset(ls, 0, sizeof(ls));
memset(rs, 0, sizeof(rs));
}
for(int i=1; i<=m; i++) printf("%d\n", ans[i]);
return 0;
}
平衡树
splay
#include <bits/stdc++.h>
using namespace std;
const int maxn = 100005;
//rt:根节点编号,tot:节点个数,fa[i]:父亲
//ch[i][0]左儿子编号,ch[i][1]右儿子编号
//val[i]节点权值,cnt[i]权值出现次数,sz[i]子树大小
int rt, tot, fa[maxn], ch[maxn][2], val[maxn], cnt[maxn], sz[maxn];
struct Splay
{
//在改变节点位置后,将节点x的size更新
void maintain(int x)
{
sz[x] = sz[ch[x][0]] + sz[ch[x][1]] + cnt[x];
}
//判断节点x是父亲节点的左儿子还是右儿子
//左儿子返回false,右儿子返回true
bool get(int x)
{
return x == ch[fa[x]][1];
}
//销毁节点x
void clear(int x)
{
ch[x][0] = ch[x][1] = fa[x] = val[x] = cnt[x] = 0;
}
//为了使splay保持平衡而进行旋转操作,
//旋转的本质是将某个节点上移一个位置
void rotate(int x)
{
int y = fa[x], z = fa[y], chk = get(x);
ch[y][chk] = ch[x][chk^1];
if(ch[x][chk^1]) fa[ch[x][chk^1]] = y;
ch[x][chk^1] = y;
fa[y] = x;
fa[x] = z;
if(z) ch[z][y==ch[z][1]] = x;
maintain(y);
maintain(x);
}
void splay(int x)
{
for(int f=fa[x]; f=fa[x], f; rotate(x))
{
if(fa[f])
{
rotate(get(x) == get(f) ? f : x);
}
}
rt = x;
}
void ins(int k)
{
if(!rt)
{
val[++tot] = k;
cnt[tot]++;
rt = tot;
maintain(rt);
return;
}
int cur = rt, f = 0;
while(1)
{
if(val[cur] == k)
{
cnt[cur]++;
maintain(cur);
maintain(f);
splay(cur);
break;
}
f = cur;
cur = ch[cur][val[cur] < k];
if(!cur)
{
val[++tot] = k;
cnt[tot]++;
fa[tot] = f;
ch[f][val[f] < k] = tot;
maintain(tot);
maintain(f);
splay(tot);
break;
}
}
}
//查询 x 的排名
int rk(int k)
{
int res = 0, cur = rt;
while(1)
{
if(k < val[cur])
{
cur = ch[cur][0];
}
else
{
res += sz[ch[cur][0]];
if(!cur) return res + 1;
if(k == val[cur])
{
splay(cur);
return res + 1;
}
res += cnt[cur];
cur = ch[cur][1];
}
}
}
//查询排名 x 的数
int kth(int k)
{
int cur = rt;
while(1)
{
if(ch[cur][0] && k<=sz[ch[cur][0]])
{
cur = ch[cur][0];
}
else
{
k -= cnt[cur] + sz[ch[cur][0]];
if(k <= 0)
{
splay(cur);
return val[cur];
}
cur = ch[cur][1];
}
}
}
//将 x 插入(此时 x 已经在根的位置了),
//前驱即为 x 的左子树中最右边的节点,最后将 x 删除即可。
//在进行pre之前,先要ins(x)
int pre()
{
int cur = ch[rt][0];
if(!cur) return cur;
while(ch[cur][1]) cur = ch[cur][1];
splay(cur);
return cur;
}
int nxt()
{
int cur = ch[rt][1];
if(!cur) return cur;
while(ch[cur][0]) cur = ch[cur][0];
splay(cur);
return cur;
}
void del(int k)
{
rk(k);
if(cnt[rt] > 1)
{
cnt[rt]--;
maintain(rt);
return;
}
if(!ch[rt][0] && !ch[rt][1])
{
clear(rt);
rt = 0;
return;
}
if(!ch[rt][0])
{
int cur = rt;
rt = ch[rt][1];
fa[rt] = 0;
clear(cur);
return;
}
if(!ch[rt][1])
{
int cur = rt;
rt = ch[rt][0];
fa[rt] = 0;
clear(cur);
return;
}
int cur = rt;
int x = pre();
fa[ch[cur][1]] = x;
ch[x][1] = ch[cur][1];
clear(cur);
maintain(rt);
}
}tree;
int main()
{
int n = 0, opt = 0, x = 0;
scanf("%d", &n);
for(int i=1; i<=n; i++)
{
scanf("%d%d", &opt, &x);
if(opt == 1)
{
tree.ins(x);
}
else if(opt == 2)
{
tree.del(x);
}
else if(opt == 3)
{
printf("%d\n", tree.rk(x));
}
else if(opt == 4)
{
printf("%d\n", tree.kth(x));
}
else if(opt == 5)
{
tree.ins(x);
printf("%d\n", val[tree.pre()]);
tree.del(x);
}
else if(opt == 6)
{
tree.ins(x);
printf("%d\n", val[tree.nxt()]);
tree.del(x);
}
}
return 0;
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号