2024.8.7

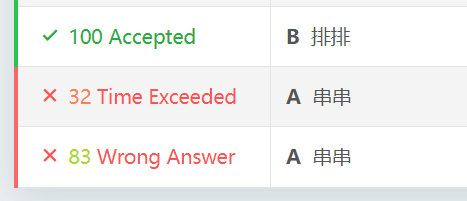
如你所见，\(32+100+20+13\)。那个 \(83\) 是没特判 \(n=1\)。

T1 串串

题意：给一个字符串，说这个串是把一个串反转好多次后得到的前缀，求原串的可能长度。

先 \(Hash\)，然后跑。嫌 string 慢然后用了char，然后因为不习惯调了半天。其实我做的时候只反转了一次，就可以通过所有数据了，甚至原题也可以，数据太水，我随手一个 \(hack\) 把我干掉了，但是其他人都没 \(hack\) 掉。

换了个做法，就是枚举原串长度然后倍增去匹配，复杂度上界是 \(O(|S|\log|S|)\) 的，理论上跑不满，但是学校上 \(T\) 了，原题却能过。

哦哦我发现了，我没预处理 \(P\) 的幂次！天然带一个 \(\log\)。

const int N = 1e6+5;
const int P = 1331;
int h1[N],h2[N];
int qp(int a,int b)
{
	int res{1};
	while(b){if(b&1) res *= a;a*=a;b>>=1;}
	return res;
}
inline int getH1(int l,int r){return h1[r] - h1[l-1] * qp(P,r-l+1);}
inline int getH2(int l,int r){return h2[r] - h2[l-1] * qp(P,r-l+1);}
inline bool dfs(int now,int len)
{
	len = min(len,n-now+1);
	if(now+len-1 == n){if(getH1(now,now+len-1) == getH2(n+1-now,n+1-(now-len+1))) return true;return false;}
	if(getH1(now,now+len-1) == getH2(n+1-now,n+1-(now-len+1))) return dfs(now+len-1,now+len-1);return false;
}
char s[N];
signed main()
{
	#ifdef LOCAL
	freopen("in.in","r",stdin);
//	freopen("out.out","w",stdout);
	#endif
	cin.tie(0),cout.tie(0);
	int T = read();
	while(T--)
	{
		scanf("%s",s+1);
		n = strlen(s+1);
		for(int i{1};i<=n;i++) h1[i] = h1[i-1] * P + s[i]-'a';
		for(int i{1};i<=n;i++) h2[i] = h2[i-1] * P + s[n-i+1]-'a';
		for(int i{2};i<n;i++)
		{
			int len = min(i,n-i+1);
			if(getH1(i-len+1,i) == getH2(n-i-len+2,n+1-i) && dfs(i+len-1,i+len-1)) writek(i);
		}
		write(n);putchar(10);
	}
}

T2 排排

题意：给定 \(1 \sim n\) 的排列 \(P\)，每次操作选一个位置，前面递增排，后面递增排，问最少几次能使排列单调递增。

显然答案很小。一般情况下（假设 \(1\) 不在排列末位），我把最后一位定住，排前面，那样 \(1\) 就到位了，然后我再把 \(1\) 定住，排后面，就全好了。所以一般情况只需要 \(2\) 次就够了。

那当然考虑些特殊情况：\(0\) 次，天然单调递增。\(1\) 次，定一个位置后，前面一换后面一换刚好到位，说明 \(P_i=i\)，且 \(1 \sim i-1\) 的数都在它前面，剩下的数都在它后面，排一次就行了。最恶心的：\(3\) 次，当且仅当 \(P_1=n,P_n=1\)，必须先换一次把 \(1\) 或者 \(n\) 换出来，然后再进行 \(2\) 次的一般操作。

唯一不太好弄的是 \(1\) 次的情况，那既然 \(1 \sim i-1\) 的数都在它前面，做个前缀和看看是不是等于 \(\sum_{j=1}^{i-1} = \frac{i(i-1)}{2}\) 就行了。

题外话：看到这个 \(1\) 次的处理方法我想到了“由乃与大母神原型和偶像崇拜”，那是个算平方和，于是很自然的打了一棵 SGT。然后交完想起来不带修，就又换成了前缀和……

T3 序序