从位图结构开始学内存的计算

目录

• 位图的定义
• 实践-40亿个QQ号在2G内存去重

---

今天发现从认识位图（Bitmap）结构，可以很好梳理底层的计算机内存结构基础。那就先来认识内存的计算单位：

内存可以比喻成一张巨大的Excel 表格，表格里可以划分不同的Sheet页方便区分不同功能类\区域（类似 堆区，栈区，启动区，命令区，变量区，自由申请区......），开发者设计的程序使用内存的时候，需要进到指定的区，需要设计好在区内使用的边界（大小）这样才能保证程序和系统正常运行，划分边界就需要认识存储单位。

现代的操作系统、高级语言把这些申请步骤都封装好了，程序运行的时候底层自动帮你做了，所以感知不到，知道就行。

存储单位分为：
Bit、Byte、KB、MB、GB、......

除了Bit到Byte是8进率，其它的存储单位间都以 1024 作为进率;

• Bit (位) (b)：计算机存储信息的最小单位（也是计算机最基础的单位），可以存储的值为 0 或 1。

• Byte (字节) (B)：基本存储单位，1 Byte = 8 bits。
  

• KB (千字节) (Kilobyte)：1 KB = 1024 Bytes。

• MB (兆字节) (Megabyte)：1 MB = 1024 KB。

• GB (吉字节) (Gigabyte)：1 GB = 1024 MB。

• .......

32位 和 64位计算机的区别：
我们说的 32 位和 64 位计算机，指的是 CPU 每一次可以处理多少位的数据；

好！基础的内存存储单位复习就到这里。

---

位图的定义

一种数据结构，使用一串二进制位 (0/1) 来表示大量数据的存在状态，以极节省内存来快速判断数据是否在集合中。简而言之，它可以是图像（像素点阵），也可以是记录状态（位序列）的高效数据集合；

核心概念

• 基本单位是位（bit）：位图的核心是利用计算机最小的存储单位——位（bit），每个位只能是0或1。
• 映射关系：一个位代表一个特定的数据项。例如，位图的第N个位（bit）可以表示整数N是否存在于集合中。
• 状态表示：通常用 1 表示“存在”或“真”，0表示“不存在”或“假”。

主要特点

• 极度节省空间：1个位只占1bit (1/8字节)，相比于存储整个数字或字符串，能大幅减少内存占用。
• 高效操作：支持快速的位运算（AND, OR, XOR等），可以实现集合的快速查找、交集、并集、差集等操作。
• 适用场景：海量用户签到状态、黑白名单、数据去重、数据库索引、布隆过滤器等。

与图像位图的区别

• 数据结构位图：一种逻辑概念，关注如何高效存储和操作数据状态。
• 图像位图（点阵图）：一种图像表示方式，每个像素点由一个或多个位表示颜色和亮度，用于显示图像。

位图使用案例：

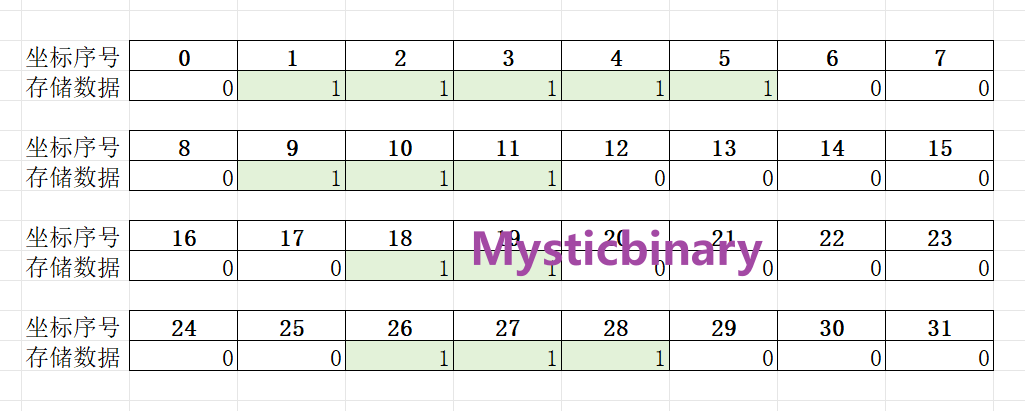
上图只用了 32位=4字节 就表示了一个用户一个月的全部登录记录。
记录方式为：如果登录了系统，那么对应天数的那个bit就设置为1，否则为0。一个月恰好是连续的31天：

---

实践-40亿个QQ号在2G内存去重

问题：一台 2G 内存电脑，要求处理 40 亿个无序10位的QQ号，如何快速去重？

我们先看看存储进内存需要多少内存空间：
一个10位的QQ号：1234567890，需要34位来存储，那么40亿个就是：

34 * 40亿 = 136000000000（Bits）;

136000000000 / (8 * 1024*1024*1024) ≈ 16 (GB);

16G数据是装不进2G内存的。所以想进内存在开始计算的方案都行不通。考虑其他办法吧。

方案二：
以QQ号"9076072220"为例，我们可以按照以下步骤将其放入位图中:

1. 确定位置： 找到对应的位图位置。对于QQ号"9076072220"，我们将其作为索引9076072220；
2. 设置位： 将该位置设置为1，表示该QQ号存在。

通过这种方式，将所有QQ号放入位图后，所有值为1的位置表示存在，不为1的位置表示不存在。对于相同的QQ号，只需设置一次1，因此可以有效地完成去重。

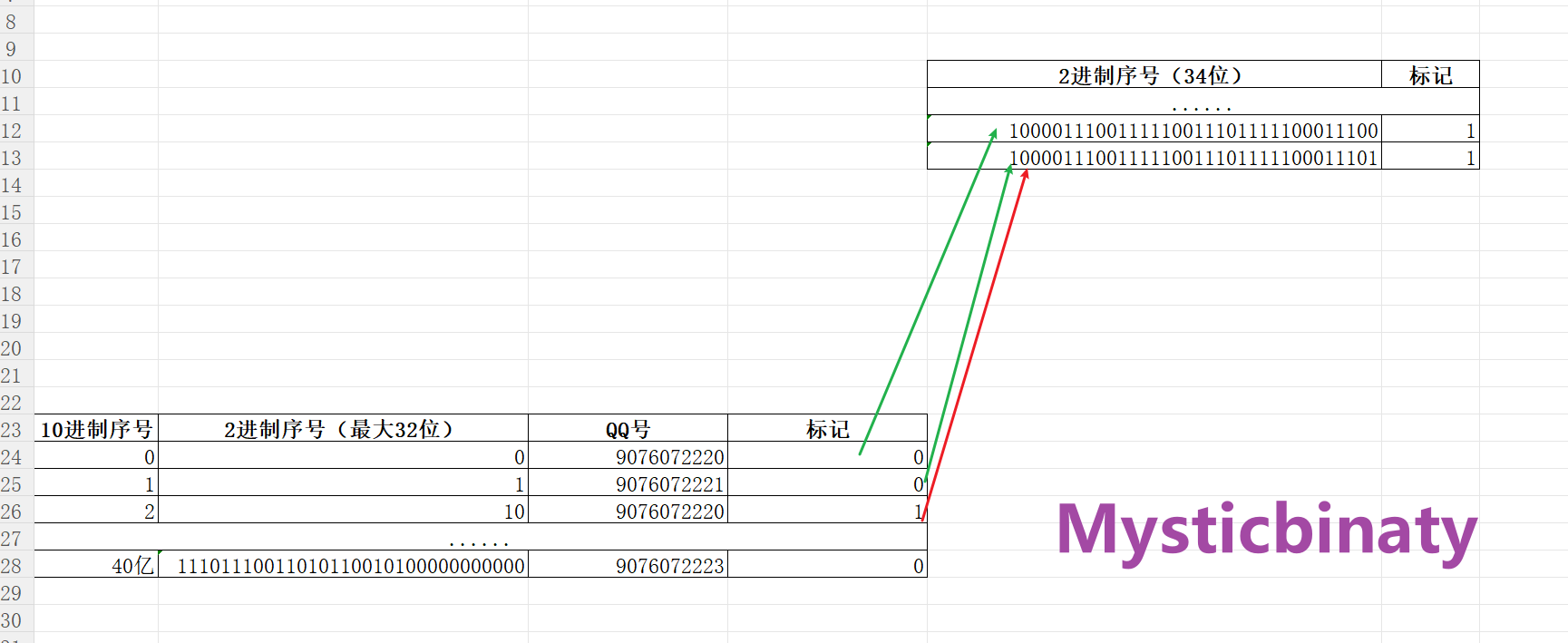
然后计算需要多少内存空间：
10位QQ最大是：9999999999 - 1000000000 = 8999999999 个;
因为：0-999999999 是非10位QQ号，不在本次计算内，所以去掉。
所以：8999999999 * 1bit(标记) = 8999999999 bits;

40亿 * 1 bit(标记) = 40亿 bits ；
40亿 bits + 8999999999 bits = 12999999999 bits;

12999999999 / (8 * 1024 * 1024 * 2024 ) ≈ 0.7 GB

哇！只需要不到1G的空间就可以搞定，相比而言，很省空间了。

时间复杂度：O(n+j)，n 为范围(上图的32位)，j为记录数（上图的34位），都是常数：所以O(1)，非常快。
这个方案简单易懂，高效且低空间。

当然还有其他方案，比如Hash，这里不继续了，Bye.