兄弟们,向量是一种“船新”的框架!系兄弟就砍它一刀。😏
基础概念
向量的定义:
向量(vector,也称矢量),是同时具有数值和方向,且满足平行四边形法则的几何对象。
向量有几种表示方法:
- 几何表示:带箭头的线段;
- 代数表示:黑体小写字母或带箭头的字母 \(\mathbf{a}\) 、 \(\mathbf{u}\) 、$ \vec{a} $ 、 $ \vec{AB} $;
- 坐标系表示法:坐标又分平面和空间:
- 平面坐标系:用数对 (x,y) 表示;
- 空间坐标系:用三元组 (x,y,z)表示;
求向量大小—求模长:

单位化(标准化):
向量单位化(Normalization),也称为标准化,是指将一个非零向量转换为一个单位向量的过程,该单位向量与原向量方向相同,但模长(长度)为1。
和单位圆类似。
加、减、数乘
四边形法则,三角形法则:
平行四边形法则是定义向量加法运算的几何方法。它描述了如何将两个向量合成为一个“合向量”,而这个合成过程在几何图形上恰好构成一个平行四边形。
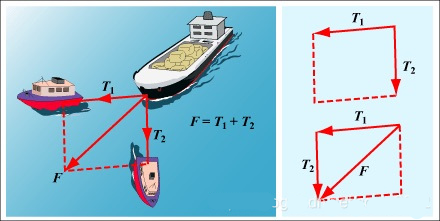
观察:T2的移动过程。
与三角形法则的关系——等价:
平行四边形法则有一个更常用、更简单的等价形式——三角形法则。
三角形法则:
将向量 \(\vec{a}\) 的终点作为向量 \(\vec{b}\) 的起点,那么从 \(\vec{a}\) 的起点指向 \(\vec{b}\) 的终点的向量,就是 \(\vec{a} + \vec{b}\)。
关系:
- 本质上,平行四边形法则中的两条对边是平行且相等的。当你平移向量 \(\vec{b}\) 使其起点与 \(\vec{a}\) 的终点重合时,平行四边形就变成了一个三角形。
- 三角形法则更便于进行多个向量的连续加法(首尾相接)。
总结:
在向量坐标系里,一个向量所在的位置是相对的,可以自由平移。
加减:
规则:将两个向量对应位置的数字(分量)分别相加或相减。
几何表示法:
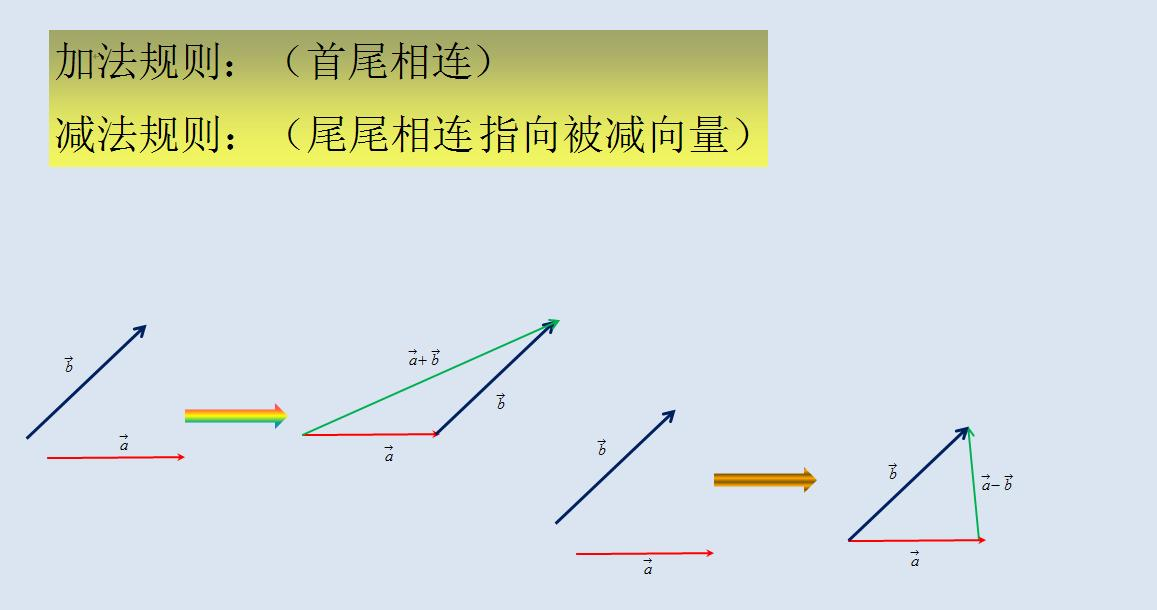
代数计算示例:
若 \(a=(a_{1},a_{2},a_{3})\), \(b=(b_{1},b_{2},b_{3})\)
加法:\(a+b=(a_{1}+b_{1},a_{2}+b_{2},a_{3}+b_{3})\)
减法:\(a-b=(a_{1}-b_{1},a_{2}-b_{2},a_{3}-b_{3})\)
标量乘法(数乘):
非常简单,直接看示例:
若 \(\mathbf{v}=(2,3)\),
标量 \(c=4\),则 \(4\mathbf{v}=(4\times 2,4\times 3)=(8,12)\)
标量 \(c=-1\),则 \(-1\mathbf{v}=(-1\times 2,-1\times 3)=(-2,-3)\)
乘(产生新性质的运算)
点积(内积、数量积)
点积有两种计算方法:
-
代数法
坐标法(对应分量相乘再求和,如 \(A\cdot B=x_{1}x_{2}+y_{1}y_{2}+...\)),结果是一个标量(数字)。 -
几何法
几何法(模长乘积与夹角余弦的乘积,如 $A\cdot B=|A||B|\cos \theta $),结果是一个标量(数字)。

点积的意义:
衡量向量的相似程度,点积为零表示向量正交(垂直)。
-
物理学: 计算力对物体做的功(功 = 力 (\cdot ) 位移),以及力的分解。
-
计算机图形学:判断多边形面朝向摄像机还是背向摄像机。计算光照强度(点积越大,越接近光源方向,光照越强)。实现动画渲染效果。
-
机器学习/人工智能:神经网络中的基础运算,用于特征提取和线性分类器(例如,判断输入向量是否属于某一类)。
-
数据分析/相似度: 反映两个向量的“相似度”,值越大越相似。
疑问:
点积的几何计算法为什么要乘一个余弦值?
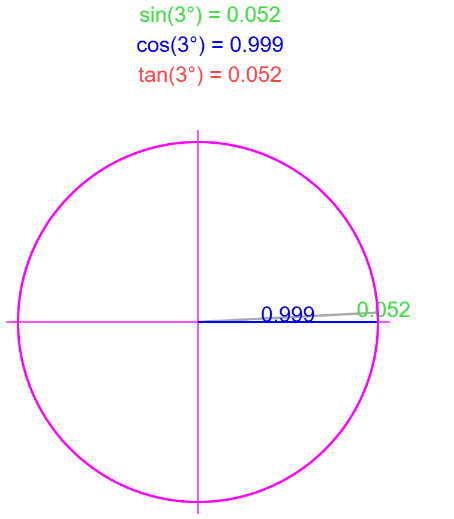
在单位圆中,当斜线和cos线靠得越近,值就会越大,相乘cos大的值,值越大,则说明越相似。
叉积(外积、向量积、矢量积) - 仅适用于三维空间
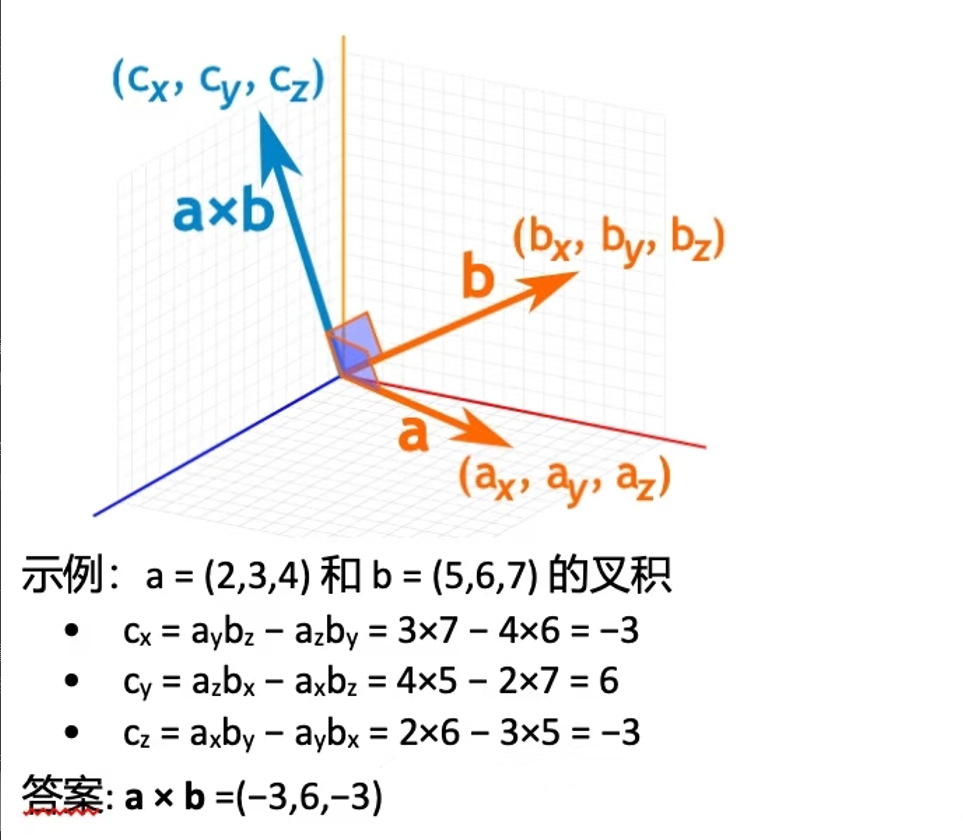

求出的结果向量c垂直于a,b:
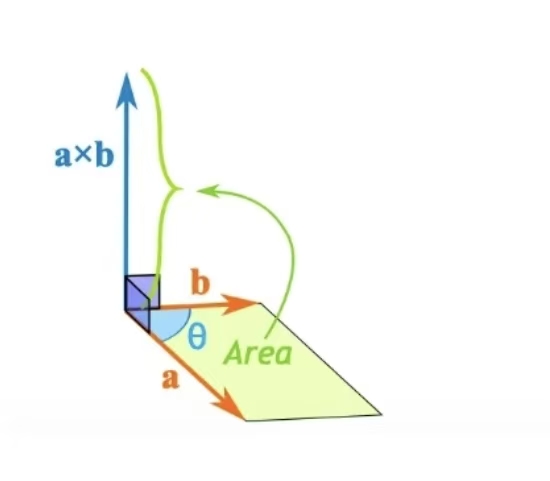

混合积(标量三重积、三重积)
向量混合积,表示为 \(a\cdot (b\times c)\),计算结果是一个标量(一个实数)。它代表由向量 \(a\), \(b\), \(c\) 构成的平行六面体的体积,其绝对值等于体积。

除
提出疑问,为啥向量没有除法呢?

特征值,特征向量

应用:
-
数据降维:主成分分析(PCA)通过找到最大特征值对应的特征向量(主成分)来提取数据最主要的信息。
-
工程/计算机科学: PageRank算法(网页排名)、面部识别(特征脸)、振动分析
向量和复数的关系
复数可以看作是复平面上的向量:
-
复数加减法遵循向量的平行四边形法则;
-
复数乘法则对应于向量长度的缩放和角度的旋转;
-
复数的模长就是向量的长度;
-
两个复数之差的模长代表了复平面上两点间距离。
-
......


 浙公网安备 33010602011771号
浙公网安备 33010602011771号