线性规划（LP）入门

目录

• 原理
• 案例

---

定义：
线性规划是一种在给定约束条件下，寻找最优决策的数学方法。 这里的“最优”通常指的是最大化（如利润）或最小化（如成本、最小路径）某个目标。

“线性”的含义？
指的是模型中所有的数学关系都是线性的，即可以用一次方程（或不等式）来表示。

• 目标函数是线性的：例如，利润 = 5x + 3y。这意味着每生产一个产品x，利润增加5元；每生产一个产品y，利润增加3元。增长是成比例的，不会出现x²或xy这样的项。

• 约束条件也是线性的：例如，2x + 4y ≤ 100。这表示生产x和y所消耗的某种资源（如工时、原材料）是线性累加的，并且总量不能超过100。

“规划”的含义？
线性规划（英语：Linear Programming，简称LP），这里的“规划”并非指制定计划，而是指“优化”或“规划求解”，即从所有可行的方案中，找出最好的那一个。

线性规划属于 运筹学 和 数学优化 这两个紧密相关的数学分支。

---

原理

线性规划基本定理:
它在“可行域”（所有满足约束条件的点构成的区域，是一个凸多边形或多面体）的顶点上进行迭代，从一个顶点移动到相邻的另一个更优的顶点，直到找到最优解。

• 对于标准形式的线性规划问题，如果该问题存在有界的最优解，那么至少有一个最优解在顶点（极点）上。

• 求解线性规划最优解的方法就是穷举所有的顶点，然后找出目标函数最优的那个顶点就是最优解了。

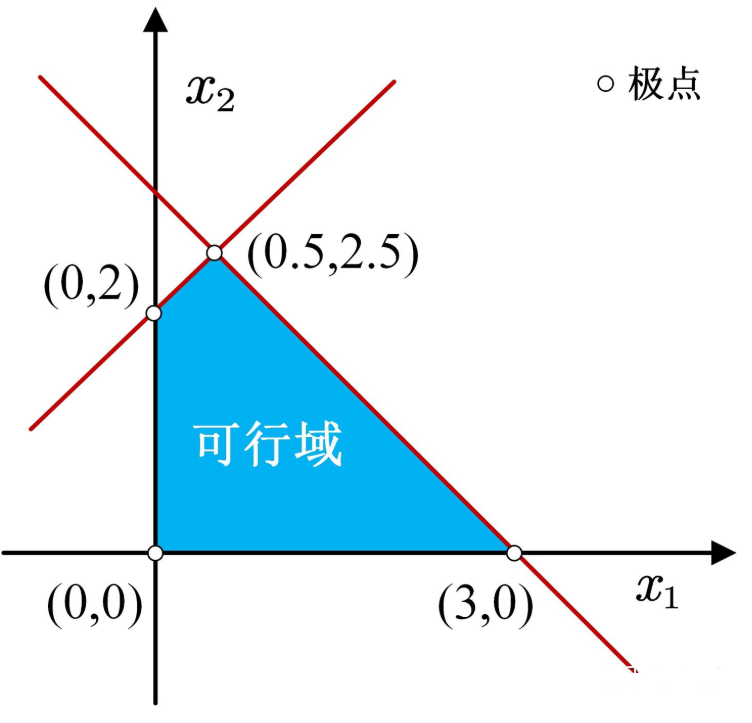
画出该线性规划问题的可行域，并在图中标出所有顶点的坐标。

---

案例

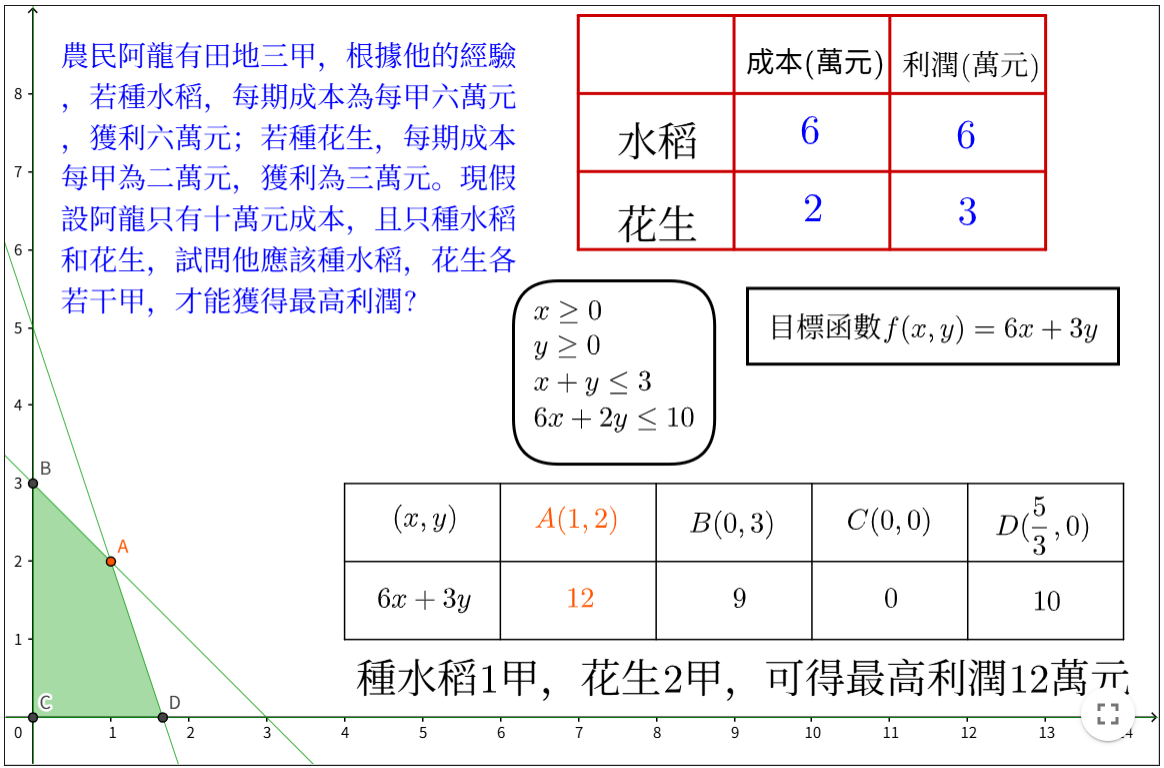
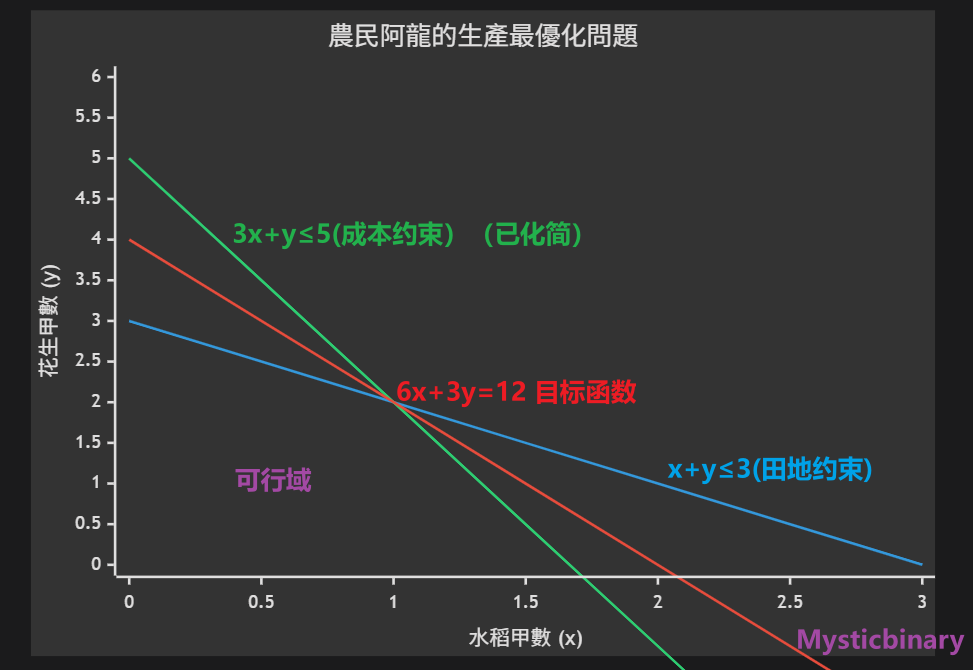
求最大化收益
https://www.geogebra.org/m/xtnyrr2c