樽海鞘优化算法

1. 简介

---

    樽海鞘是一种透明的桶状生物，和水母比较相似。它通过吸水、喷水来移动的。由于它生活在寒带的深海里面，给我们的研究造成了一定的困扰。但是，这并不影响我们对它的研究。在深海里，樽海鞘是以樽海鞘链的形式存在，这就是我们感兴趣的群体行为之一。我们将樽海鞘链分为两个部分：1、领导者；2、追随者。领导者就是樽海鞘链前端的部分；追随者就是樽海鞘链后端的部分。当领导者被设置为樽海鞘链的前半部分时，算法效率更高。

2. 算法核心

---

领导者的位置更新公式：

\[x_j^1= \left\{ \begin{matrix} F_j + c_1((ub_j - lb_j)c_2 + lb_j) & c_3\geq0\\ F_j - c_1((ub_j - lb_j)c_2 + lb_j) & c_3<0 \end{matrix} \right. \]

其中，\(x_j^1\)是领导者在第\(j\)维的位置; \(F_j\)表示食物在第\(j\)维的位置; \(ub_j\)表示领导者在第\(j\)维的上界， \(lb_j\)表示领导者在第\(j\)维的下界; \(c_1\), \(c_2\), \(c_3\)。\(c_1=2e^{-(\frac{4l}{L})}\), 其中，\(l\)表示当前迭代次数，\(L\)表示最大迭代次数。
追随者位置更新公式：

\[x_j^i=\frac{1}{2}(x_j^i + x_j^{i-1}) \]

3. matlab代码实现(两个版本)

---

第一版

clc
clear
close all;

npop = 50;        % 种群规模
nVar = 3;         % 变量维数
max_iter = 1000;     % 最大迭代次数

lb = -100;  % 下界
ub =  100;  % 上界

obj = @ sphere;   % 目标函数

%% 初始化
SalpPositions = zeros(npop,nVar);
SalpFitness = zeros(1,npop);

FoodPosition = zeros(1,nVar);  % 食物位置
FoodFitness = inf; 

% 初始化种群并计算个体适应度
for i=1:npop
    SalpPositions(i,:) = lb + rand(1,nVar)*(ub-lb);  
    SalpFitness(i) = obj(SalpPositions(i,:));
    
    if SalpFitness(i)<FoodFitness
       FoodPosition = SalpPositions(i,:);
       FoodFitness = SalpFitness(i);
    end
end
best_scores = [FoodFitness];
%% SSA算法开始
for iter=1:max_iter
    c1 = 2*exp(-(4*iter/max_iter)^2);  % 设置参数
    for i=1:npop
        if i<=npop/2
            for j=1:nVar
                c2 = rand();
                c3 = rand();
                if c3<0.5
                    SalpPositions(i,:) = FoodPosition + c1*((ub - lb)*c2 + lb);
                else
                    SalpPositions(i,:) = FoodPosition - c1*((ub - lb)*c2 + lb);
                end
            end
        elseif i > npop/2 && i < npop+1
            point1 = SalpPositions(i-1,:);
            point2 = SalpPositions(i,:);
            SalpPositions(i,:) = (point1 + point2)/2;
        end
       %% 边界修正
        Tp = SalpPositions(i,:)>ub;
        Tm = SalpPositions(i,:)<lb;
        SalpPositions(i,:) = SalpPositions(i,:).*(~(Tp+Tm)) + ub.*Tp + lb.*Tm;
        
       %% 进化机制
        SalpFitness(i) = obj(SalpPositions(i,:));
        
       if SalpFitness(i)<FoodFitness
            FoodPosition = SalpPositions(i,:);
            FoodFitness = SalpFitness(i);
        end
    end
    disp(['Iter=', num2str(iter), '   ||  fmin=', num2str(FoodFitness)]);
    best_scores = [best_scores,FoodFitness];
end

%% SSA可视化
figure
xx = 1:50:1001;
xxx = 0:50:1000;
plot(xxx,log10(best_scores(xx)),'r','LineWidth',1.5);
hold on;
sz = 40;
scatter(xxx(2:end-1),log10(best_scores(xx(2:end-1))),sz,'ro','filled');
xlabel('$$Iteration$$','Interpreter','latex');
ylabel('$$\log_{10} (fitness)$$','Interpreter','latex');
title('Convergence curve')

第二版

clc
clear
close all;
 
%%  问题定义
CostFunction = @(x) sphere(x);  %  目标函数

nVar = 2;                       %  变量的维数
VarSize = [1,nVar];             %  变量的矩阵大小

VarMin =-100;                   %  变量的下确界
VarMax = 100;                   %  变量的上确界

%%  SSA参数
MaxIt = 1000;            % 最大迭代次数
nPop = 50;               % 种群大小

%%  初始化
empty_slaps.Position = [];  % 樽海鞘模板
empty_slaps.Cost = [];

% 创建种群数组
slaps = repmat(empty_slaps,nPop,1);

% 初始化食物的适应度
Food.Cost = inf;

% 初始化种群
for i=1:nPop
    slaps(i).Position = VarMin + (VarMax-VarMin)*rand(VarSize);  % 初始化种群
    slaps(i).Cost = CostFunction(slaps(i).Position);  % 评价
    
    % 更新食物的位置
    if slaps(i).Cost < Food.Cost
       Food = slaps(i);
    end
        
end

BestCosts = zeros(MaxIt,1);

%%  SSA算法的主程序
for it=1:MaxIt
    c1 = 2*exp(-(4*it/MaxIt)^2);  % 设置参数
    for i=1:nPop
        if i <= nPop/2
            c2=rand();
            c3=rand();
            
            if c3<0.5 
                slaps(i).Position =Food.Position + c1*((VarMax - VarMin)*c2 + VarMin);  % 公式3.1
            else
                slaps(i).Position =Food.Position - c1*((VarMax - VarMin)*c2 + VarMin);
            end
        elseif i > nPop/2 && i < nPop+1
            point1 = slaps(i-1).Position;
            point2 = slaps(i).Position;
            slaps(i).Position = (point2 + point1)/2;  % 公式3.4
        end
        
        % 边界处理
        Tp = slaps(i).Position>VarMax;
        Tm = slaps(i).Position<VarMin;
        slaps(i).Position = slaps(i).Position.*(~(Tp+Tm)) + VarMax.*Tp + VarMin.*Tm;
        
        %  计算适应度值
        slaps(i).Cost = CostFunction(slaps(i).Position);  
        
        % 保留精英
        if slaps(i).Cost < Food.Cost 
            Food = slaps(i);
        end 
    end
    
    BestCosts(it) = Food.Cost;
    disp(['Iteration ' num2str(it) ': Best Cost = ' num2str(BestCosts(it))]);
end

目标函数文件

%%  目标函数
function  z  = sphere(x)
%UNTITLED2 Summary of this function goes here
%   Detailed explanation goes here
    z = sum(x.^2);
end

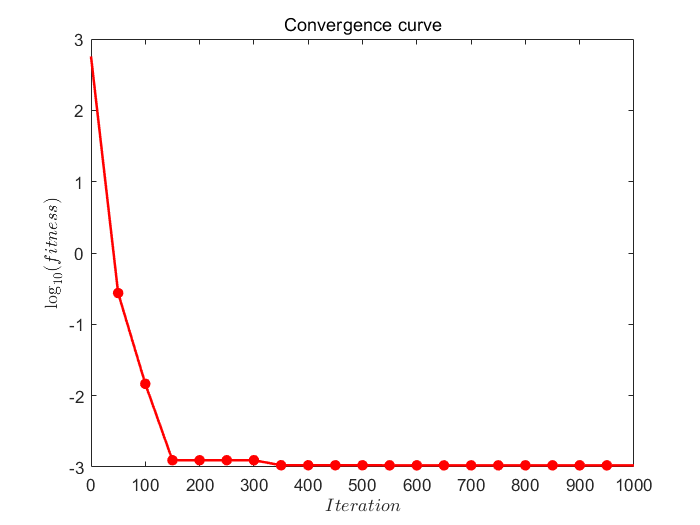
4. 可视化结果