#0019. 神奇的括号序列

题目大意：

　　给定一个长度为n的括号序列。每步可以选择三种操作中的一个：1.向左移动一个 2.向右移动一个 3.移动到当前半括号的另外一半去。

　　m次询问，从u到v的最少步数

　　n,m<=1e5

题目解法：

　　Part 1 转化

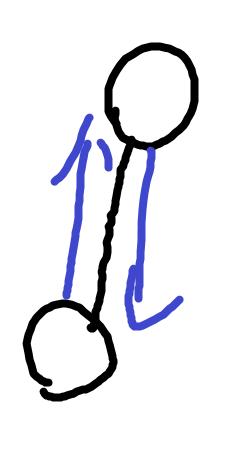
　　这道题最重要的一个套路就是把括号序列转化成一棵树的dfs序。每一个括号序列都对应着一个唯一地树的dfs序。左括号往下加新点右括号往父亲节点跳。

　　我们把括号序列变成一个树后问题就变成了从树上的一条有向边转移到另一条有向边的最少步数。

　　我们把u到fa_u的那条有向边编号为(u,1)，fa_u到u的那条有向边编号为(u,0)

　　考虑操作对应的树上操作。

　　1.移动到对应括号的另一半->对于任意一条边u->v的边，都可以与v->u的边互相转移

 

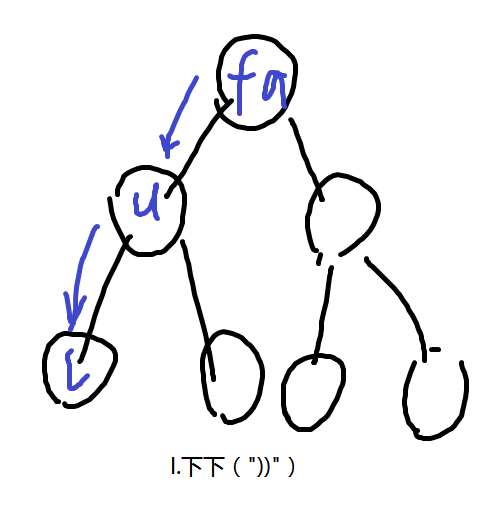
　　2.向相邻位置移动->对于dfs序上相邻的两条边都可以互相转移

 

 

 

  

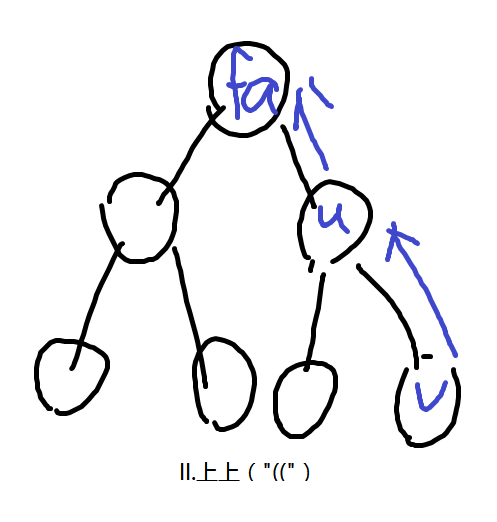
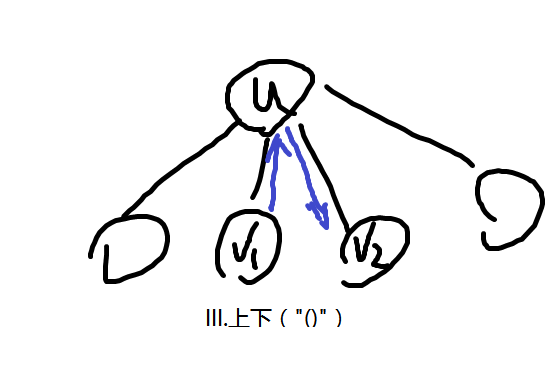
IV.下上（")("），与1种情况重合

其中I需满足v是u的第一个儿子，II需要满足v是u的最后一个儿子，III需要满足v1,v2是两个相邻的儿子。

Part 2 倍增数组的建立

可以注意到I II是跨层转移 III是同层转移

所以对于任意一条边，如果要转移到另一个深度较小的同一条链上的边一定是不断向上跳父亲节点。而如果一个点的一条边想到达其父亲节点的边，必然是先进行同层转移换到第一条边或者最后一条边，然后跨层转移。而对于同层间(x1,y1)到(x2,y2)的转移，代价是|x1+y1-(x2+y2)|，因此到父亲节点是可以O(1)求出的。然后就可以用倍增优化跳父亲的过程。我们可以在O(n log n)的时间复杂度内处理出f[i][j][x][y]数组，表示边(i,x)跳到深度小2^j层的祖先(fa[i][j],y)所需要的步数。

Part 3 利用lca拆分路径并分类讨论

还可以注意到所有转移都是双向的，也就是说如果边a能转移到边b则边b一定能转移到边a。所有u->v和v->u是完全等价的

所以我们从u->v的是以下两种算法取min的结果：

（令w=lca(u,v)）

1.u和v都跳到w的下一层，然后通过同层转移相遇

2.u和v都跳到(w,1)或(w,0)

Done