Bellma-Ford

Bellma-Ford 单源最短路算法

 思路还是找中转点

 

for (int i = 1; i <= m; i++)

将每个点作为中转点尝试一下

 

if (dis[e[i].v] > dis[e[i].u] + e[i].w)

如果从1到e[i].v的路程比先从1到e[i].u再到e[i].v要长，那么就更新dis数组

dis[e[i].v] = dis[e[i].u] + e[i].w;

 

因为dis[0]不用松弛，所以算法进行m-1轮

for(int t = 1; t <= m-1; t++)

 

核心语句

void bf() {    
    for (int t = 1; t <= m - 1; t++)
        for (int i = 1; i <= m; i++)
            if (dis[e[i].v] > dis[e[i].u] + e[i].w)
                dis[e[i].v] = dis[e[i].u] + e[i].w;
    return;
}        

 

初始化

因为是找最短路，所以不相连的点我们将边赋一个INF，以便以后不会取到这条边

1到1距离本来就是0，所以我们从2开始初始化，dia[1]就让它一直是0就好了

    for (int i = 2; i <= n; i++)
        dis[i] = INF;

 

然后这里的邻接表有点特殊

if (dis[e[i].v] > dis[e[i].u] + e[i].w)

 

因为要找以连向dis[e[i].v]的某个点，所以我们要在结构体里加一个元素储存这条边的起点

struct edge {
    int next, v, w, u;
}e[N];

这里的u就是这条边的起点，所以我们用e[i].u来访问第i条边的起点

 

然后在建图的时候直接把起点存就好了

e[total].u = u;

这里的u是输入的起点

 

完整代码：

#include <iostream>
#include <cstdio>
#define N 23333
#define INF 23333333

int head[N], total, m, n, dis[N];

struct edge {
    int next, v, w, u;
}e[N];

void add(int u, int v,int w) {
    total++;
    e[total].u = u;
    e[total].w = w;
    e[total].v = v;
    e[total].next = head[u];
    head[u] = total;
    return;
}

void bf() {
    for (int t = 1; t <= m - 1; t++)
        for (int i = 1; i <= m; i++)
            if (dis[e[i].v] > dis[e[i].u] + e[i].w)
                dis[e[i].v] = dis[e[i].u] + e[i].w;
    return;
}

int main() {
    scanf("%d %d", &n, &m);
    for (int i = 2; i <= n; i++)
        dis[i] = INF;

    for (int i = 1; i <= m; i++) {
        int a, b, c;
        scanf("%d%d%d", &a, &b,&c);
        add(a, b,c);
    }
    
    bf();

    for (int i = 1; i <= n; i++)
        printf("%3d", dis[i]);
    return 0;
}

 

测试数据

6 9
1 2 1
1 3 12
2 3 9
2 4 3
3 5 5
4 3 4
4 5 13
4 6 15
5 6 4

 

硬核画图

 

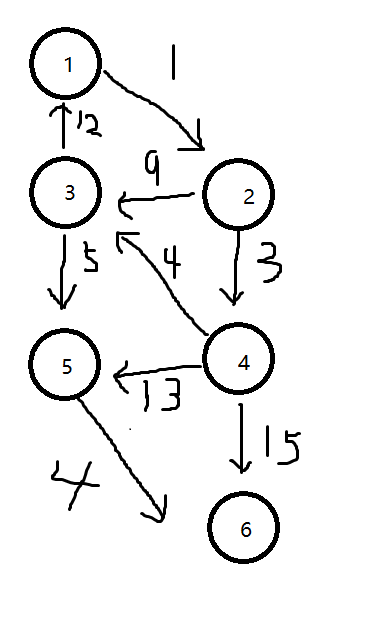
结果

0  1  8  4 13 17