5.3误差逆传播算法推导

\(E_k = \frac{1}{2}\sum_j(\hat{y}_j-y_j)^2\)

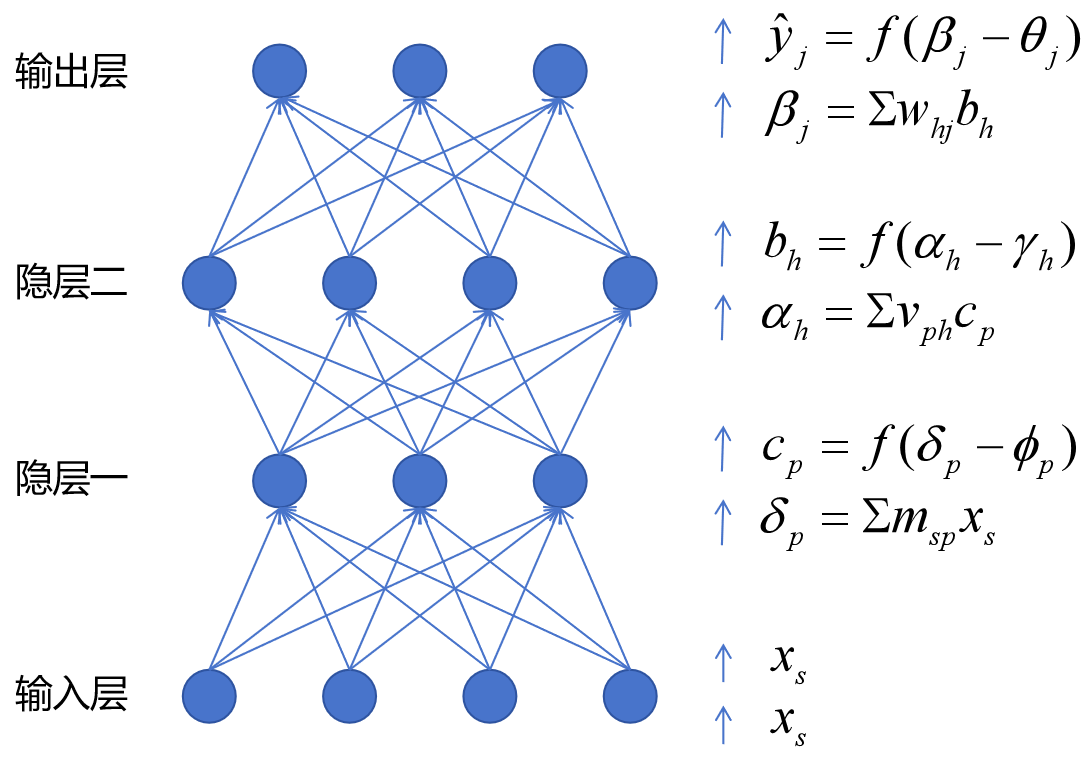
首先找到每层参数到误差的传递关系, 然后\(-\eta\cdot导数\)得到变化量
导数用链式法则, 神经元的激活函数sigmoid函数用对率函数\(f(x) = \frac{1}{1+e^{-x}}\)时, 其导数为\(\frac{\partial f}{\partial x}=f(1-f)\)
而且要注意相同指标求和, 对应于一个神经元的输入影响这个神经元对下一层所有神经元的输入

1. 倒数第一层

\[w_{hj}\rightarrow \beta_j\rightarrow\hat{y}_j\rightarrow E_k \]

\[\theta_j\rightarrow \hat{y}_j\rightarrow E_k \]

\(\Delta w_{hj}=-\eta\frac{\partial E_k}{\partial w_{hj}} = -\eta\frac{\partial E_k}{\partial\hat{y}_j}\frac{\partial\hat{y}_j}{\partial \beta_j}\frac{\partial \beta_j}{\partial w_{hj}} = -\eta[\hat{y}_j-y_j][\hat{y}_j(1-\hat{y}_j)][b_h]=\eta g_jb_h\)

\(\Delta \theta_j=-\eta\frac{\partial E_k}{\partial \theta_{j}} = -\eta\frac{\partial E_k}{\partial\hat{y}_j}\frac{\partial\hat{y}_j}{\partial \theta_j} = -\eta[\hat{y}_j-y_j][\hat{y}_j(1-\hat{y}_j)][-1]=-\eta g_j\)
其中 \(g_j = -\frac{\partial E_k}{\partial\hat{y}_j}\frac{\partial\hat{y}_j}{\partial \beta_j}=-[\hat{y}_j-y_j][\hat{y}_j(1-\hat{y}_j)]\)

2. 倒数第二层

\[v_{ph}\rightarrow\alpha_h\rightarrow b_h\rightarrow \beta_j\rightarrow\hat{y}_j\rightarrow E_k \]

\[\gamma_h\rightarrow b_h\rightarrow \beta_j\rightarrow\hat{y}_j\rightarrow E_k \]

\( \Delta v_{ph}=-\eta\frac{\partial E_k}{\partial v_{ph}} = -\eta\frac{\partial E_k}{\partial\hat{y}_j}\frac{\partial\hat{y}_j}{\partial \beta_j}\frac{\partial \beta_j}{\partial b_{h}}\frac{\partial b_h}{\partial \alpha_h}\frac{\partial\alpha_h}{\partial v_{ph}} = -\eta[\hat{y}_j-y_j][\hat{y}_j(1-\hat{y}_j)][w_{hj}][b_h(1-b_h)][C_p] =\eta\underline{g_jw_{hj}}b_h(1-b_h)C_p = \eta C_pb_h(1-b_h)\sum_jg_jw_{hj}=\eta e_hC_p \)
\(\Delta \gamma_h=-\eta\frac{\partial E_k}{\partial \gamma_{h}} = -\eta\frac{\partial E_k}{\partial\hat{y}_j}\frac{\partial\hat{y}_j}{\partial \beta_j}\frac{\partial \beta_j}{\partial b_{h}}\frac{\partial b_h}{\partial \gamma_h}=-\eta[\hat{y}_j-y_j][\hat{y}_j(1-\hat{y}_j)][w_{hj}][b_h(1-b_h)][-1]=-\eta e_h\)
其中 \(e_h = -\frac{\partial E_k}{\partial\hat{y}_j}\frac{\partial\hat{y}_j}{\partial \beta_j}\frac{\partial \beta_j}{\partial b_h}\frac{\partial b_h}{\partial \alpha_h}=-[\hat{y}_j-y_j][\hat{y}_j(1-\hat{y}_j)][w_{hj}][b_h(1-b_h)]=\underline{g_jw_{hj}}b_h(1-b_h)=b_h(1-b_h)\sum_j{g_jw_{hj}}\)

3. 倒数第三层

\[m_{sp}\rightarrow S_p\rightarrow C_p\rightarrow\alpha_h\rightarrow b_h\rightarrow \beta_j\rightarrow\hat{y}_j\rightarrow E_k \]

\[\phi_p\rightarrow C_p\rightarrow\alpha_h\rightarrow b_h\rightarrow \beta_j\rightarrow\hat{y}_j\rightarrow E_k \]

\( \Delta m_{sp}=-\eta\frac{\partial E_k}{\partial m_{sp}} = -\eta\frac{\partial E_k}{\partial\hat{y}_j}\frac{\partial\hat{y}_j}{\partial \beta_j}\frac{\partial \beta_j}{\partial b_{h}}\frac{\partial b_h}{\partial \alpha_h}\frac{\partial\alpha_h}{\partial C_{p}}\frac{\partial C_p}{\partial S_p}\frac{\partial S_p}{\partial m_{sp}} = -\eta[\hat{y}_j-y_j][\hat{y}_j(1-\hat{y}_j)][w_{hj}][b_h(1-b_h)][v_{ph}][C_p(1-C_p)][x_p] =\eta\underline{\underline{g_jw_{hj}}b_h(1-b_h)[v_{ph}]}[C_p(1-C_p)][x_p]=\eta\underline{e_hv_{ph}}C_p(1-C_p)x_p= \eta [C_p(1-C_p)\sum_he_hv_{ph}]x_p=\eta n_px_p \)
\(\Delta \gamma_h=-\eta\frac{\partial E_k}{\partial \gamma_{h}} = -\eta\frac{\partial E_k}{\partial\hat{y}_j}\frac{\partial\hat{y}_j}{\partial \beta_j}\frac{\partial \beta_j}{\partial b_{h}}\frac{\partial b_h}{\partial \alpha_h}\frac{\partial\alpha_h}{\partial C_{p}}\frac{\partial C_p}{\partial S_p}=-\eta[\hat{y}_j-y_j][\hat{y}_j(1-\hat{y}_j)][w_{hj}][b_n(1-b_n)][v_{ph}][C_p(1-C_p)][-1]=-\eta n_p\)
其中 \(n_p = -\frac{\partial E_k}{\partial\hat{y}_j}\frac{\partial\hat{y}_j}{\partial \beta_j}\frac{\partial \beta_j}{\partial b_{h}}\frac{\partial b_h}{\partial \alpha_h}\frac{\partial\alpha_h}{\partial C_{p}}\frac{\partial C_p}{\partial S_p}=-[\hat{y}_j-y_j][\hat{y}_j(1-\hat{y}_j)][w_{hj}][b_h(1-b_h)][v_{ph}][C_p(1-C_p)]=\underline{\underline{g_jw_{hj}}b_h(1-b_h)[v_{ph}]}[C_p(1-C_p)]=C_p(1-C_p)\underline{e_hv_{ph}}=C_p(1-C_p)\sum_j{e_hv_{ph}}\)![神经网络示意图]