0-1背包问题

一、实验目的

1.掌握动态规划算法解决问题的一般步骤。

2.掌握动态规划法，回溯法的原理，并能过按其原理实现解决0-1背包问题，加深了对0-1背包问题的理解。

二、问题描述

给定n种物品和一背包。物品i的重量是wi，其价值为vi，背包的容量为C。问应如何选择装入背包的物品，使得装入背包中物品的总价值最大？

三、实验代码

#include <iostream>
#include <algorithm>
using namespace std;
struct item{
    int weight;//物品的重量
    int value;//物品的价值
    float va;//物品单位重量的价值
    float rate;//使用率：1代表物品完整放入，小于1代表按比例放入 
}items[100];
bool cmp(const item &a,const item &b){
    return a.va>b.va;
}
int main(){
    int n;//n件物品
    float c;//背包容量为c
    cout<<"请输入物品的数量和背包的容量："<<endl;
    cin>>n>>c;
    cout<<"依次输入每件物品的价值和重量："<<endl;
    //v[n]：n件物品的价值，w[n]：n件商品的重量
    float *v = new float[n];
    float *w = new float[n];
    for(int i=0;i<n;i++){
        cin>>items[i].value>>items[i].weight;
        items[i].va=items[i].value/items[i].weight;//计算单位重量价值
        items[i].rate=0;//初始化每件物品的使用率
    }
    sort(items,items+n,cmp);//按照单位重量的价值排序
    int sum=0,j=0;
    for(j=0;j<n;j++){
        if(items[j].weight<=c){//选择单位价值重量最大的并且不超过背包容量的
            items[j].rate=1;
            sum+=items[j].weight;
            c-=items[j].weight;
            cout<<"放入背包的物品："<<"重量为："<<items[j].weight<<"\n价值为："<<items[j].value<<endl<<"放入比例："<<items[j].rate<<endl;
        }
        else break;
    }
    if(j<n){//物品未装完
        items[j].rate=c/items[j].weight;//背包容量还剩c,计算出未装入的物品能装多少的比例
        sum+=items[j].rate*items[j].weight;//加上装入部分比例物品的重量
        cout<<"重："<<items[j].weight<<"、价值："<<items[j].value<<"被放入了背包"<<endl<<"放入比例："<<items[j].rate<<endl;
    }
    delete[] v , w;
    return 0;
}

四、实验结果

当物品的重量小于背包容量时，输出物品的重量和价值，输出比例为1

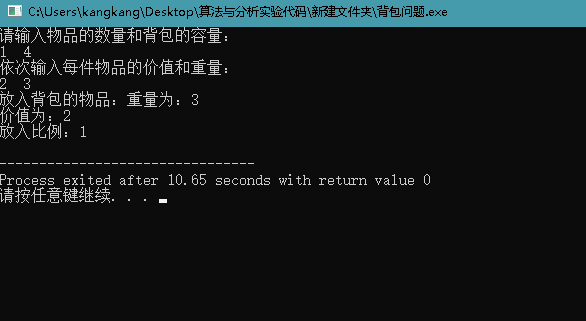
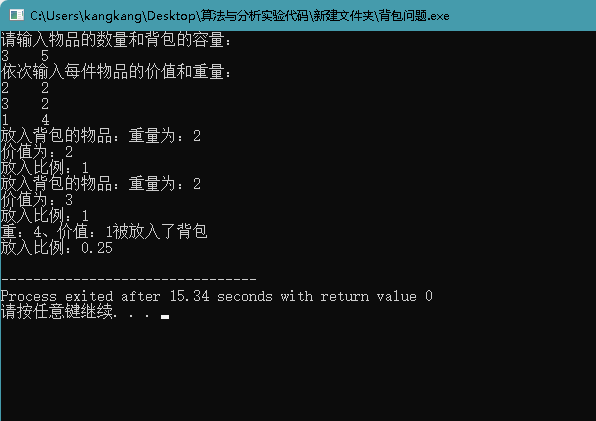
随着放入物品数量的增加，当重量大于背包容量时，放入比例就等于（背包容量-该物品之前的重量之和）/该物品的重量