排列组合算法模板https://img-blog.csdnimg.cn/20210403001620397.png?x-oss-process=image/watermark,type_ZmFuZ3p
一,排列
1.无重复元素
(1).打印n个数的全排列
LC46
List<List<Integer>> ans = new ArrayList<>();
List<Integer> tans = new ArrayList<>();
public List<List<Integer>> permute(int[] nums) {
int [] book = new int[nums.length];
Arrays.sort(nums);
backTrack(book,nums);
System.out.println(tans);
return ans;
}
public void backTrack(int [] book,int [] nums){
if (tans.size()==nums.length){
ans.add(new ArrayList<>(tans));
System.out.println(tans);
}
for (int i = 0; i < nums.length; i++) {
if (book[i]==0){
book[i]=1;
tans.add(nums[i]);
backTrack(book,nums);
book[i]=0;
tans.remove(tans.size()-1);
}else continue;
}
}
(2).打印n个数中任意m个数的全排列
List<List<Integer>> ans = new ArrayList<>();
List<Integer> tans = new ArrayList<>();
public void backTrack(int [] book,int [] nums,int m){
if (tans.size()==m){
ans.add(new ArrayList<>(tans));
System.out.println(tans);
}
for (int i = 0; i < nums.length; i++) {
if (book[i]==0){
//nums[i]<tans.get(tans.size()-1)保证结果是有序的,就可以避免重复计算
if (tans.size()>0&&nums[i]<tans.get(tans.size()-1)) continue;
//和3基本上一样
book[i]=1;
tans.add(nums[i]);
backTrack(book,nums,m);
book[i]=0;
tans.remove(tans.size()-1);
}else continue;
}
}
2.有重复元素
(1)给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。
LC47:
题解:https://leetcode-cn.com/problems/permutations-ii/solution/47hui-su-jian-zhi-zhong-fu-shu-by-bu-zhi-h7dm/
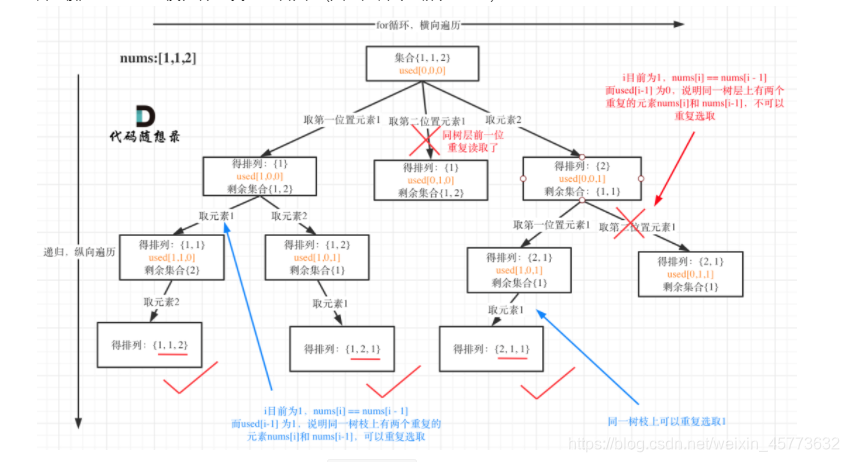
主要讲一下为什么剪枝条件加了一个!used[i-1]?其实图里也很清楚,我们知道重复必定发生在决策树的同一层,当我们只有i>0 && nums[i] == nums[i-1]时,有一种可能是nums[i-1]和nums[i]在同一条路径上,nums[i-1]是num[i]的父节点,对应图中左下的箭头,是生成[1,1*]的那条路,可以重复选。而我们需要剪的是回溯到选第一个位置时,选到第二个1,这个和之前的那个1是同一层的,而且是重复的,因此必须再加上一个!used[i-1]来保证不是重复选择[1,1*]的情况确实是同一层选重复了。
比如[1,1,2],第一次选了第一个1,第二次是可以选第二个1的,虽然它和前一个1相同。
因为前一个1被选过了,它在本轮已经被第一条规则修掉了,所以第二轮中第二个1是可选的。
输入:nums = [1,1,2]
输出:
[[1,1,2],
[1,2,1],
[2,1,1]]
写法1:
boolean[] vis;
public List<List<Integer>> permuteUnique(int[] nums) {
List<List<Integer>> ans = new ArrayList<List<Integer>>();
List<Integer> perm = new ArrayList<Integer>();
vis = new boolean[nums.length];
Arrays.sort(nums);//很重要
backtrack(nums, ans, 0, perm);
return ans;
}
/**
* @param idx 选择到第几个数
*
* 难点在于保证在同一个位置,一个数字只能被选择一次
*/
public void backtrack(int[] nums, List<List<Integer>> ans, int idx, List<Integer> perm) {
if (idx == nums.length) {
ans.add(new ArrayList<Integer>(perm));
return;
}
for (int i = 0; i < nums.length; ++i) {
if (vis[i] || (i > 0 && nums[i] == nums[i - 1] && !vis[i - 1])) {
continue;
}
perm.add(nums[i]);
vis[i] = true;
backtrack(nums, ans, idx + 1, perm);
vis[i] = false;
perm.remove(idx);
}
}
写法2:
public static void main(String[] args) {
LC47 a = new LC47();
int [] nums = {1,1,2};
System.out.print(a.permuteUnique(nums));
}
List<List<Integer>> ans = new ArrayList<>();
List<Integer> tans = new ArrayList<>();
public List<List<Integer>> permuteUnique(int[] nums) {
int [] book = new int[nums.length];
Arrays.sort(book);
backTrack(nums,book);
return ans;
}
public void backTrack(int nums [],int book []){
if (tans.size()==nums.length){
ans.add(new ArrayList<>(tans));
}
//根据题意:画树状图可以知道,重复的排列是在同一层中产生的
//这里的t用于子同一层中标记相同的数是否重复出现,t的初始值只要不是nums[]中的数都可以
int t=11;
for (int i = 0; i < nums.length; i++) {
if (book[i]==0&&nums[i]!=t){
book[i]=1;
t=nums[i];
tans.add(nums[i]);
backTrack(nums,book);
book[i]=0;
tans.remove(tans.size()-1);
}else continue;
}
}
二,组合
1.无重复元素
(1).打印n个数中任意m个数的组合(排列+去重)
LQ_E_20
public static void main(String[] args) {
int [] nums = {1,2,3,4,5,6,7};
permute(nums);
System.out.println(ans);
System.out.println(b);
}
static List<List<Integer>> ans = new ArrayList<>();
static List<Integer> tans = new ArrayList<>();
static int b = 0;
public static List<List<Integer>> permute(int[] nums) {
int [] book = new int[nums.length];
for (int i = 1; i <= 7; i++) {
backTrack(book,nums,i);
}
return ans;
}
/**
* 将数码管的七段进行全排列(用数字代表数码管字段,0代表a,1代表b,以此
* 类推)然后将这7个数字的所有可能全部排列(从7个数字中取m(1<=m<=7)进行排列)列举出来
*
*@param m 表示选几个数字
* @param book 标记在某一轮选取中某一个数是否被选取
* @param nums 存储要被选择的数字
*/
public static void backTrack(int [] book,int [] nums,int m){
if (tans.size()==m){
ans.add(new ArrayList<>(tans));
b++;
}
for (int i = 0; i < nums.length; i++) {
if (book[i]==0){
//nums[i]<tans.get(tans.size()-1)保证结果是有序的,就可以避免重复计算
if (tans.size()>0&&nums[i]<tans.get(tans.size()-1)) continue;
book[i]=1;
tans.add(nums[i]);
backTrack(book,nums,m);
book[i]=0;
tans.remove(tans.size()-1);
}else continue;
}
}
LC77 组合(给定两个整数 n 和 k,返回 1 … n 中所有可能的 k 个数的组合。)
解法1(最大搜索起点)
List<List<Integer>> ans = new ArrayList<>();
Deque<Integer> tans = new ArrayDeque<>();
public List<List<Integer>> combine(int n, int k) {
dfs(n, k, 1);
return ans;
}
private void dfs(int n, int k, int begin) {
if (tans.size() == k) {
ans.add(new ArrayList<>(tans));
return;
}
//这里n - (k - tans.size()) + 1是一个剪枝优化,实际上写成 i<= n也可以
for (int i = begin; i <= n - (k - tans.size()) + 1; i++) {
tans.addLast(i);
dfs(n, k, i + 1);
tans.removeLast();
}
}
解法2(对每个数考虑选还是不选)
List<List<Integer>> res = new ArrayList<>();
Deque<Integer> path = new ArrayDeque<>();
public List<List<Integer>> combine(int n, int k) {
// 为了防止底层动态数组扩容,初始化的时候传入最大长度
dfs(1, n, k);
return res;
}
private void dfs(int begin, int n, int k) {
if (k == 0) {
res.add(new ArrayList<>(path));
return;
}
// 基础版本的递归终止条件:if (begin == n + 1) {
if (begin > n - k + 1) { //n-k+1是搜索起点上界
return;
}
// 不选当前考虑的数 begin,直接递归到下一层
dfs(begin + 1, n, k);
// 不选当前考虑的数 begin,递归到下一层的时候 k - 1,这里 k 表示还需要选多少个数
path.addLast(begin);
dfs(begin + 1, n, k - 1);
// 深度优先遍历有回头的过程,因此需要撤销选择
path.removeLast();
}
(2) 从一组数种选择m个数使得这m个数的和等于目标值(可重复选择某一个数)
LC39
题解链接:https://leetcode-cn.com/problems/combination-sum/solution/hui-su-suan-fa-jian-zhi-python-dai-ma-java-dai-m-2/
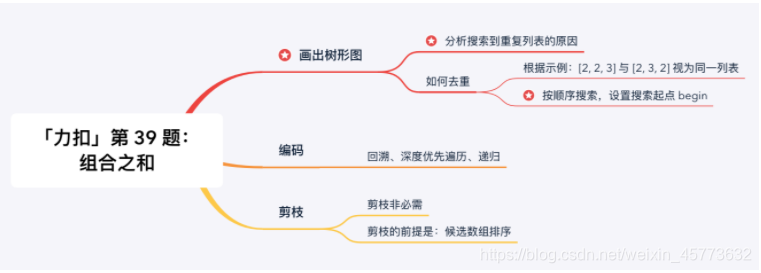
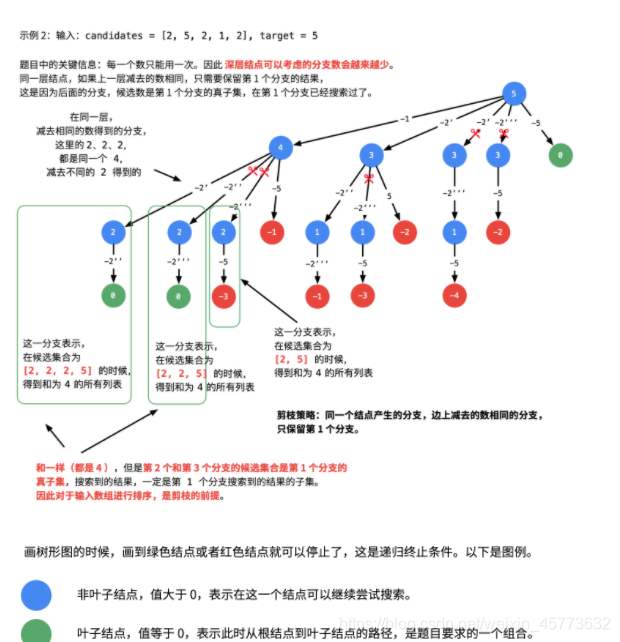
产生重复的原因:在每一个结点,做减法,展开分支的时候,由于题目中说 每一个元素可以重复使用,我们考虑了 所有的 候选数,因此出现了重复的列表。
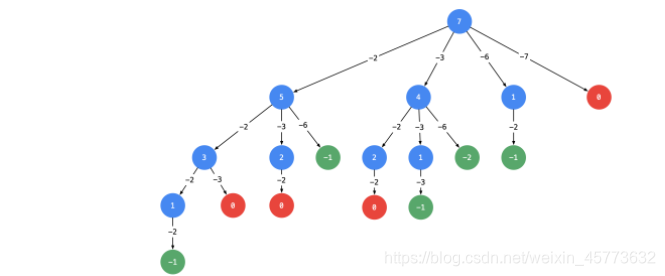
去重:从每一层的第 2 个结点开始,都不能再搜索产生同一层结点已经使用过的 candidate 里的元素。
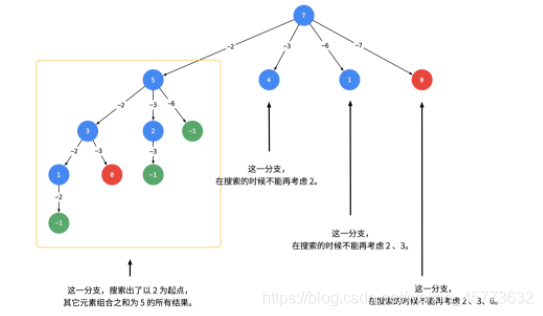
注意:注意for循环的起点
解法1 (做加法)
List<List<Integer>> ans = new ArrayList<>();
List<Integer> tans = new ArrayList();
int t = 0;
public List<List<Integer>> combinationSum(int[] candidates, int target) {
backTrack(0,candidates,target);
return ans;
}
public void backTrack(int begin,int [] candidates,int target){
if (t==target){
System.out.println("加入"+tans);
ans.add(new ArrayList<Integer>(tans));
System.out.println("结果:"+ans);
}else if (t>target) return;
else {
//画出决策树来理解,如何重复选择某一个数字,
//重点理解从begin开始搜索的语义
//从每一层的第 2 个结点开始,都不能再搜索产生同一层结点已经使用过的 candidate 里的元素。
==for (int i = begin; i < candidates.length; i++) {==
tans.add(candidates[i]);
t+=candidates[i];
System.out.println("tans:"+ tans +" "+"t="+t);
==backTrack(i,candidates,target);//重复选择当前的数==
t-=candidates[i];
tans.remove(tans.size()-1);
System.out.println("tans:"+ tans+" "+"t="+t);
}
}
}
写法2:(做减法)
public void backTrack(int cur,int sum,int [] candidates,int target){
if (sum ==target){
ans.add(new ArrayList<Integer>(tans));
System.out.println("加入"+tans);
return;
}
// i==cur很关键
// 主要就分成两部分,一直选取某一个数,和选取下一个数
for (int i = cur; i < candidates.length; i++) {
if (sum +candidates[i]<=target){
System.out.println("sum="+sum);
tans.add(candidates[i]);
System.out.println("i="+i+" "+"tans="+tans);
// 由于一个元素可以被重复使用,所以这里递归式中仍然是i
backTrack(i,sum+candidates[i],candidates,target);
tans.remove(tans.size()-1);
System.out.println("i="+i+" "+"tans="+tans+"sum="+sum);
}
else {
break;
}
}
}
写法3: (对每个数考虑选还是不选)
public void backTrack(int[] candidates, int target, List<List<Integer>> ans, List<Integer> tans, int idx) {
if (idx == candidates.length) {
return;
}
if (target == 0) {
ans.add(new ArrayList<Integer>(tans));
return;
}
//下面这两部分可交换
// 选择当前数
if (target - candidates[idx] >= 0) {
tans.add(candidates[idx]);
System.out.println(tans+" "+"t="+idx);
backTrack(candidates, target - candidates[idx], ans, tans, idx);
tans.remove(tans.size() - 1);
System.out.println(tans+" "+"t="+idx);
}
// 直接跳过
backTrack(candidates, target, ans, tans, idx + 1);
}
(3)LC216 找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数,并且每种组合中不存在重复的数字。(解集不能包含重复的组合。 )
LC216
public static List<List<Integer>> combinationSum3(int k, int n) {
List<List<Integer>> ans = new ArrayList<>();
List<Integer> tans = new ArrayList();
int [] book = new int[10];
backTrack(n,k,0,0,book,ans,tans);
return ans;
}
/**
*(1)book[i]针对的是同一层中的某一个值是否可选,递归返回后必须重置为可选的状态
*(2)tk+1>1可将以某一节点子树全部剪枝,
*(3)tn+i在同一层中,一个点已经满足条件,则同层之中所有其他的点及其子树,都被剪枝
*(4)tk>0&&tans.get(tk-1)>=i当tans中有元素时,就需要保证加入一个元素后一谈有序
*/
public static void backTrack(int n,int k,int tn,int tk,int [] book,List<List<Integer>> ans,List<Integer> tans){
if (tn==n&&tk==k){
ans.add(new ArrayList<>(tans));
}
for (int i = 1; i <= 9; i++) {
if (tk+1>k||tn+i>n) break;//(2)(3)
else if(tk>0&&tans.get(tk-1)>=i)continue;
else if (book[i]==0){
book[i]=1;
tans.add(i);
backTrack(n,k,tn+i,tk+1,book,ans,tans);
book[i]=0;//(1)
tans.remove(tans.size()-1);
}
}
}
2.有重复元素
(1)从n个数中选择m个数且这个m个数之和为目标值(每个数字在每个组合中只能使用一次,结果不能重复)
LC40(重点是解决同一层中不能选择相同的数)
原题解链接:
https://leetcode-cn.com/problems/combination-sum-ii/solution/hui-su-suan-fa-jian-zhi-python-dai-ma-java-dai-m-3/#comment
List<List<Integer>> ans = new ArrayList<>();
List<Integer> tans = new ArrayList();
int t = 0;
public List<List<Integer>> combinationSum2(int[] candidates, int target) {
Arrays.sort(candidates);//排序这一步很重要
backTrack(0,candidates,target);
return ans;
}
public void backTrack(int cur,int [] candidates,int target){
if (t==target){
ans.add(new ArrayList<>(tans));
}
for (int i = cur; i < candidates.length; i++) {
// 小剪枝:同一层相同数值的结点,从第 2 个开始,但由于从该位置起的所有结果已经在该值第一次使用后得到,故
// 再在同样的位置使用同样的值结果一定发生重复,因此跳过,用 continue
if (i>cur && candidates[i]==candidates[i-1]) continue; //同一层当中
if (t+candidates[i]<=target){
t+=candidates[i];
tans.add(candidates[i]);
//元素不可重复利用,故i+1;
backTrack(i+1,candidates,target);
t-=candidates[i];
tans.remove(tans.size()-1);
}else {
break;
}
}
}
3. 蓝桥杯
3.1分组(本质:倒序从n个数中选择m个数)
题目来源:2016年蓝桥杯javaB组省赛第5题
private static int ans;
public static void f(int[] a, int k, int n, String s) {
if (k == a.length) {//尝试过每一种可能
if (n == 0) {//选满了5个人
ans++;
System.out.println("s="+s);
}
return;
}
//一直递归调用,直到到达最后一个小组,结束条件靠n-1和k来限制,
//优先找到最后一个满足条件的结果,然后不断回调,再递归,以得到不同的值
String s2 = s;
for (int i = 0; i <= a[k]; i++) {
f(a, k + 1, n - i, s2); // 填空位置 n-i表示还要选几个人
s2 += (char) (k + 'A'); //这里的K表示选的是第几个小组的人
}
}
public static void main(String[] args) {
int[] a = { 4, 2, 2, 1, 1, 3 };//a中的数字代表各个国家的人数A,B,C...F
f(a, 0, 5, "");
System.out.println(ans);
}
3.2剪邮票(从n个数中选择m个数,并判断连通性)
2016年蓝桥杯javaB组省赛
题目来源:第7题
static int N = 12;
static int M = 5;
static int[] a= new int[]{1,2,3,4,5,6,7,8,9,10,11,12};
static int[] b = new int[M];
public static void main(String[] args){
C1(N,M);
System.out.println(ans);
}
static int ans = 0;
//组合问题 从n个数中选择m个数
static void C1(int n,int m){
for(int i=m;i<=n;i++) {//不断选择第i(m <=i<=n)个元素作为每个组合的最后元素,
b[m-1] = i-1;
if(m>1)//重复步骤
C1(i-1,m-1);//i-1和m-1很关键
else {//若m等于1(对应b[0]),则表示选完,输出该组合(数组b中存储的是组合的元素在a中的下标)
int [][] map = new int[3][4];
int [][] book = new int[3][4];
int startx = 0,starty = 0;
for(int j=0;j<=M-1;j++){
System.out.print(a[b[j]]+" ");
if (a[b[j]]%4==0){
map[a[b[j]]/4-1][3] = 1;
startx = a[b[j]]/4-1;
starty = 3;
}else {
map[a[b[j]]/4][a[b[j]]%4-1] = 1;
startx = a[b[j]]/4;
starty = a[b[j]]%4-1;
}
}
if (bfs(startx,starty,map,book)){
ans++;
}
System.out.println();
}
}
}
/**
*变相的来判断图的连通性
*/
public static Boolean bfs(int startx,int starty,int [][] map,int [][] book){
System.out.println("startx="+startx+" starty="+starty);
int [][] next = {{-1,0},{1,0},{0,-1},{0,1}};
Queue<Node1> queue = new LinkedList<>();
queue.add(new Node1(startx,starty));
book[startx][starty] = 1;
List<Node1> list = new ArrayList<Node1>();
while(!queue.isEmpty()){
Node1 head = queue.poll();
list.add(head);
System.out.println(list.toString());
for (int i = 0; i < 4; i++) {
int x = head.x+next[i][0];
int y = head.y+next[i][1];
if (x<0||y<0||x>2||y>3) continue;
if (map[x][y]==1&&book[x][y]==0){
book[x][y]=1;
queue.offer(new Node1(x,y));
}
}
}
if (list.size()==5) {
System.out.println(list.size());
return true;
}
else {
System.out.println(list.size());
return false;
}
}
}
class Node1{
int x;
int y;
public Node1(int x, int y) {
this.x = x;
this.y = y;
}
@Override
public String toString() {
return "Node1{" +
"x=" + x +
", y=" + y +
'}';
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号